Дослідження стійкості, засноване на перетворенні одиничного круга в ліву напівплощину

Критерії Гурвіця, Льенара-Шипара і інші критерії стійкості безперервних систем дозволяють судити, знаходяться всі корені характеристичного рівняння в лівій напівплощині чи ні. Тому їх не можна безпосередньо використовувати для дослідження стійкості дискретних систем. Проте, очевидно, ними можна скористатися, якщо провести перетворення змінної характеристичного рівняння, при якому одиничний круг перетвориться в ліву напівплощину.

Твердження 22.1. При перетворенні

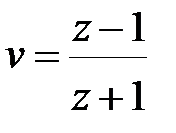
(22.7)

внутрішність одиничного круга на 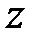-площині перетвориться в ліву напівплощину, його зовнішність – в праву напівплощину і коло (одиничного радіусу) – в уявну вісь на 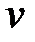-площини.

Доказ. Представимо комплексну змінну 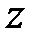у тригонометричній формі і підставимо в (22.7):

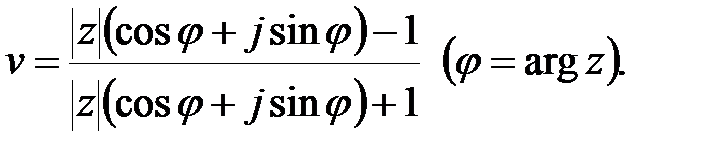
Перетворивши і розділивши вираз справа на дійсну і уявну частини, отримаємо

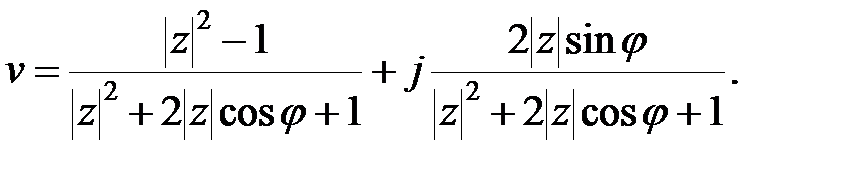
Так як 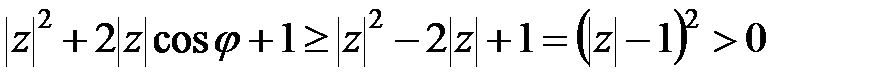при , то дійсна частина

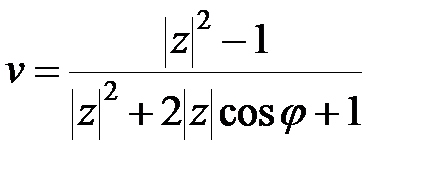
від’ємна при 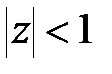, додатна при 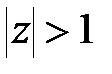і дорівнює нулю при 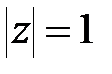. Отже, при перетворенні (22.7) внутрішність одиничного круга 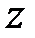-площини переходить в ліву напівплощину, а його зовнішня частина – в праву напівплощину 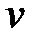-плоскости. Коло одиничного радіуса 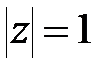переходить в уявну вісь. Дійсно, при

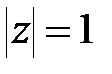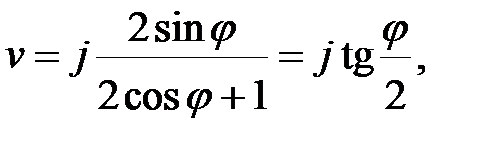
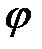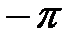і при зміні від до 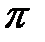змінна 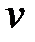змінює значення від 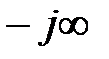до 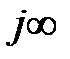Твердження доведене.

Вирішимо рівність (22.7) відносно 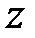і підставимо отриманий вираз в характеристичне рівняння (22.2):

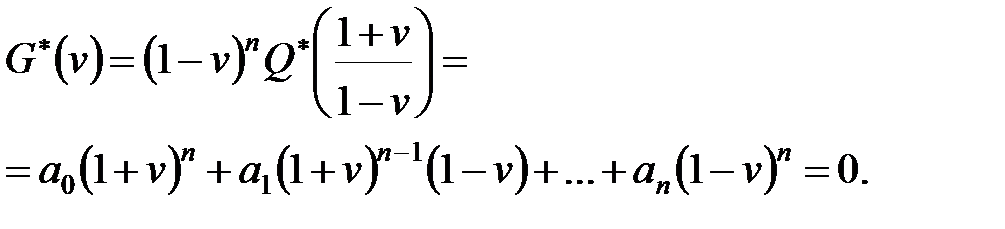
(22.8)

Представимо це перетворене характеристичне рівняння в стандартній формі:

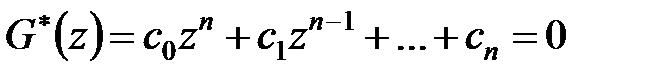
(22.9)

Вирази для коефіцієнтів цього рівняння через коефіцієнти початкового характеристичного рівняння отримаємо, якщо в (22.8) розкриємо дужки і проведемо приведення подібних членів, а потім прирівняємо коефіцієнти при однакових ступенях в (22.8) і (22.9).

Для 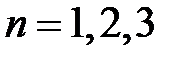маємо:

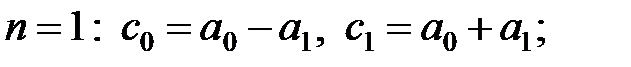
	(22.10а)
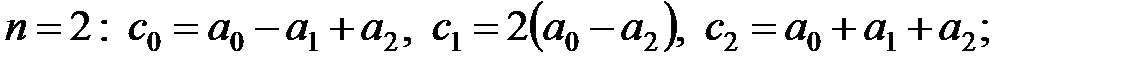
	(22.10б)
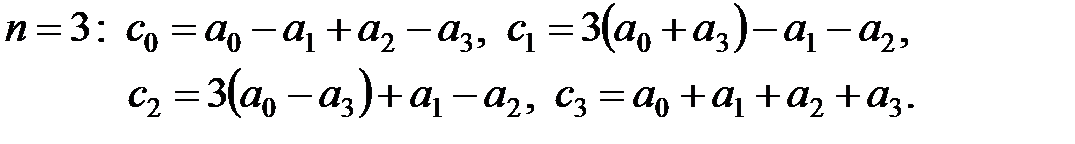
	(22.10в)

В силу твердження 22.1, якщо корені початкового характеристичного рівняння розташовується усередині одиничного круга, то корені перетвореного характеристичного рівняння (22.9) розташовується в лівій напівплощині.

Таким чином, для того, щоб дискретна система була стійка, необхідно і достатньо, щоб все корені перетвореного характеристичного рівняння (22.9) розташовувалося в лівій напівплощині (мали від’ємну дійсну частину).

Приклад 22.3. Характеристичний поліном дискретної системи управління має вигляд

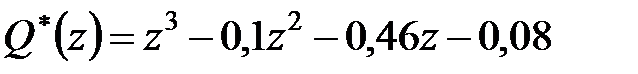. Визначити її стійкість.

Рішення. В даному випадку

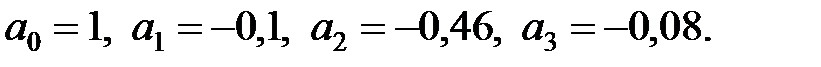
і відповідно до (22.10 в) коефіцієнти перетвореного рівняння рівні

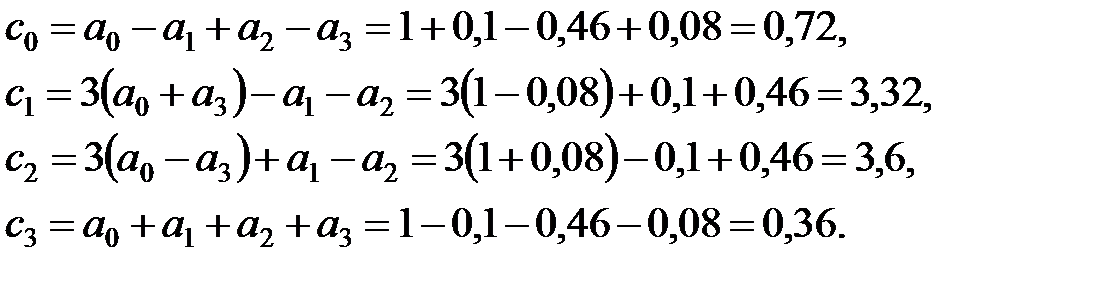
Необхідна умова стійкості виконується: всі коефіцієнти перетвореного характеристичного рівняння більше нуля. Визначник Гурвіця 2-го порядку є

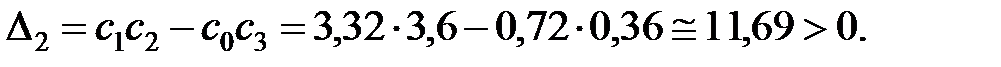
Отже, система стійка.