ЛЕКЦІЯ 23 ЧАСТОТНІ критерії стійкості
Розглянемо поліном, який отримується з характеристичного полінома 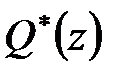 при підстановці в нього
при підстановці в нього  :
:

| (23.1) |
Цей поліном є характеристичним поліномом в 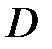 -зображеннях. Встановимо, якими повинні бути нулі
-зображеннях. Встановимо, якими повинні бути нулі 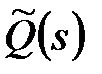 (тобто корені характеристичного рівняння
(тобто корені характеристичного рівняння 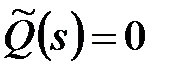 у
у 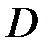 -зображеннях), щоб система була стійка.
-зображеннях), щоб система була стійка.
Представимо змінну 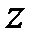 у вигляді
у вигляді 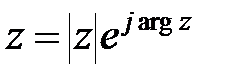 . Підставивши цей вираз в
. Підставивши цей вираз в  і прологарифмувавши, отримаємо
і прологарифмувавши, отримаємо

| (23.2) |
Оскільки 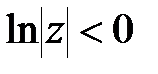 при
при  то умова стійкості дискретних систем
то умова стійкості дискретних систем 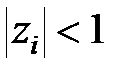
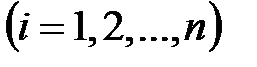 приймає вигляд
приймає вигляд

| (23.3) |
Таким чином, для того, щоб дискретна система була стійка, необхідно і достатньо, щоб всі корені її характеристичного рівняння в 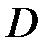 -зображеннях розташувалися в лівій
-зображеннях розташувалися в лівій 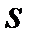 -напівплощині.
-напівплощині.
Через рівність 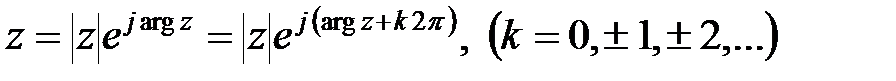 якщо
якщо 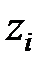 є коренем характеристичного рівняння
є коренем характеристичного рівняння 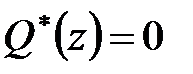 , то число
, то число
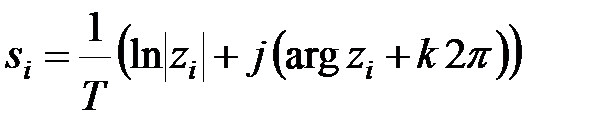
буде коренем характеристичного рівняння в 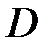 -зображеннях при любих
-зображеннях при любих 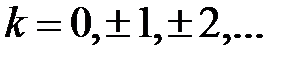 Інакше кажучи, характеристичне рівняння в
Інакше кажучи, характеристичне рівняння в 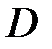 -зображеннях має нескінченну безліч рішень.
-зображеннях має нескінченну безліч рішень.
Корені  у яких уявна частина
у яких уявна частина 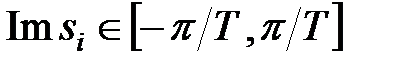 називатимемо основними коренями характеристичного рівняння в
називатимемо основними коренями характеристичного рівняння в 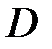 -зображеннях. Число основних коренів дорівнює ступеню характеристичного рівняння. Оскільки неосновні корені відрізняється від відповідних основних тільки уявною частиною, для дослідження стійкості досить розглянути тільки основні корені.
-зображеннях. Число основних коренів дорівнює ступеню характеристичного рівняння. Оскільки неосновні корені відрізняється від відповідних основних тільки уявною частиною, для дослідження стійкості досить розглянути тільки основні корені.
Принцип аргумента
Якщо 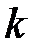 основних нулів характеристичного полінома
основних нулів характеристичного полінома
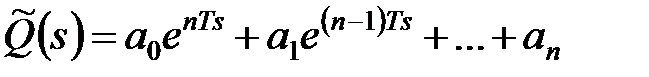 , ,
|
розташовані в лівій напівплощині, а останні 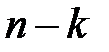 основних нулів – в правій напівплощині, той приріст
основних нулів – в правій напівплощині, той приріст 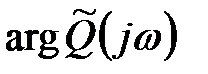 при зміні
при зміні 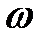 від
від 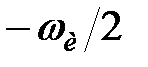 до
до 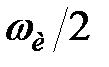
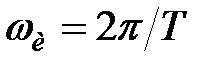
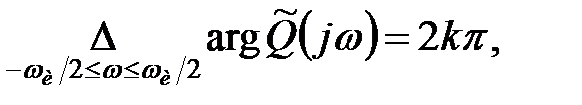
| (23.4) |
а при зміні 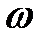 від 0 до
від 0 до 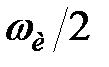 дорівнює
дорівнює 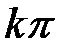 :
:
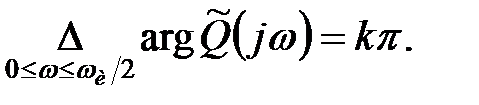
| (23.5) |
Доказ. Хай 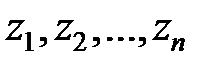 – нулі характеристичного полінома
– нулі характеристичного полінома 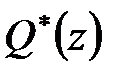 , а
, а 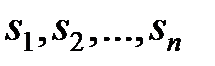 – нулі характеристичного полінома
– нулі характеристичного полінома 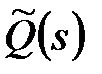 . Тоді ці поліноми можна представити у вигляді добутку
. Тоді ці поліноми можна представити у вигляді добутку
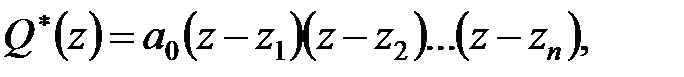
| (23.6) |
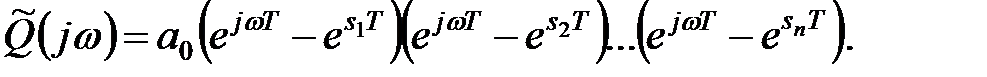
| (23.7) |
При 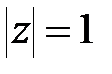 поклавши в (23.2)
поклавши в (23.2) 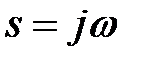 отримаємо
отримаємо 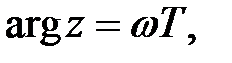 і відповідно
і відповідно 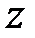 можемо представити у вигляді
можемо представити у вигляді 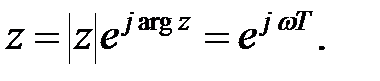
Цей вектор при зміні 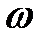 від
від 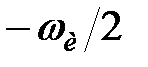 до
до 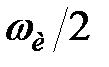 робить на
робить на 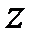 -площини повний оборот в додатному напрямку (проти руху годинникової стрілки), і його кінець описує коло одиничного радіусу. При цьому вектор
-площини повний оборот в додатному напрямку (проти руху годинникової стрілки), і його кінець описує коло одиничного радіусу. При цьому вектор 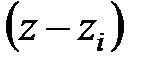
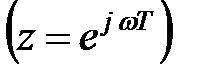 робить повний оборот щодо кінця вектора
робить повний оборот щодо кінця вектора 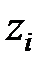 у додатному напрямку, і зміна його аргументу дорівнює
у додатному напрямку, і зміна його аргументу дорівнює 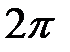 (рис. 23.1, а), якщо
(рис. 23.1, а), якщо 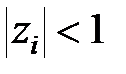 і зміна аргументу цього вектора дорівнює нулю, якщо
і зміна аргументу цього вектора дорівнює нулю, якщо 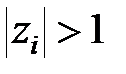 (рис. 23.1, б).
(рис. 23.1, б).

Рис. 23.1. До доказу принципу аргументу: 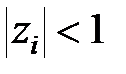 (а) і
(а) і 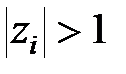 (б)
(б)
Тому
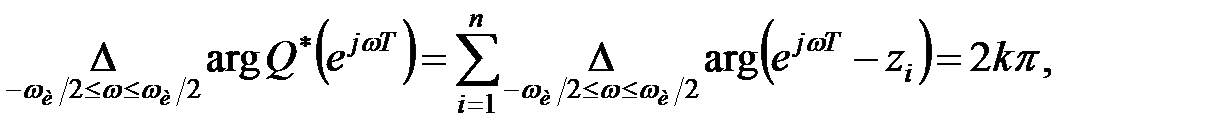
|
якщо 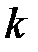 нулів полінома
нулів полінома 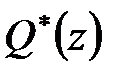 знаходяться усередині одиничного круга, а останні
знаходяться усередині одиничного круга, а останні 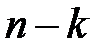 – поза одиничним кругом.
– поза одиничним кругом.
І так як 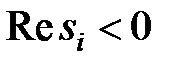 при
при 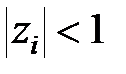 і
і 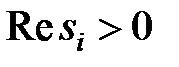 при
при 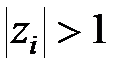 зміна аргументу
зміна аргументу 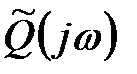 (див. (23.7)) визначається наступним чином:
(див. (23.7)) визначається наступним чином:
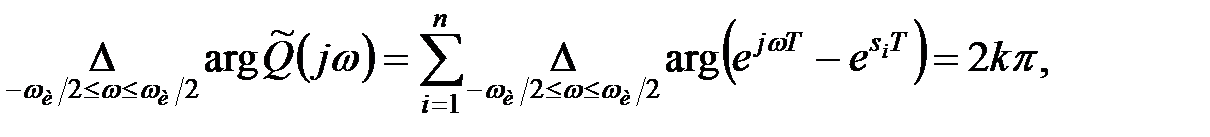
|
якщо 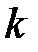 основних нулів характеристичного полінома
основних нулів характеристичного полінома 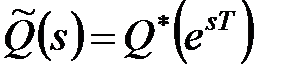 розташовані в лівій, а останні
розташовані в лівій, а останні 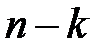 основних нулів – в правій
основних нулів – в правій 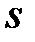 -напівплощині.
-напівплощині.
Тепер покажемо справедливість формули (23.5). Оскільки 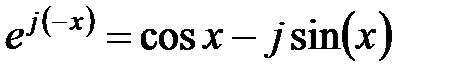 функція
функція 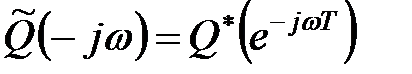 є комплексно-зв'язаною функцією
є комплексно-зв'язаною функцією  . Аргументи комплексно-зв'язаних функцій відрізняються тільки знаками:
. Аргументи комплексно-зв'язаних функцій відрізняються тільки знаками: 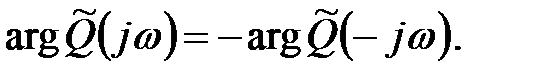
Звідси
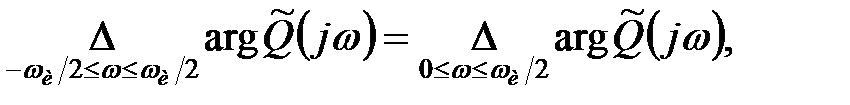
|
і з (23.4) отримуємо (23.5).
Критерій Найквіста
Для дослідження стійкості дискретних систем можна використовувати також критерій Найквіста (точніше, його аналог). Як і у разі безперервних систем, він використовується для визначення стійкості замкнутої системи по амплитудно-фазовій частотній характеристиці її розімкненої системи.
Хай передаточна функція дискретної системи управління в розімкненому стані має вигляд
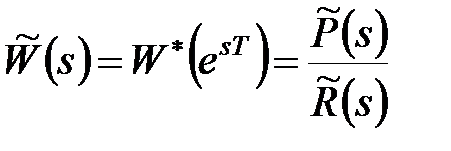 , ,
|
де 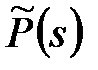 ,
, 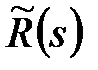 – поліноми від
– поліноми від 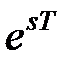 .
.
Критерій Найквіста. Якщо розімкнена система нестійка і її характеристичне рівняння 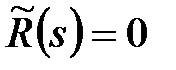 має
має 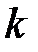 основних коренів в правій напівплощині і не містить коренів на уявній осі, то для того, щоб замкнута система була стійка, необхідно і достатньо, щоб амплітудно-фазова частотна характеристика розімкненої системи (годограф частотної передаточної функції
основних коренів в правій напівплощині і не містить коренів на уявній осі, то для того, щоб замкнута система була стійка, необхідно і достатньо, щоб амплітудно-фазова частотна характеристика розімкненої системи (годограф частотної передаточної функції 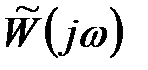 при зміні частоти
при зміні частоти 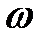 від 0 до
від 0 до 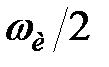 охоплювала точку
охоплювала точку 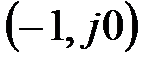
 раз.
раз.
Якщо розімкнена система стійка, то для того, щоб замкнута система була стійка, необхідно і достатньо, щоб амплітудно-фазова частотна характеристика розімкненої системи не охоплювала точку 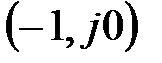 .
.
Доказ. Розглянемо функцію
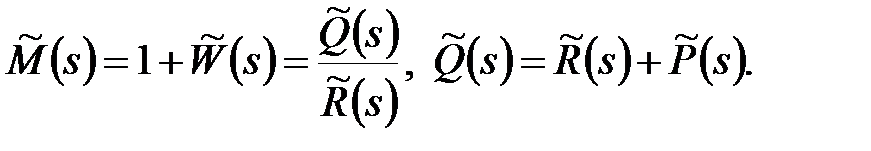
|
У чисельнику маємо характеристичний поліном замкнутої системи, а в знаменнику – характеристичний поліном розімкненої системи. Для того, щоб замкнута система була стійкою, необхідно і достатньо, щоб всі нулі характеристичного полінома замкнутої системи 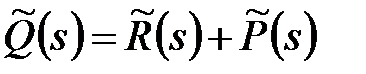 розташовувалися в лівій напівплощині або відповідно до принципу аргумента (див. (23.5)) виконувалася рівність
розташовувалися в лівій напівплощині або відповідно до принципу аргумента (див. (23.5)) виконувалася рівність 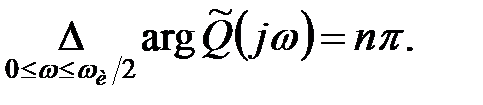
За умовою характеристичне рівняння 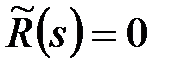 має
має 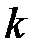 основних коренів в правій і останні
основних коренів в правій і останні 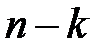 основних корені в лівій напівплощині. Тому відповідно до принципу аргументу
основних корені в лівій напівплощині. Тому відповідно до принципу аргументу
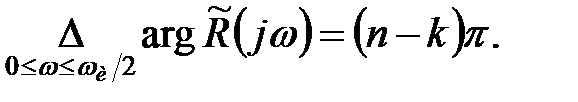
|
І так як 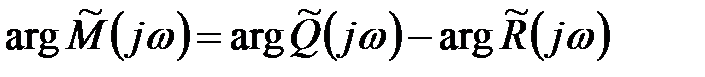 , то
, то
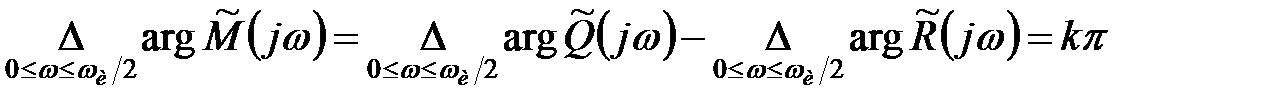 . .
|
Звідси слідує: для того, щоб замкнута система була стійка, необхідно і достатньо, щоб годограф вектора 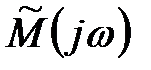 охоплював початок координат
охоплював початок координат 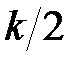 раз.
раз.
Через рівність 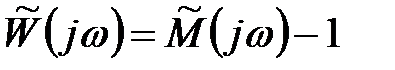 годограф
годограф 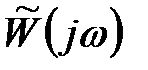 виходить з годографа
виходить з годографа  шляхом зрушення останнього вліво на одиницю (рис. 23.2). Тому для того, щоб замкнута система була стійка, необхідно і достатньо, щоб годограф вектора
шляхом зрушення останнього вліво на одиницю (рис. 23.2). Тому для того, щоб замкнута система була стійка, необхідно і достатньо, щоб годограф вектора 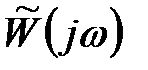 при зміні частоти
при зміні частоти 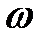 від 0 до
від 0 до 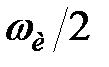 охоплював точку
охоплював точку 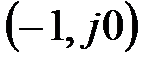
 раз.
раз.
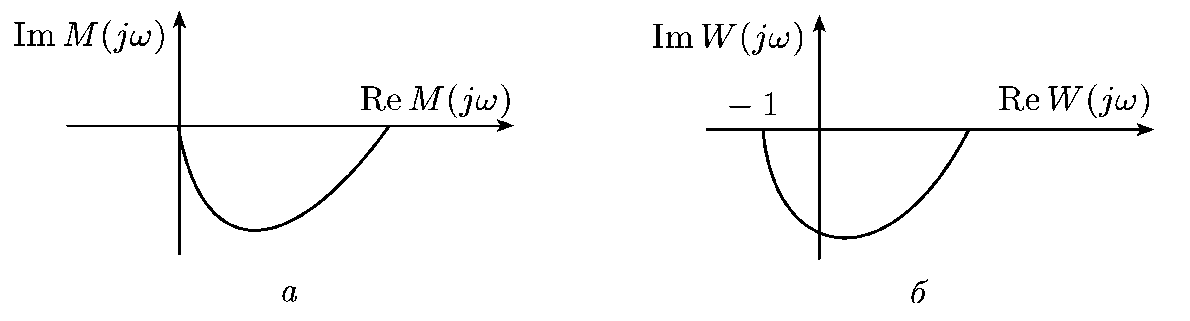
Рис. 23.2. До доказу критерію Найквіста:
а – годограф 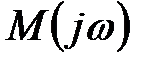 ; б – годограф
; б – годограф 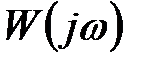
Якщо розімкнена система стійка, то 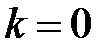 і для стійкості замкнутої системи необхідно і достатньо, щоб годограф
і для стійкості замкнутої системи необхідно і достатньо, щоб годограф 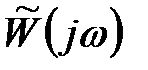 не охоплював точку
не охоплював точку 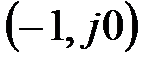 .
.
Приклад 23.1. Передаточна функція розімкненої системи
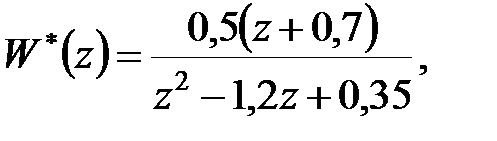 . .
|
період проходження імпульсів  Дослідити стійкість замкнутої системи.
Дослідити стійкість замкнутої системи.
Рішення. Визначимо стійкість по критерію Найквіста.
Частотна передаточна функція розімкненої системи визначається таким чином:
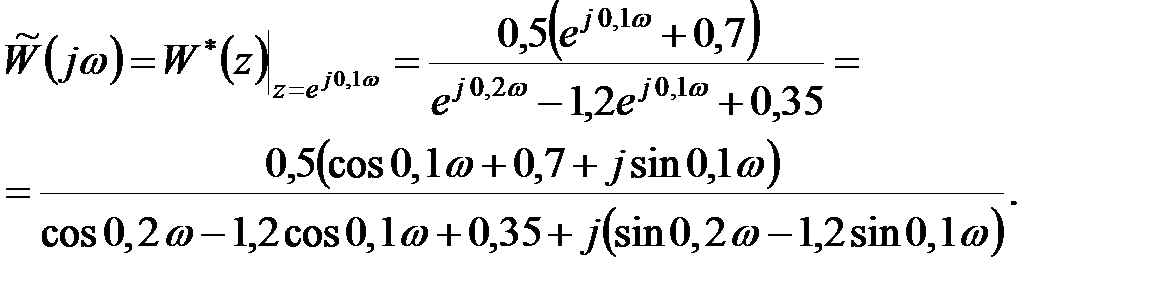 . .
|
Ввівши позначення
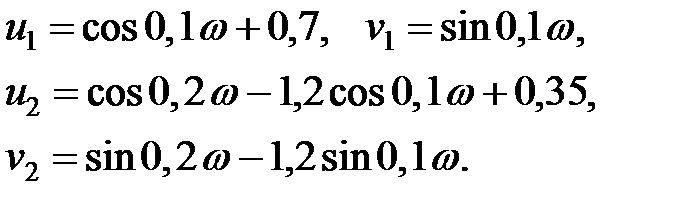
|
випишемо окремо дійсну і уявну частини:
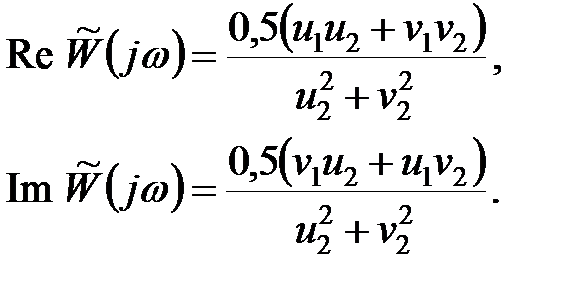
|
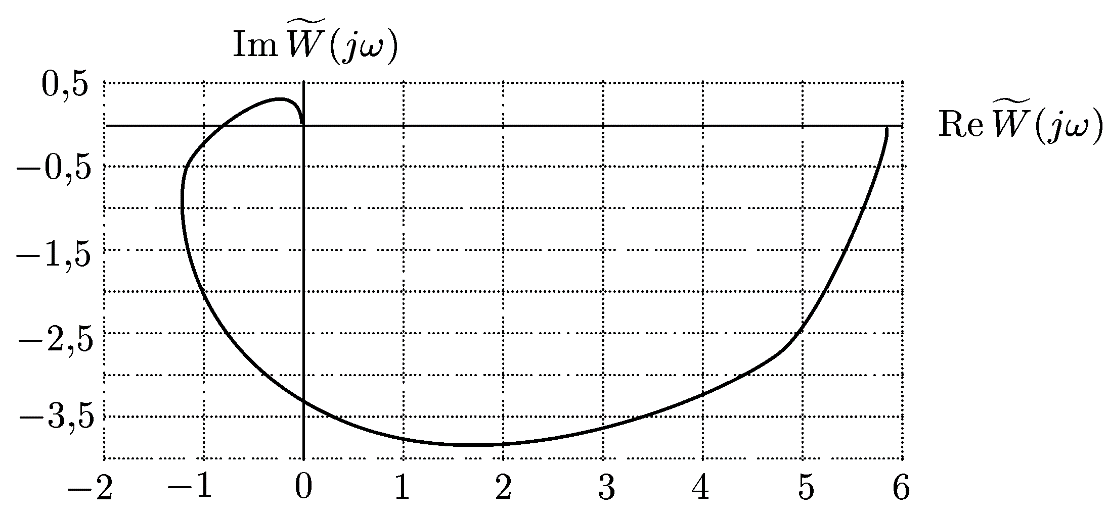
Рис. 23.3. АФЧХ
Амплітудно-фазова частотна характеристика (рис. 23.3) не охоплює точку  Розімкнена система стійка, оскільки нулі
Розімкнена система стійка, оскільки нулі 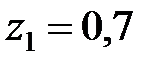 і
і 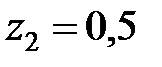 характеристичного полінома розімкненої системи
характеристичного полінома розімкненої системи 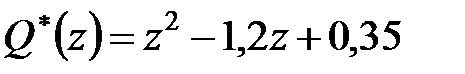 по модулю менше одиниці.
по модулю менше одиниці.
Отже, замкнута система стійка.
Дата добавления: 2017-08-01; просмотров: 335;
