Прямі показники якості
Серед прямих показників найчастіше використовуються час регулювання і перерегулювання. Нагадаємо: часом регулювання 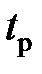 називається мінімальний час, після закінчення якого відхилення перехідної характеристики від сталого значення
називається мінімальний час, після закінчення якого відхилення перехідної характеристики від сталого значення 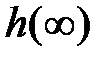 не перевищує заданої величини
не перевищує заданої величини  (рис. 24.1). Зазвичай приймають
(рис. 24.1). Зазвичай приймають 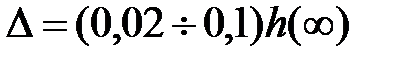 .
.
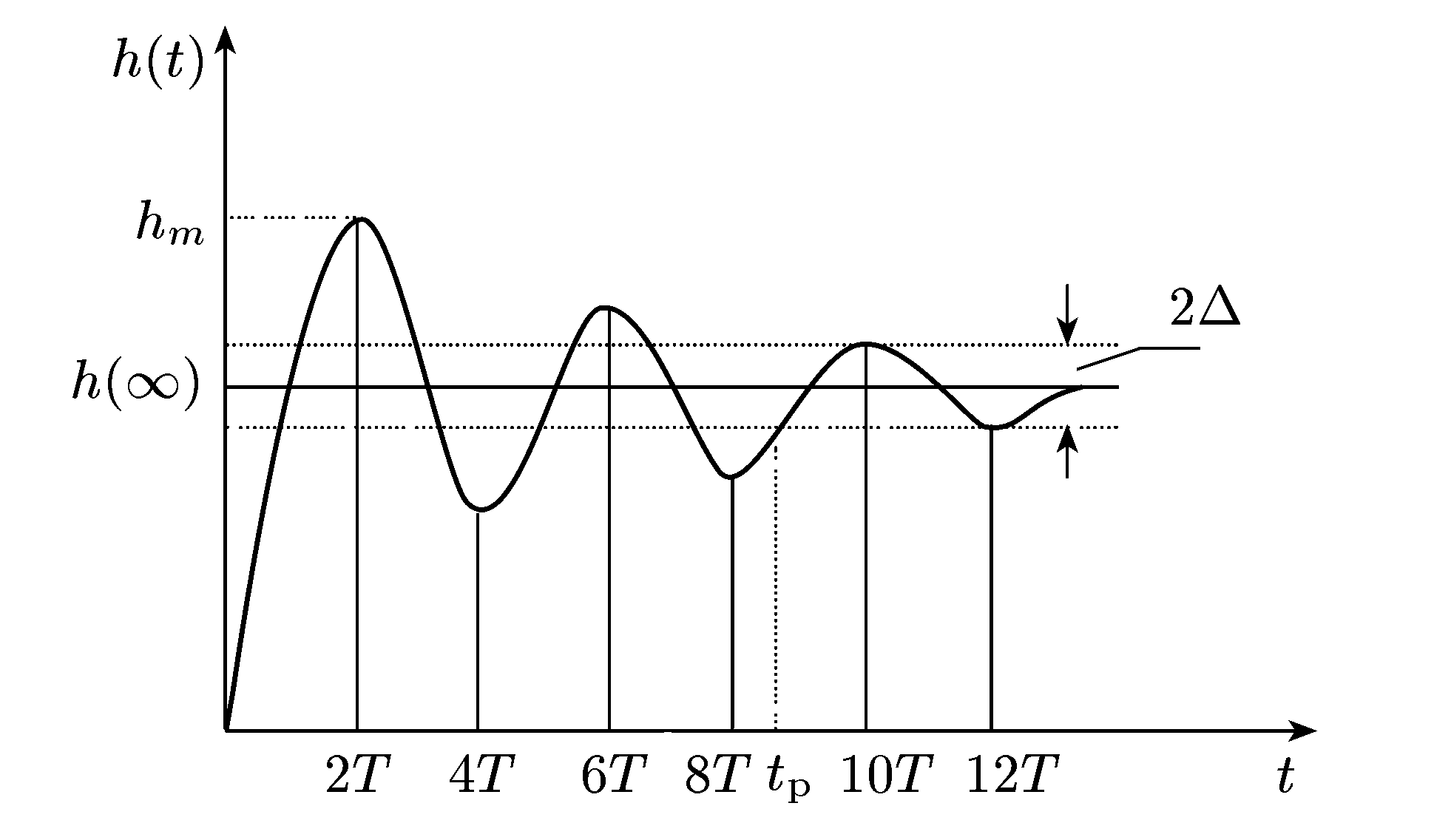
Рис. 24.1. Перехідна характеристика
Перерегулюванням 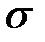 називають максимальне відхилення перехідної характеристики від сталого значення, виражене у відсотках до сталого значення:
називають максимальне відхилення перехідної характеристики від сталого значення, виражене у відсотках до сталого значення:
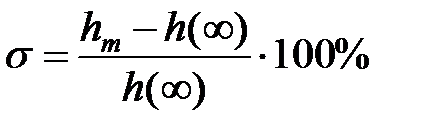 . .
|
Для графічного визначення прямих показників якості необхідно мати перехідну характеристику. Її можна побудувати по дискретній перехідній функції 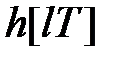 , сполучаючи дискретні точки плавної кривої.
, сполучаючи дискретні точки плавної кривої.
Розглянемо обчислення перехідної функції. За визначенням перехідна функція 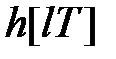 є функція, яка описує реакцію системи на одиничну дію
є функція, яка описує реакцію системи на одиничну дію  за нульових початкових умов. І так як
за нульових початкових умов. І так як 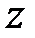 -зображення від одиничної гратчастої функції має вигляд
-зображення від одиничної гратчастої функції має вигляд 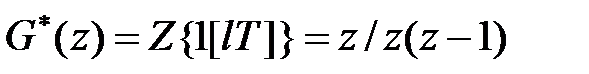
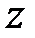
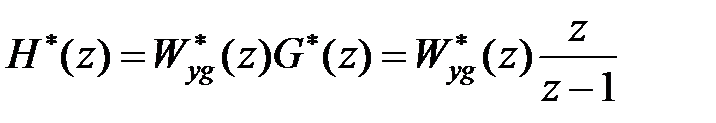 , ,
|
де  – передаточна функція щодо входу
– передаточна функція щодо входу 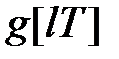 і виходу
і виходу 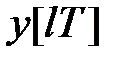 .
.
Зображення перехідної функції є відношення поліномів:
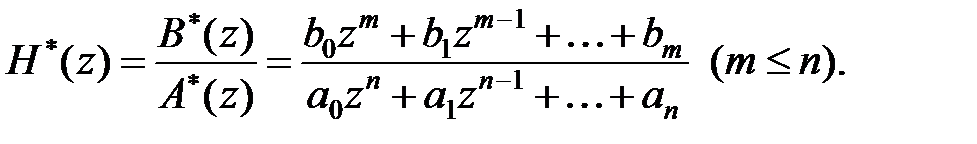
|
З іншого боку, за визначенням 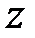 -перетворення
-перетворення
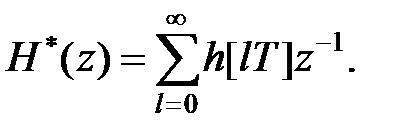
|
Тому значення перехідної функції 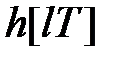 можна знайти, розклавши
можна знайти, розклавши 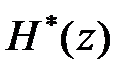 у ряд Лорана шляхом ділення чисельника
у ряд Лорана шляхом ділення чисельника 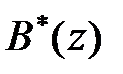 на знаменник
на знаменник 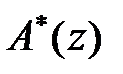 за правилом ділення многочленів. При цьому в многочленах
за правилом ділення многочленів. При цьому в многочленах 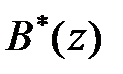 і
і 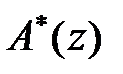 доданки повинні розташовуватися в порядку убування ступеня
доданки повинні розташовуватися в порядку убування ступеня 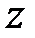 .
.
Приклад 24.1. Визначити значення перехідної функції 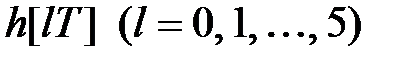 дискретної системи з передаточною функцією
дискретної системи з передаточною функцією
 . .
|
Рішення. 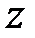 -зображення перехідної функції має вигляд
-зображення перехідної функції має вигляд
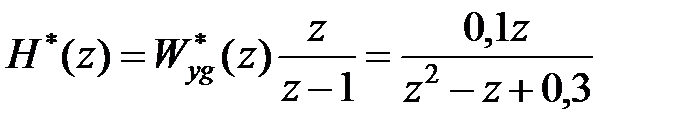 , ,
|
Провівши ділення чисельника на знаменник за правилом ділення многочленів, для перших п'яти доданків отримаємо
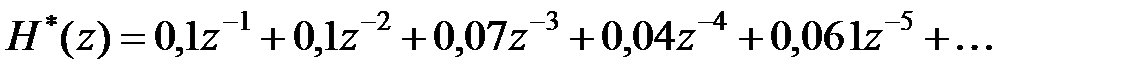 , ,
|
Звідси маємо  ,
, 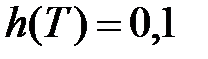 ,
, 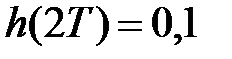 ,
, 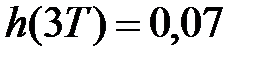 ,
, 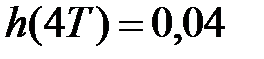 ,
, 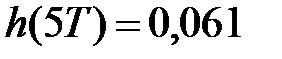 .
.
Якщо різниця між ступенями знаменника і чисельника дорівнює 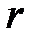 , то перший член розкладання
, то перший член розкладання  у ряд Лорана буде мати ступінь
у ряд Лорана буде мати ступінь 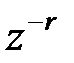 . Тому перші
. Тому перші 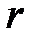 значень
значень 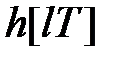 будуть дорівнювати нулю:
будуть дорівнювати нулю:
 . .
|
Інший спосіб обчислення перехідної функції заснований на формулі розкладання, яка визначається таким чином: якщо всі полюси 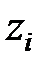
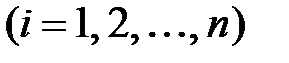 функції
функції  (тобто корені рівняння
(тобто корені рівняння 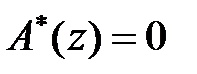 ) прості і не дорівнюють нулю, то [6]
) прості і не дорівнюють нулю, то [6]
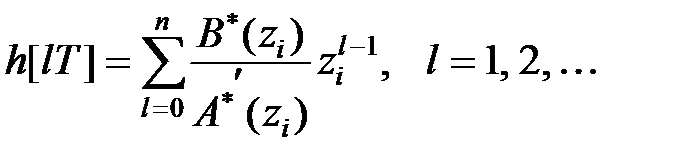 , ,
| (24.1) |
де  .
.
Початкові значення: 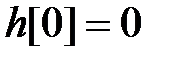 при
при 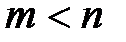 і
і  при
при 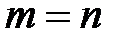 .
.
Приклад 24.2. Визначити перехідну функцію 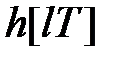 , якщо
, якщо 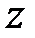 -зображення має вигляд
-зображення має вигляд  .
.
Рішення. В даному випадку  і
і  . Похідна є
. Похідна є 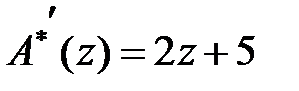 , полюсами є
, полюсами є 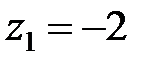 і
і 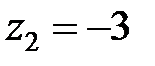 і відповідно до формули (24.1)
і відповідно до формули (24.1)
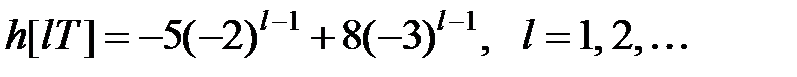 . .
|
Початкове значення 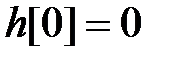 , оскільки ступінь чисельника менше ступеня знаменника.
, оскільки ступінь чисельника менше ступеня знаменника.
Якщо 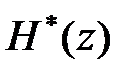 має кратні полюси, то полюсу
має кратні полюси, то полюсу  кратності
кратності 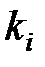 у формулі розкладання відповідає доданок, визначуваний граничним співвідношенням [6]
у формулі розкладання відповідає доданок, визначуваний граничним співвідношенням [6]
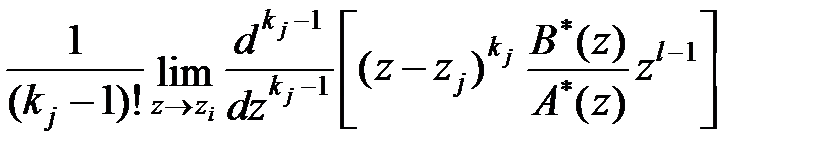 . .
| (24.2) |
Якщо серед полюсів 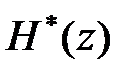 є нульовий полюс (
є нульовий полюс ( 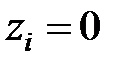 ), то при обчисленні відповідного цьому полюсу доданку слід користуватися формулою (24.2) і у тому випадку, коли цей полюс є простим.
), то при обчисленні відповідного цьому полюсу доданку слід користуватися формулою (24.2) і у тому випадку, коли цей полюс є простим.
Приклад 24.3. Визначити перехідну функцію 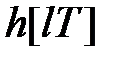 , якщо її
, якщо її  -зображення має вигляд
-зображення має вигляд 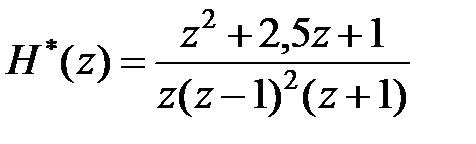 .
.
Рішення. В даному випадку 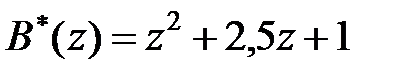 и
и  . Похідна є
. Похідна є 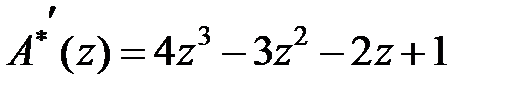 , полюси
, полюси 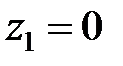 ,
, 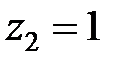 и
и  . Доданок, відповідний нульовому полюсу (
. Доданок, відповідний нульовому полюсу ( 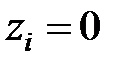 ), відповідно до формули (24.2) визначається таким чином:
), відповідно до формули (24.2) визначається таким чином:
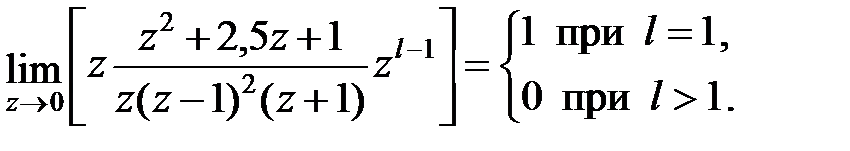
|
Полюс 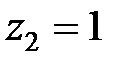 має кратність 2, і йому відповідає доданок
має кратність 2, і йому відповідає доданок
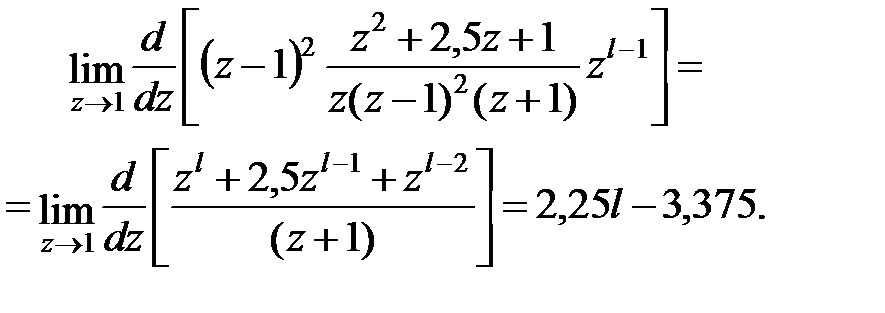
|
Полюс  є простим, і йому відповідає доданок (див. (24.1))
є простим, і йому відповідає доданок (див. (24.1))
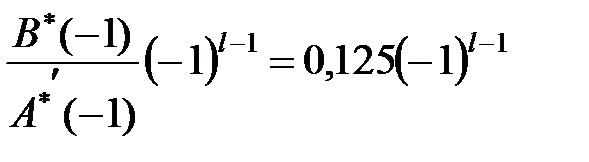 . .
|
Таким чином, маємо
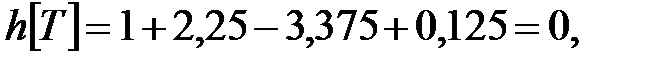
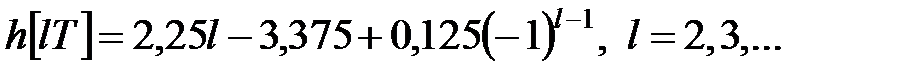
|
Початкове значення: 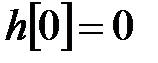 .
.
Обчислення перехідної функції між точками знімання сигналів. Функція 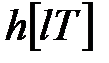 визначає значення перехідної функції в моменти знімання сигналу
визначає значення перехідної функції в моменти знімання сигналу 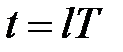
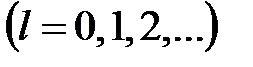 . При необхідності можна отримати функцію
. При необхідності можна отримати функцію 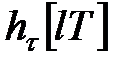 , яка визначає значення перехідної функції в проміжні моменти часу
, яка визначає значення перехідної функції в проміжні моменти часу  ,
, 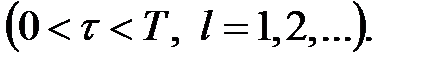
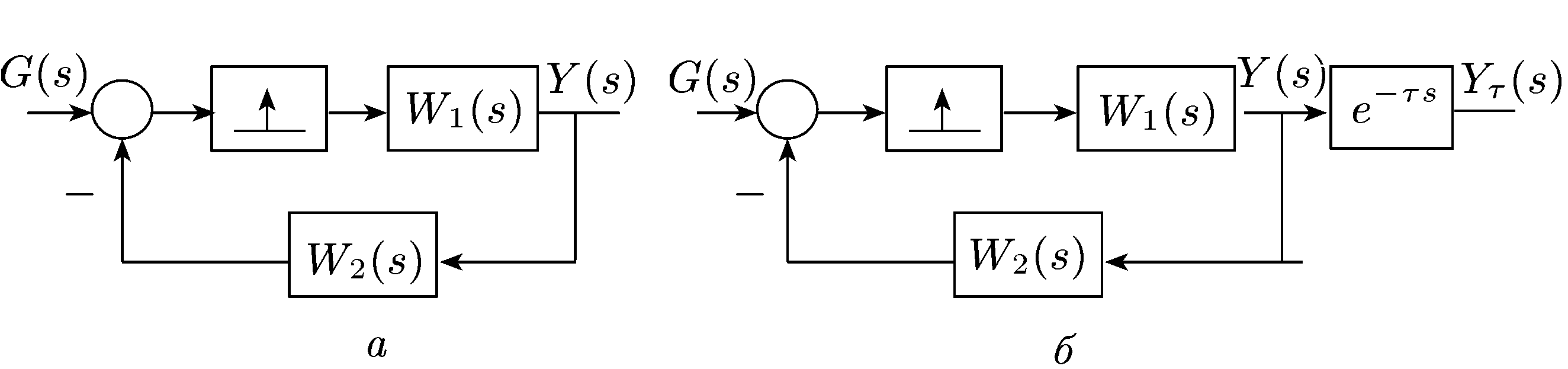
Рис. 24.2. Структурні схеми (до визначення перехідної функції 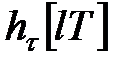 ):
):
а – початкова схема; б – перетворена схема
Для цього розглянемо структурну схему (рис. 24.2, б), яка виходить з початкової (рис. 24.2, а) підключенням на виході ланки чистого запізнювання.
З цих схем маємо

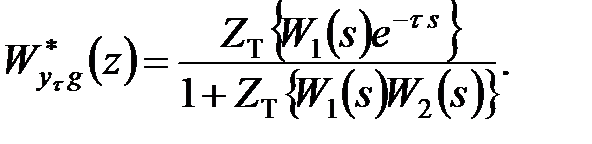
|
Оскільки  і при одиничній вхідній дії і нульових початкових умовах
і при одиничній вхідній дії і нульових початкових умовах 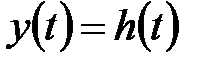 і
і  то
то 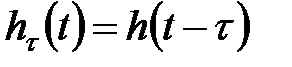 . Відповідно для
. Відповідно для  -зображень перехідних функцій
-зображень перехідних функцій 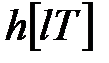 і
і 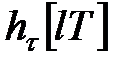 маємо
маємо
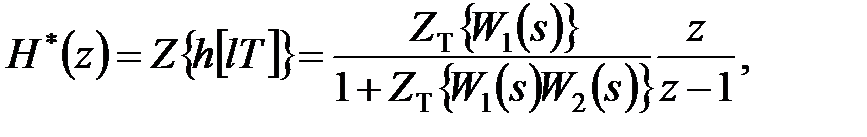
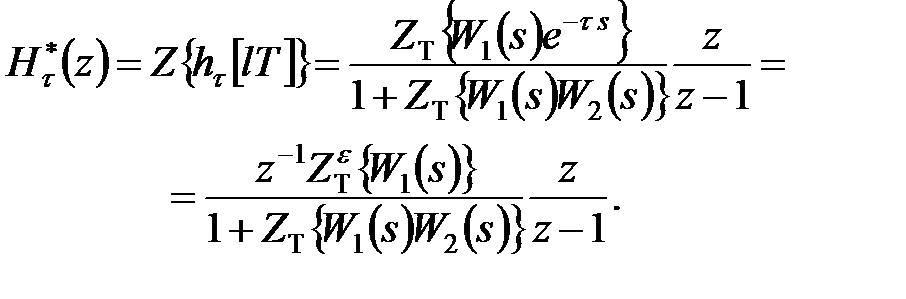
| (24.3) |
де  .
.
Приклад 24.4. Нехай в дискретній системі (см. рис. 24.2, а) 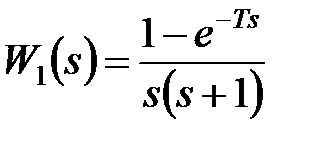 ,
, 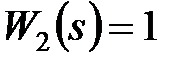 , і період проходження імпульсів
, і період проходження імпульсів 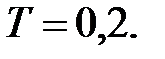 Потрібно визначити гратчасту функцію, яка приймає значення перехідної функції
Потрібно визначити гратчасту функцію, яка приймає значення перехідної функції 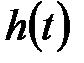 у моменти
у моменти 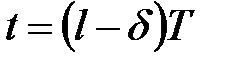 де
де 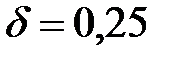
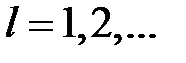
Рішення. Шуканою функцією буде 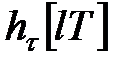 де
де 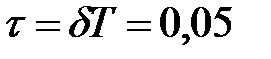 . В даному випадку
. В даному випадку 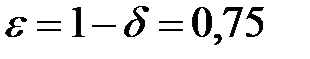 і
і
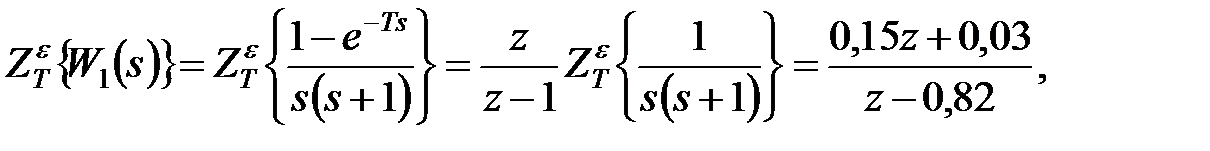

|
Підставивши ці вирази в (24.3), отримаємо
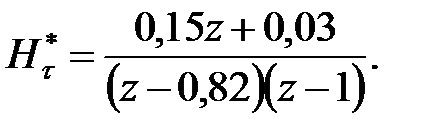
|
Звідси відповідно до формули (24.1)
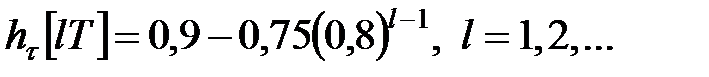
|
Дата добавления: 2017-08-01; просмотров: 226;
