Обчислення коефіцієнтів помилок
Обчислювати коефіцієнти помилки за формулою (25.3) незручно. Тому зазвичай використовують формули, що зв'язують коефіцієнти помилки з передаточною функцією помилки 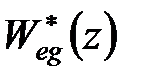 і що мають наступний вигляд:
і що мають наступний вигляд:
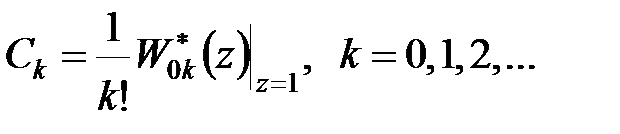
| (25.4) |
Тут 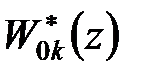 визначається за рекурентною формулою
визначається за рекурентною формулою
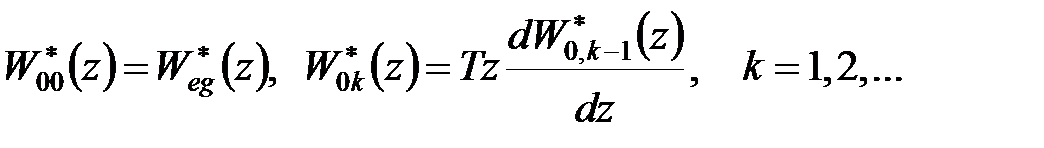
| (25.5) |
З приведених формул виходить, що коефіцієнт позиційної помилки 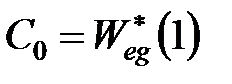 і для знаходження решти коефіцієнтів необхідно обчислювати похідні від передаточної функції
і для знаходження решти коефіцієнтів необхідно обчислювати похідні від передаточної функції 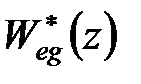 . Проте, якщо коефіцієнти помилки
. Проте, якщо коефіцієнти помилки 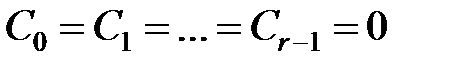 і
і 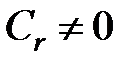 то всі ці коефіцієнти, включаючи перший відмінний від нуля коефіцієнт, можна обчислити, не знаходячи похідні.
то всі ці коефіцієнти, включаючи перший відмінний від нуля коефіцієнт, можна обчислити, не знаходячи похідні.
Доведемо справедливість приведених формул.
Формула (25.4) буде справедлива, тобто матиме вигляд (25.3), якщо
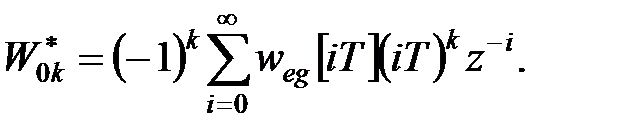
| (25.6) |
Справедливість цієї формули покажемо методом математичної індукції.
Враховуючи, що передаточна функція 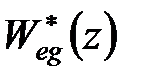 і вагова функція
і вагова функція 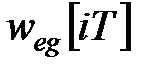 помилки зв'язані співвідношенням
помилки зв'язані співвідношенням
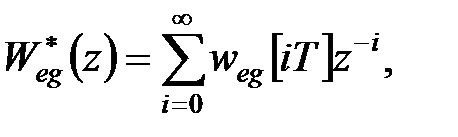
|
відповідно до (25.5) при 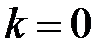 маємо
маємо
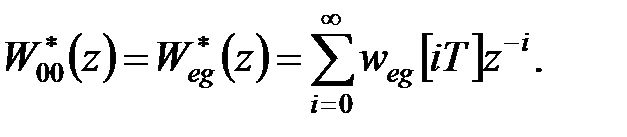
|
Звідси витікає, що формула (25.6) при 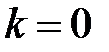 справедлива.
справедлива.
Допустимо, що вона справедлива при 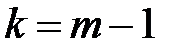 :
:
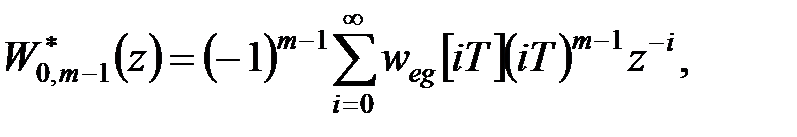
|
або
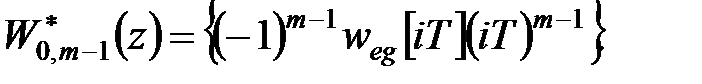
|
Покажемо, що вона справедлива і при 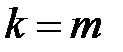 . Відповідно до формули (25.5)
. Відповідно до формули (25.5)
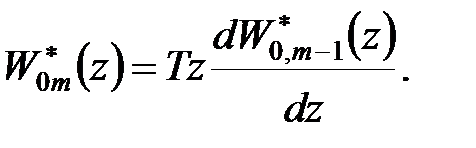
| (25.5) |
Звідси, враховуючи прийняту вище формулу для 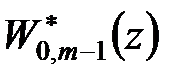 і властивість
і властивість 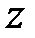 -перетворення про множення оригіналу на
-перетворення про множення оригіналу на 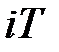 отримуємо
отримуємо
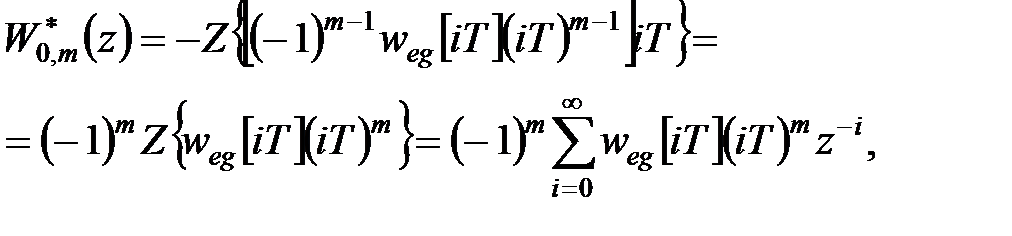
|
що і доводить справедливість формули (25.6) при 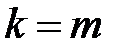 .
.
Приклад 25.1. Передаточна функція помилки 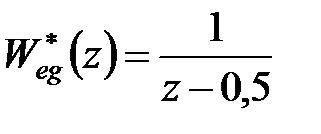 , період
, період 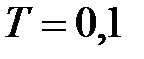 . Визначити коефіцієнти помилки
. Визначити коефіцієнти помилки 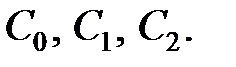
Рішення. Згідно формул (25.4) і (25.5) маємо
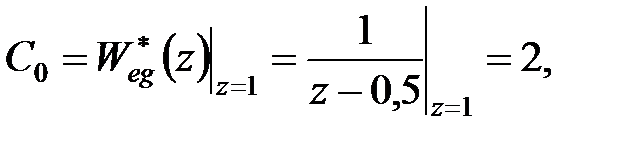
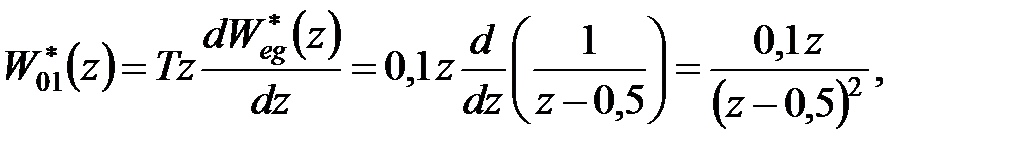
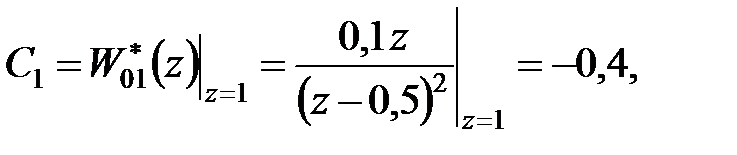
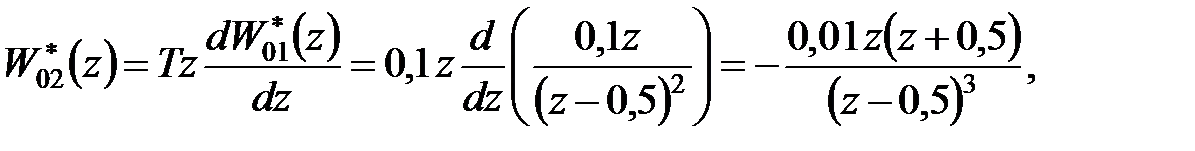
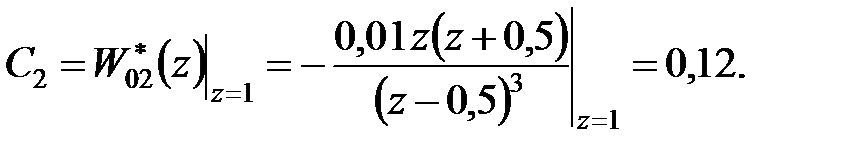
|
Дата добавления: 2017-08-01; просмотров: 236;
