Особливості перехідного процесу дискретних систем
У безперервних лінійних системах перехідна функція завжди приймає стале значення при 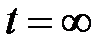 . Проте можливі лінійні дискретні системи, в яких перехідний процес закінчується за кінцеве число кроків, тобто існує таке додатне число
. Проте можливі лінійні дискретні системи, в яких перехідний процес закінчується за кінцеве число кроків, тобто існує таке додатне число  що
що
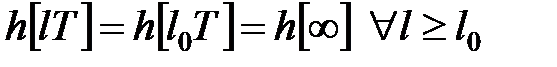 . .
| (24.4) |
Якщо виконується умова (24.4), то перехідний процес називається оптимальним, а система, в якій відбувається такий процес, називається оптимальною (по перехідному процесу) системою.
Умова оптимальності системи (по перехідному процесу). Переходячи до оригіналів, з рівності
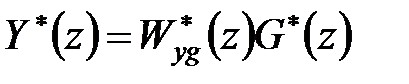 , ,
|
по теоремі про згортання отримаємо
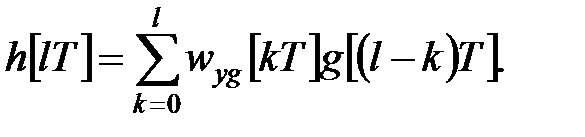
| (24.5) |
За визначенням перехідної функції при 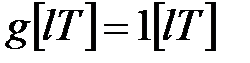 з (24.5) маємо
з (24.5) маємо
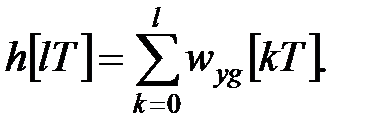
| (24.6) |
Звідси витікає, що система буде оптимальною по перехідному процесу, тобто буде виконано умову (24.4), якщо
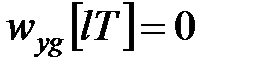 при при 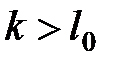
| (24.7) |
При виконанні цієї умови передаточна функція, пов'язана з ваговою функцією 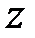 -перетворенням, приймає вигляд
-перетворенням, приймає вигляд
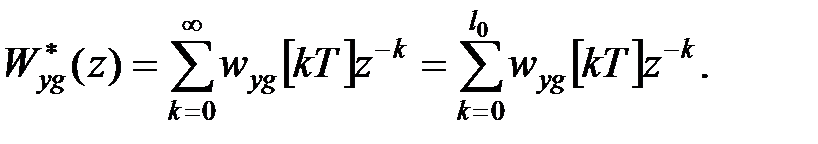
| (24.8) |
У загальному випадку передаточна функція 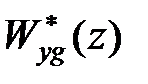 є відношенням поліномів:
є відношенням поліномів:
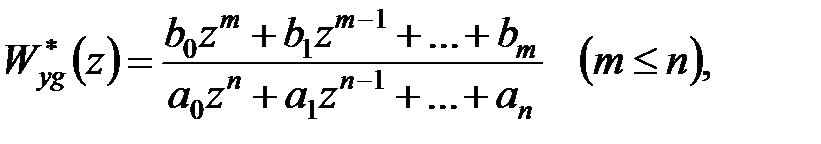
| (24.9) |
і вона при розкладанні в ряд Лорана прийме вигляд (24.8), якщо
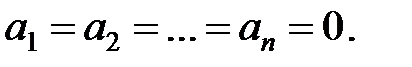
| (24.10) |
Дійсно, в цьому випадку маємо

|
Таким чином, система (24.9) є оптимальною (перехідний процес в ній закінчується за кінцеве число кроків), якщо виконується умова (24.10).
Приклад 24.5. Замкнута дискретна система складається з фіксатора нульового порядку і безперервної частини з передаточною функцією  період
період  . Визначити параметр
. Визначити параметр 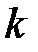 , при якому перехідний процес буде оптимальним.
, при якому перехідний процес буде оптимальним.
Рішення. При фіксаторі нульового порядку передаточна функція формуючої ланки має вигляд 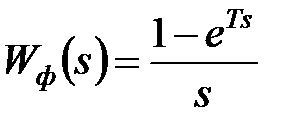 . Тому передаточна функція приведеної безперервної частини має вигляд
. Тому передаточна функція приведеної безперервної частини має вигляд
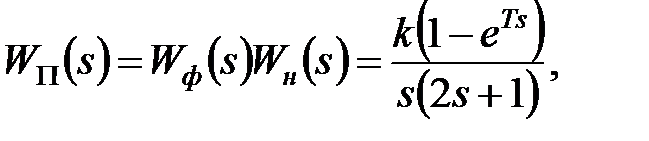
|
і передаточна функція розімкненої дискретної моделі дорівнює

|
Передаточна функція замкнутої системи має вигляд
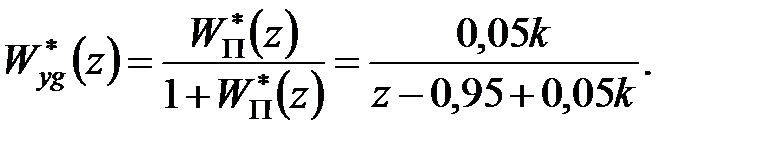
|
Звідси відповідно до формули (24.10) для оптимального  отримуємо
отримуємо 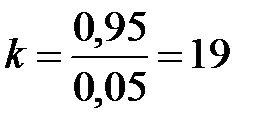 .
.
Дата добавления: 2017-08-01; просмотров: 209;
