Вплив квантування за часом на стійкість

Розглянемо вплив дискретизації за часом на стійкість на прикладі АІМ-системи, що складається з фіксатора нульового порядку і безперервної частини спочатку з передаточною функцією 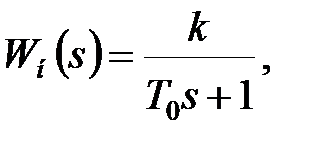а потім з 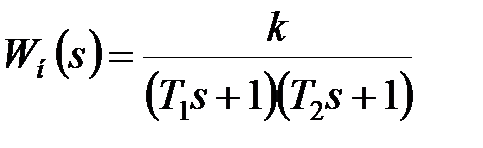. Система без дискретного елементу, тобто безперервна система, стійка при будь-якому додатному 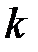у обох випадках.

У першому випадку передаточна функція приведеної безперервної частини є

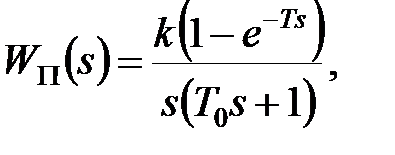
і дискретна передаточна функція розімкненої системи має вигляд

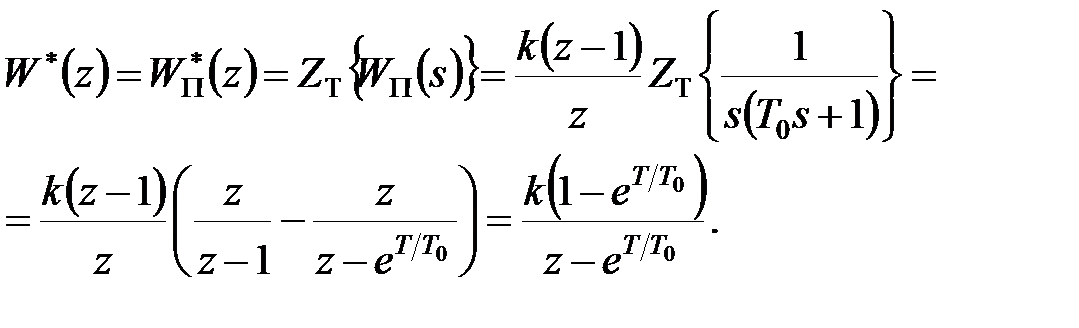
Звідси для характеристичного рівняння замкнутої системи маємо

.

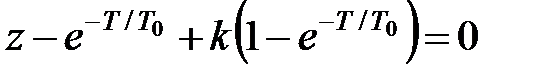Коефіцієнти перетвореного характеристичного рівняння дорівнюють

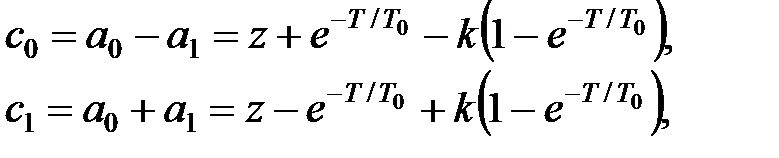
і умова стійкості приймає вигляд

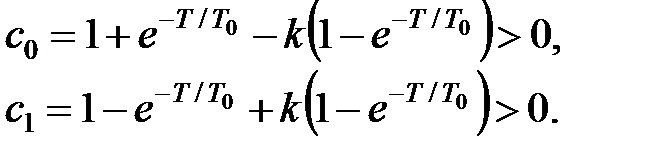
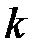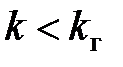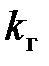Друга нерівність виконується при будь-якому додатному , а перша – тільки при де – граничний передаточний коефіцієнт системи, визначуваний з умови :

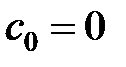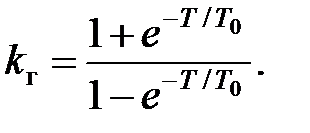
При малому періоді 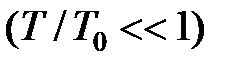, поклавши 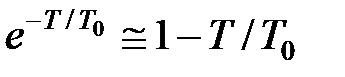отримаємо

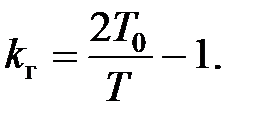
(23.8)

З цієї рівності виходить: 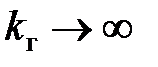при 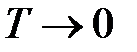. Проте при кінцевому періоді, яким би він не був малим, дискретна система стійка не при будь-якому передаточному коефіцієнті системи.

Тепер розглянемо випадок, коли передаточна функція безперервної частини має вигляд

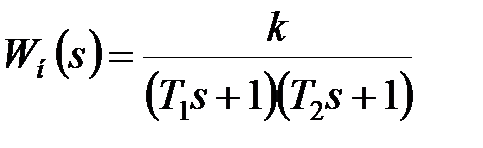
і дискретна передаточна функція розімкненої системи має вигляд

.

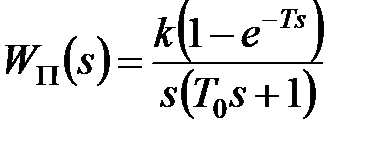Передаточна функція приведеної безперервної частини є

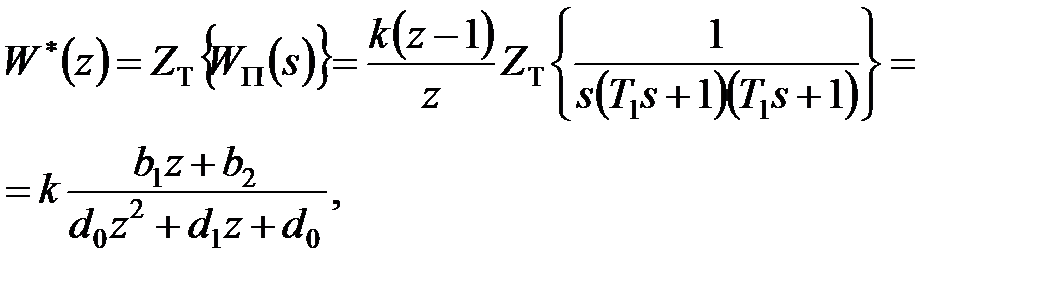
де

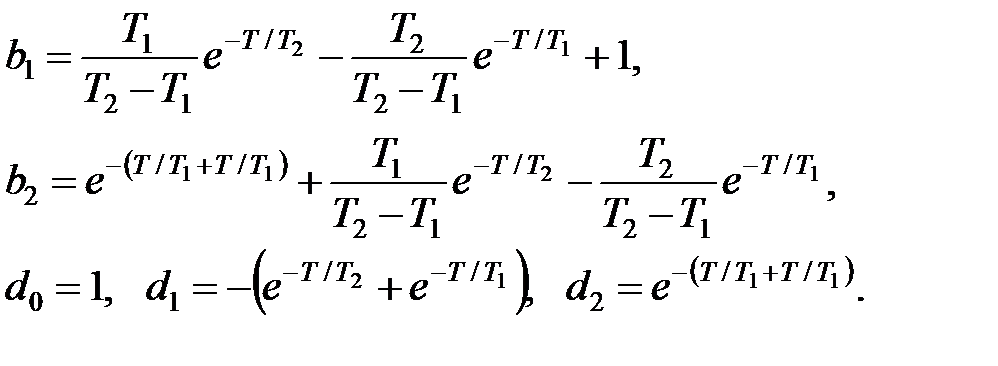
При малому періоді 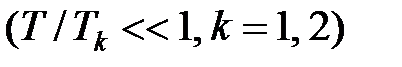, скориставшись виразом 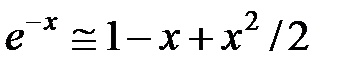отримаємо

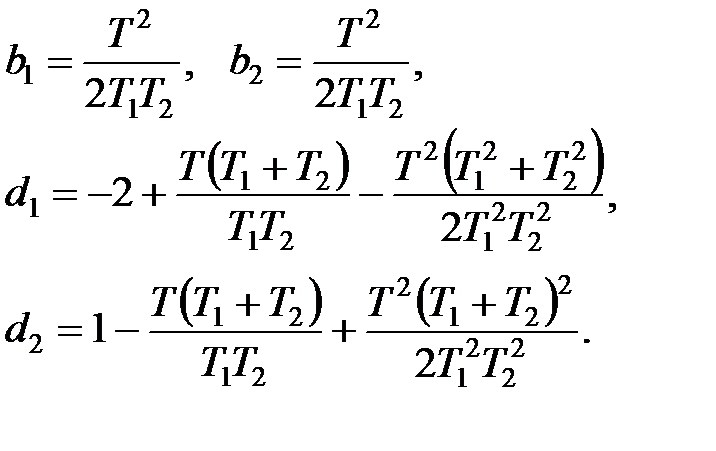
Характеристичне рівняння замкнутої системи має вигляд

.

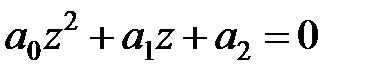де

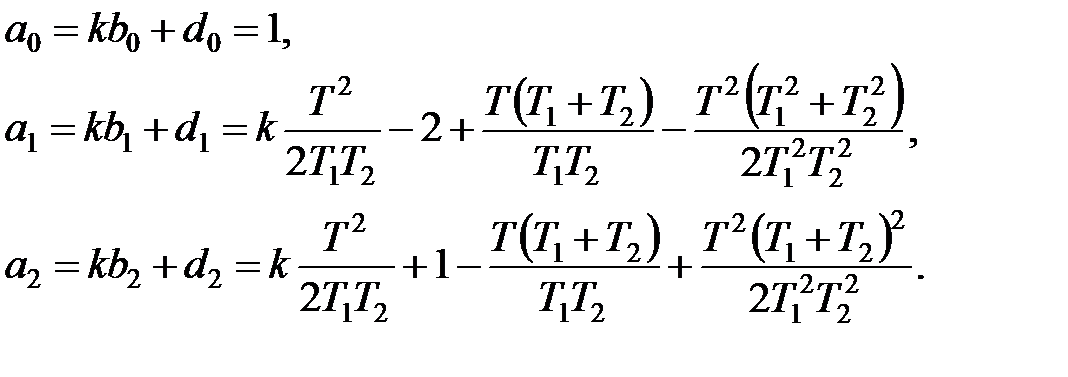
Коефіцієнти перетвореного характеристичного рівняння і умова стійкості мають вигляд

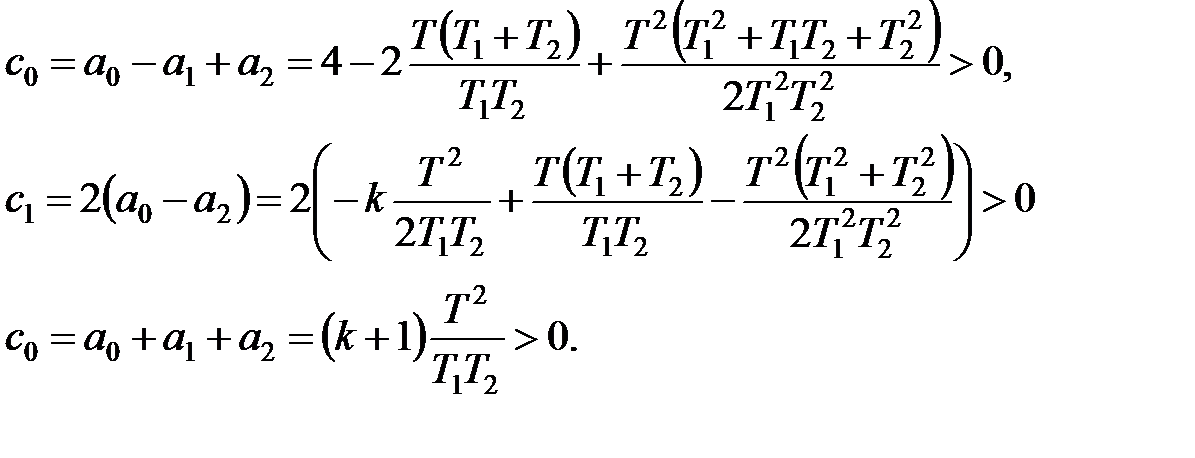
Перша і третя нерівності виконуються при будь-якому додатному передаточному коефіцієнті 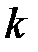друга – тільки при 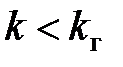, де граничний передаточний коефіцієнт

.

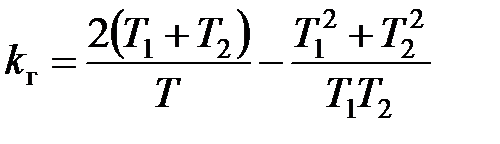(23.9)

З формули (23.9) виходить: 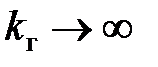при .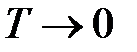

Отже, дискретизація за часом може привести до нестійкості навіть системи 1-го і 2-го порядку. При цьому, як і слід було чекати, граничний передаточний коефіцієнт із зменшенням періоду квантування збільшується і прагне до нескінченності з наближенням періоду до нуля.