Критерій стійкості Джурі

Складемо таблицю Джурі, яка містить 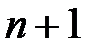рядків і стільки ж стовпців. При цьому заповнені клітки мають трикутну форму: нульовий рядок містить 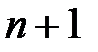заповнених клітин, а все подальші рядки мають на одиницю менше заповнених клітин, чим попередній рядок (табл. 22.1).

Таблиця 22.1. Таблиця Джурі

Клітини нульового рядка заповнюються коефіцієнтами характеристичного рівняння в порядку зростання нижніх індексів: 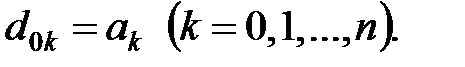Елементи першого рядка 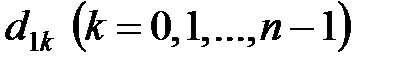обчислюються таким чином.

Виписуються елементи нульового рядка і під ними ті ж елементи в зворотному порядку. З елементів верхнього рядка віднімаються відповідні елементи нижнього рядка, помножені на відношення останніх елементів двох виписаних рядків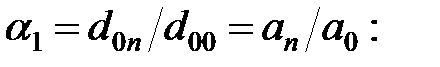

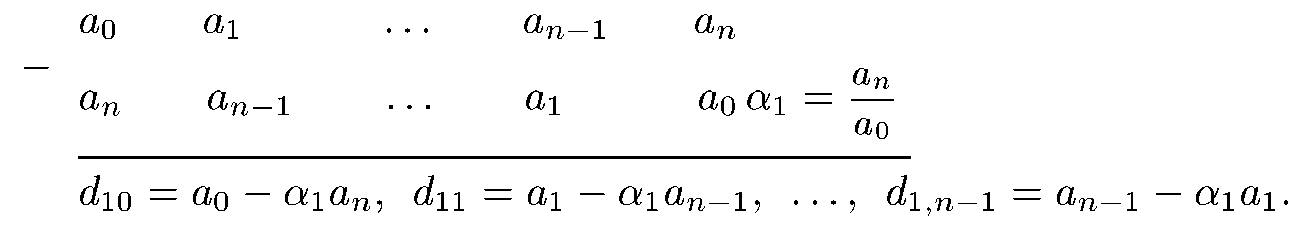
Остання різниця звертається в нуль, і вона відкидається. Тому перший рядок містить елементів: на один елемент менше, ніж нульовий рядок.

Елементи всіх подальших рядків визначаються аналогічно елементам першого рядка. Так, наприклад, для обчислення 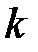-го рядка виписуються елементи 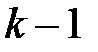-го рядка і під. ними ті ж елементи в зворотному порядку. З елементів верхнього рядка віднімаються відповідні елементи нижнього рядка, помножені на відношення останніх елементів виписаних двох рядків .

Остання різниця, що звертається в нуль, відкидається. Формула для обчислення 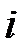-го елементу -го рядку 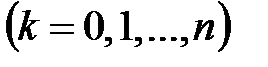має вигляд

, ,

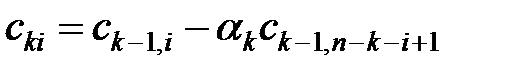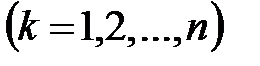(22.11)

Критерій Джурі (E.I. Jury). Для того, щоб всі нулі (корені) характеристичного полінома 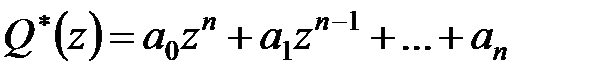знаходилися усередині одиничного круга, необхідно і достатньо, щоб при всі елементи нульового стовпця таблиці Джурі були додатні: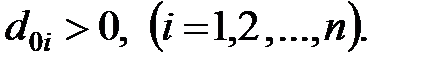

Якщо всі елементи нульового стовпця, окрім останнього, додатні: 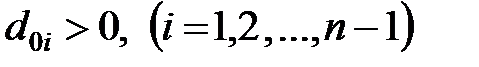, то додатність останнього елементу, тобто умова еквівалентна необхідній умові стійкості (22.5). Тому якщо необхідна умова виконується, то останній елемент 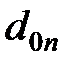можна не обчислювати.

Приклад 22.4. Характеристичний поліном дискретної системи управління має вигляд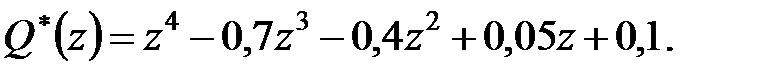

Дослідити стійкість даної системи.

Рішення. Спочатку перевіримо необхідну умову стійкості:

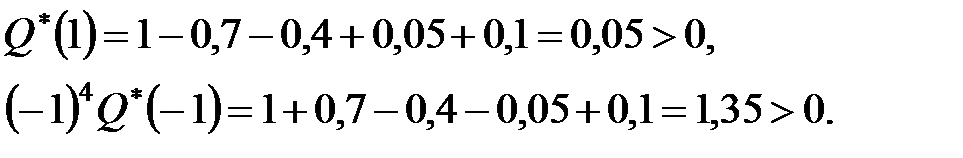
Необхідна умова стійкості виконується. Обчислимо елементи таблиці Джурі.

Для нульового рядка маємо

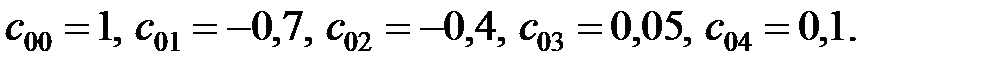
Нижче приводиться обчислення елементів таблиці Джурі для решти рядків, окрім останнього:

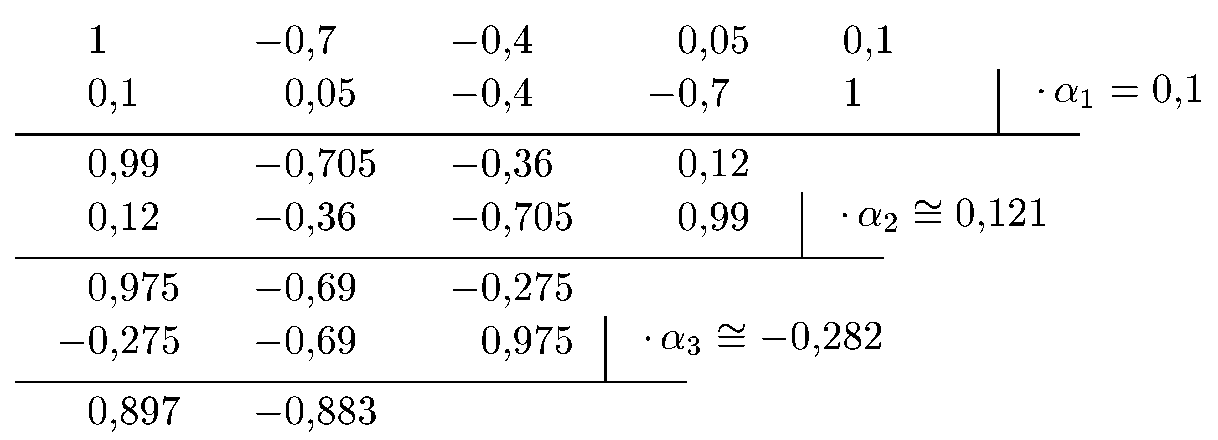
Елементи нульового стовпця (окрім останнього) дорівнюють відповідно 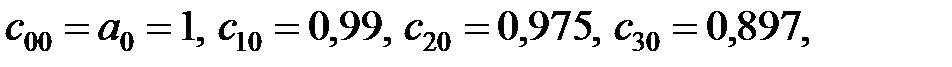і вони додатні. Оскільки виконується необхідна умова стійкості, останній елемент нульового стовпця також буде додатним. Отже, система стійка.