Алгебраїчні критерії стійкості

Тут ми розглянемо необхідну умову стійкості, визначення стійкості, засноване на перетворенні внутрішності одиничного круга в ліву напівплощину, і критерії стійкості Джурі.

Необхідна умова стійкості

Для того, щоб всі нулі (корені) характеристичного полінома

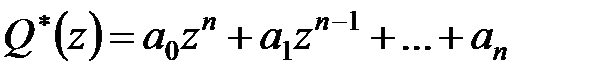
були по модулю менше одиниці 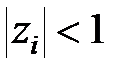необхідно, щоб при 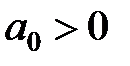виконувалися нерівності

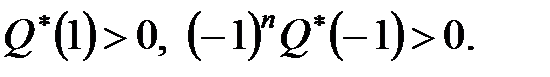
(22.5)

Щоб довести це твердження, розкладемо поліном 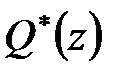на елементарні множники:

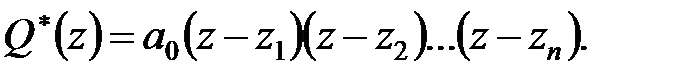
(22.6)

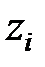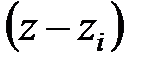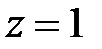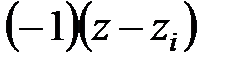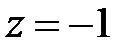Якщо корінь є дійсним і по модулю менше одиниці, то множник при і множник при будуть додатними. Якщо корінь 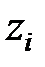є комплексним, тобто 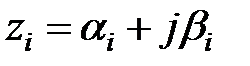( 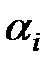, 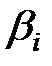– дійсні числа), то існує комплексно-зв'язаний корінь .

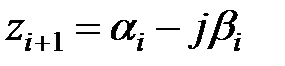Добуток 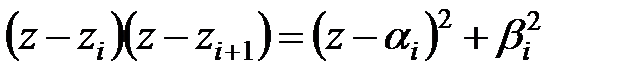при 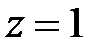і добуток 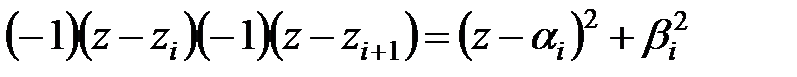при 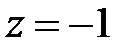будуть додатними. Отже, з (22.6) витікає, що якщо всі корені характеристичного полінома по модулю менше одиниці, то виконуватимуться нерівності (22.5).

Приклад 22.2. Характеристичний поліном дискретної системи має вигляд 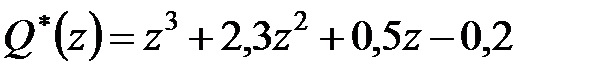. Потрібно визначити стійкість системи.

Рішення. Перевіримо необхідну умову стійкості. В даному випадку 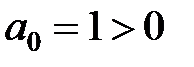і

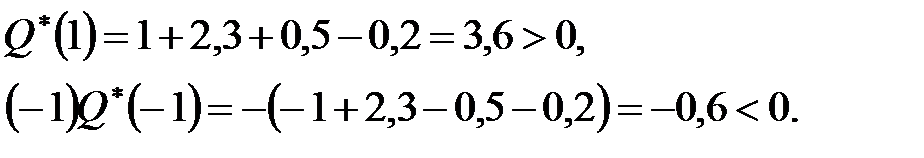
Необхідна умова стійкості не виконується. Отже, система нестійка.