Безперервна модель дискретної системи
Припустимо, що дискретна система складається з дискретного елементу (ДЕ) і безперервної частини (БЧ) (рис. 21.13, а).
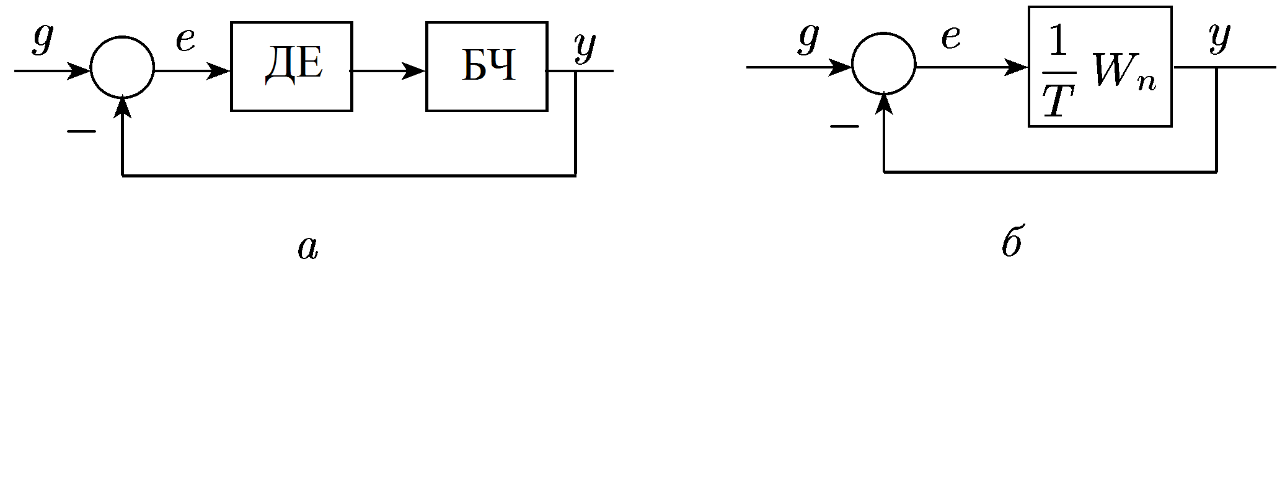
Рис. 21.13. Дискретна система (а) і її безперервна модель (б)
Дискретний елемент виробляє прямокутні імпульси з періодом 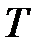 , відносною тривалістю
, відносною тривалістю 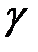 і амплітудою
і амплітудою 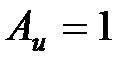 . Тоді передаточна функція приведеної безперервної частини має вигляд
. Тоді передаточна функція приведеної безперервної частини має вигляд
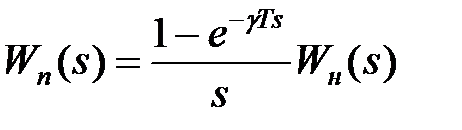 , ,
|
де 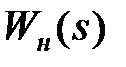 – передаточна функція безперервної частини.
– передаточна функція безперервної частини.
Враховуючи, що 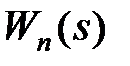 є зображення Лапласа вагової функції ПБЧ
є зображення Лапласа вагової функції ПБЧ 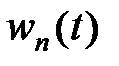 а передаточна функція в
а передаточна функція в 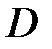 -зображеннях розімкненої дискретної системи –
-зображеннях розімкненої дискретної системи – 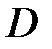 -зображення
-зображення 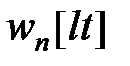 згідно з формулою (21.9) маємо
згідно з формулою (21.9) маємо
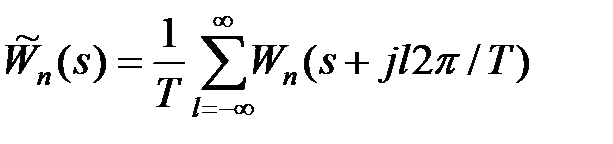 . .
|
Замінивши 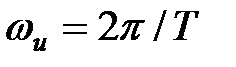 для частотної передаточної функції розімкненої дискретної системи отримуємо
для частотної передаточної функції розімкненої дискретної системи отримуємо
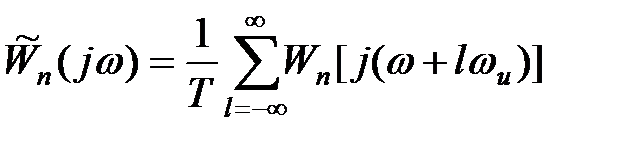 . .
| (21.10) |
Як наголошувалося вище, частотна передаточна функція 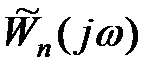 є періодичною функцією з періодом
є періодичною функцією з періодом 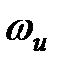 і при побудові частотних характеристик досить обмежитися інтервалом
і при побудові частотних характеристик досить обмежитися інтервалом 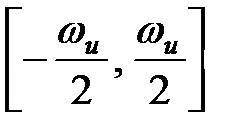 і якщо виконується умова
і якщо виконується умова
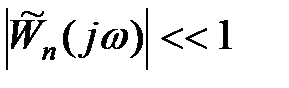 при при 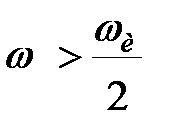 , ,
| (21.11) |
то у формулі (21.10) справа можна обмежитися одним доданкам, відповідним 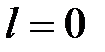 . Решта членів за вказаної умови не чинитиме істотного впливу на частотну характеристику. Тому за умови (21.11) можемо прийняти
. Решта членів за вказаної умови не чинитиме істотного впливу на частотну характеристику. Тому за умови (21.11) можемо прийняти
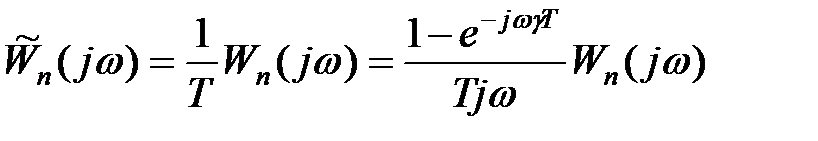 , ,
|
і початкову дискретну систему можна представити безперервною моделлю (рис. 21.13, б). При малих 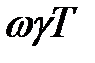
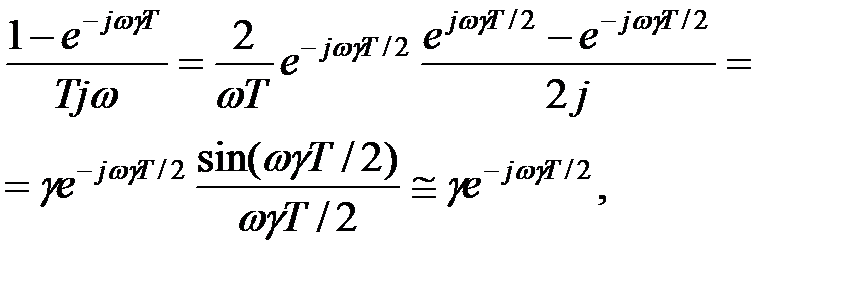
|
і передаточна функція розімкненої системи безперервної моделі має вигляд
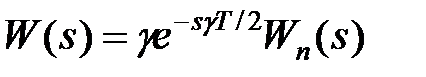 , ,
|
або, коли відносна тривалість 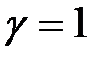 ,
,
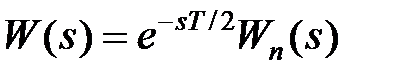 . .
| (21.12) |
Таким чином, дискретизація за часом відповідає введенню чистого запізнювання на півперіоду. При малих 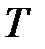 наявність дискретного елементу не враховують і приймають
наявність дискретного елементу не враховують і приймають
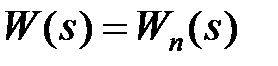 . .
| (12.13) |
Проте слід мати на увазі, що безперервна модель, заснована на останньому співвідношенні, може приводити до неправильних виводів.
Наприклад, коли безперервна частина є аперіодичною або коливальною ланкою, замкнута система виходить стійкою при будь-якому передаточному коефіцієнті, якщо виходити із співвідношення (12.13). Проте насправді через те, що дискретний елемент вносить запізнювання, існує максимальне значення передаточного коефіцієнта, вище за яке замкнута система буде нестійкою.
Дата добавления: 2017-08-01; просмотров: 356;
