Структура астатичних систем
Як було показано вище, система має астатизм 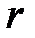 -го порядку, якщо передаточна функція помилки
-го порядку, якщо передаточна функція помилки  може бути представлена у вигляді
може бути представлена у вигляді
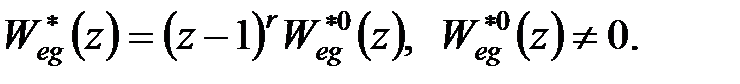
|
Оскільки передаточна функція помилки має вигляд
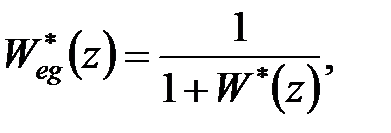
|
де 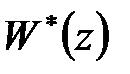 – передаточна функція розімкненої системи, то вона може бути представлена у вказаному вище вигляді, якщо передаточна функція
– передаточна функція розімкненої системи, то вона може бути представлена у вказаному вище вигляді, якщо передаточна функція 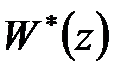 має вигляд
має вигляд
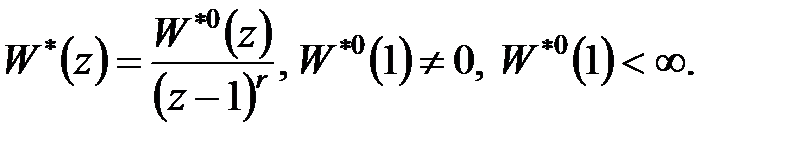
| (26.7) |
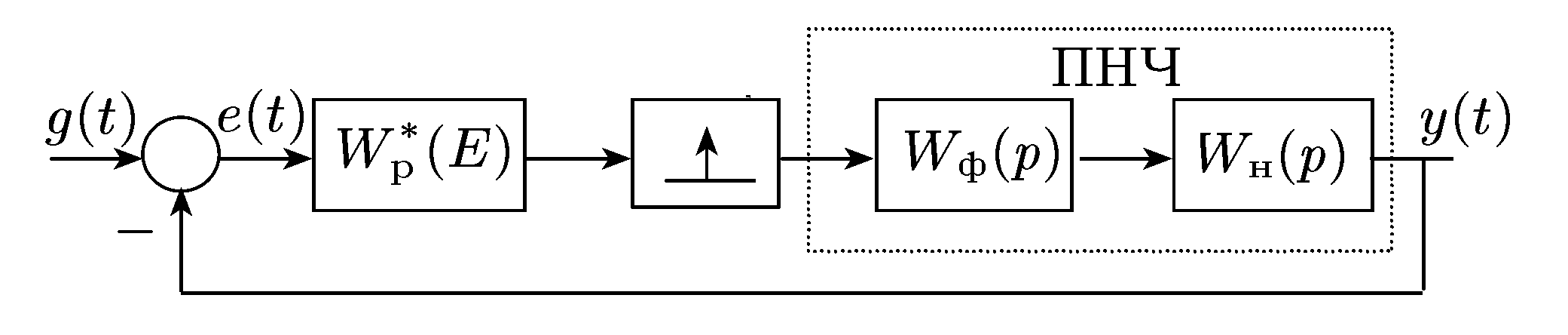
Рис. 26.1. Структурна схема дискретної системи
Припустимо, що дискретна система складається з дискретного фільтру (регулятора) і приведеної безперервної частини (рис. 26.1) Передаточна функція розімкненої системи має вигляд

|
де 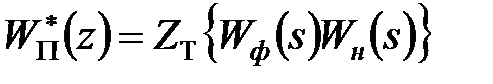 .
.
Система буде астатичною, якщо 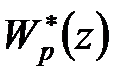 або
або 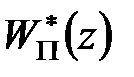 включає множник
включає множник 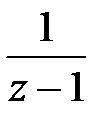 . Оскільки
. Оскільки 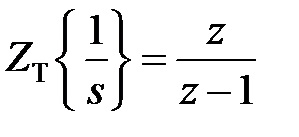 передаточна функція
передаточна функція 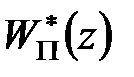 міститиме вказаний множник, якщо безперервна частина (тобто
міститиме вказаний множник, якщо безперервна частина (тобто 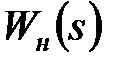 ) включає інтегруючу ланку. Тут важливо, щоб безперервна частина, а не приведена безперервна частина, включала інтегруючу ланку. Це пов'язано з тим, що множник
) включає інтегруючу ланку. Тут важливо, щоб безперервна частина, а не приведена безперервна частина, включала інтегруючу ланку. Це пов'язано з тим, що множник 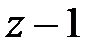 у знаменнику
у знаменнику 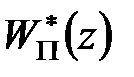 який з'являється із-за інтегруючої ланки у формувачі, скорочується з аналогічним множником, що з'являється в чисельнику.
який з'являється із-за інтегруючої ланки у формувачі, скорочується з аналогічним множником, що з'являється в чисельнику.
Наприклад, при фіксаторі нульового порядку передаточна функція формувача має вигляд 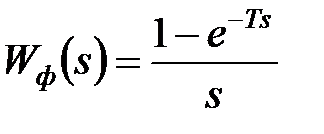 і
і
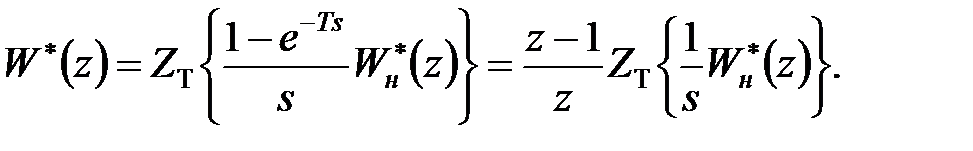
|
Як бачимо, в цьому випадку з'являється множник 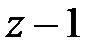 у чисельнику, який скорочується з таким же множником в знаменнику, що з'являється через множник
у чисельнику, який скорочується з таким же множником в знаменнику, що з'являється через множник  у передаточній функції приведеної безперервної частини.
у передаточній функції приведеної безперервної частини.
Як побачимо далі на прикладі, те ж саме відбувається, коли передаточна функція формуючої ланки має вигляд 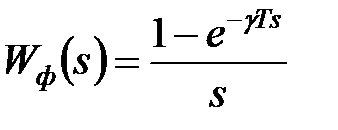 .
.
Отже, дискретна система буде астатичною, якщо передаточна функція дискретного фільтру (регулятора) включає множник 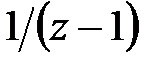 або безперервна частина містить інтегруючу ланку. Порядок астатизму системи дорівнює сумі числа інтегруючих ланок в безперервній частині і показнику ступеня
або безперервна частина містить інтегруючу ланку. Порядок астатизму системи дорівнює сумі числа інтегруючих ланок в безперервній частині і показнику ступеня 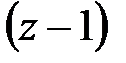 у знаменнику дискретного фільтру.
у знаменнику дискретного фільтру.
Приклад 26.1. Припустимо, що (див. рис. 26.1)
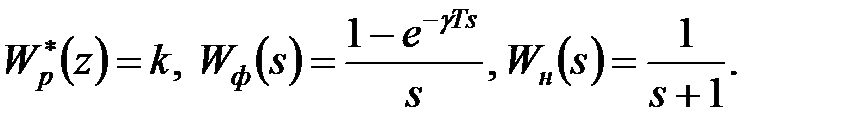
Показати, що дана система є статичною.
Рішення. Знайдемо передаточну функцію розімкненої дискретної системи. Припустимо, що 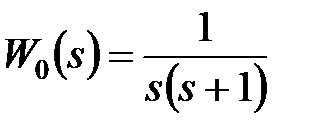 . Передаточна функція розімкненої дискретної системи
. Передаточна функція розімкненої дискретної системи
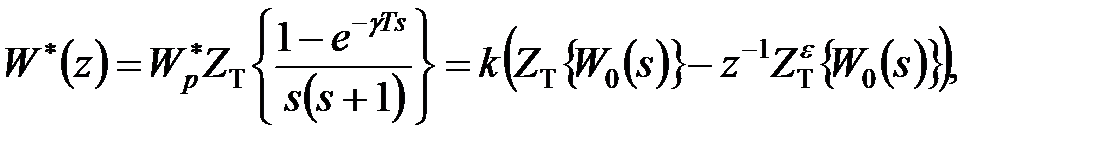
|
де 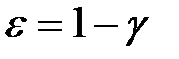 і
і

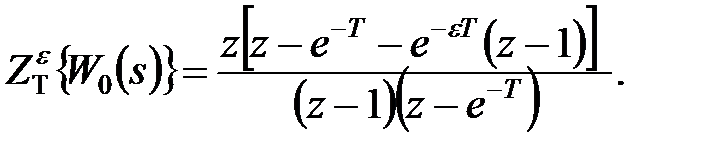
Підставивши ці вирази, для передаточної функції розімкненої системи отримаємо 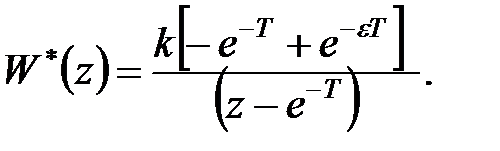
Передаточна функція розімкненої системи не містить в знаменнику множник 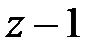 . Отже, дана система є статичною.
. Отже, дана система є статичною.
Приклад 26.2. Припустимо, що в дискретній системі (див. рис. 26.1)

Задаюча дія 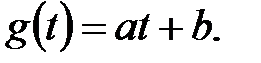 Визначити сталу помилку.
Визначити сталу помилку.
Рішення. В даному випадку стала помилка визначається за формулою
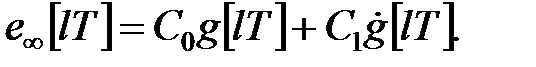
|
Передаточна функція регулятора містить в знаменнику множник  у першому ступені, і безперервна частина містить одну інтегруючу ланку. Тому система має астатизм другого порядку і
у першому ступені, і безперервна частина містить одну інтегруючу ланку. Тому система має астатизм другого порядку і 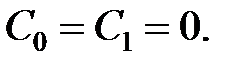 Отже
Отже 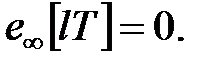
Дата добавления: 2017-08-01; просмотров: 214;
