Синтез систем з фіксованою структурою
Завдання синтезу систем з фіксованою структурою ставиться таким чином: заданий об'єкт і вибрана структура регулятора; потрібно визначити параметри регулятора, що забезпечують задані вимоги до якості системи, що синтезується.
Структура регулятора (системи) визначається в основному з вимог до структурної стійкості і якості системи, що синтезується, в сталому режимі. Параметри регулятора визначаються виходячи з вимог до якості системи в перехідному режимі. На параметри можуть бути накладені обмеження, витікаючі з вимог допустимої помилки в сталому режимі або яких-небудь інших вимог.
Розглянемо постановку і рішення задачі синтезу параметрів на конкретних прикладах.
Приклад 27.1. Дискретний елемент є фіксатор нульового порядку, період квантування 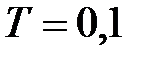 і передаточна функція безперервної частини має вигляд
і передаточна функція безперервної частини має вигляд 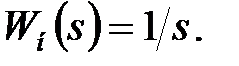 Визначити тип і параметри регулятора виходячи з таких вимог до системи:
Визначити тип і параметри регулятора виходячи з таких вимог до системи: 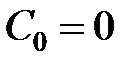 ,
, 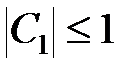 ,
, 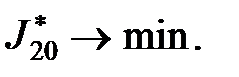
Рішення. Оскільки коефіцієнт позиційної помилки дорівнює нулю, а коефіцієнт швидкісної помилки не дорівнює нулю, система повинна бути астатичною і мати астатизм першого порядку. Але у зв'язку з тим, що безперервна частина включає інтегратор, можна вибрати П-регулятор 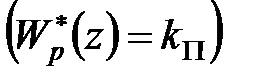 .
.
При фіксаторі нульового порядку передаточна функція формуючої ланки має вигляд 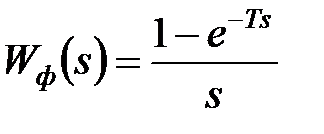 . Тому передаточна функція приведеної безперервної частини (ПБЧ) має вигляд
. Тому передаточна функція приведеної безперервної частини (ПБЧ) має вигляд
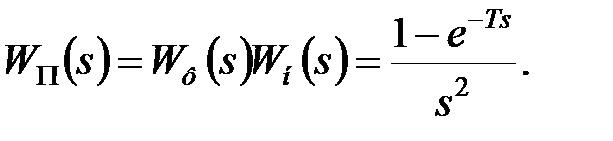
|
Передаточна функція розімкненої дискретної моделі дорівнює
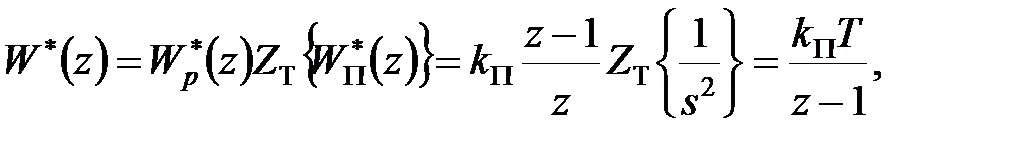
|
і передаточна функція помилки (замкнутої системи) –
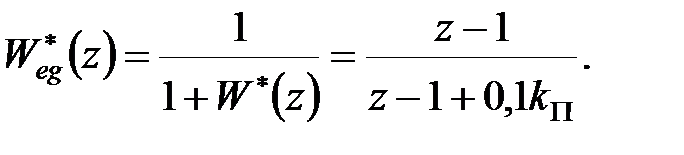
|
Оскільки 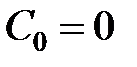 коефіцієнт швидкісної помилки можна визначити за формулою
коефіцієнт швидкісної помилки можна визначити за формулою
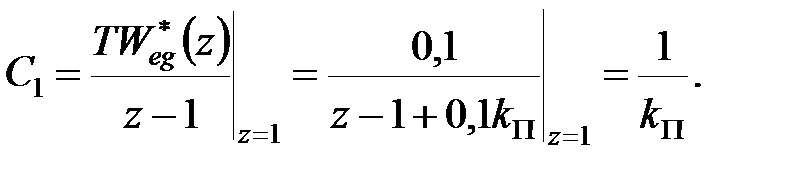
|
Умова 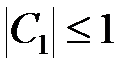 буде виконана, якщо
буде виконана, якщо 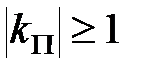 . Характеристичне рівняння має вигляд
. Характеристичне рівняння має вигляд
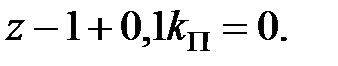
|
Його корінь 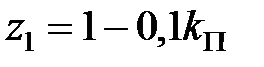 по модулю буде менше одиниці, якщо
по модулю буде менше одиниці, якщо 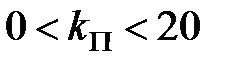 . Таким чином, система буде стійка і будуть виконані вимоги до якості в сталому режимі, якщо
. Таким чином, система буде стійка і будуть виконані вимоги до якості в сталому режимі, якщо 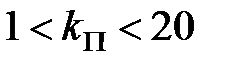 .
.
Знайдемо вираз для помилки при 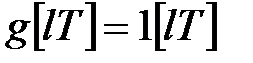 :
:
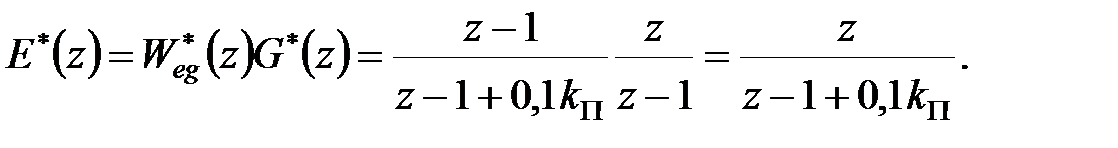
|
Оскільки система астатична, стала помилка є 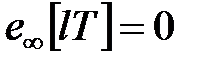 і перехідна складова помилки
і перехідна складова помилки 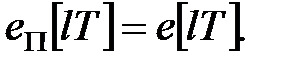 Тому
Тому 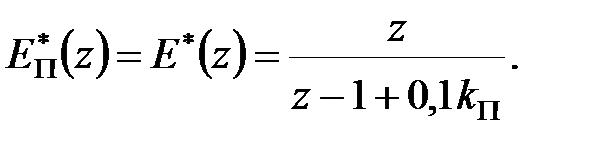
По формулі розкладання маємо
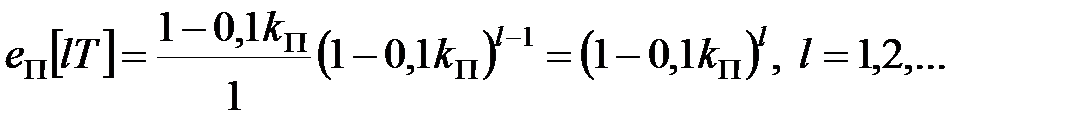
|
Як легко перевірити, ця формула справедлива і при 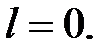 Сумарна квадратична помилка має вигляд
Сумарна квадратична помилка має вигляд
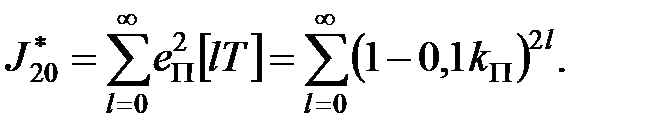
|
По формулі суми нескінченно убуваючої прогресії маємо

|
Звідси витікає, що 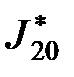 досягає мінімуму при отриманих вище обмеженнях на
досягає мінімуму при отриманих вище обмеженнях на 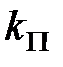 коли
коли 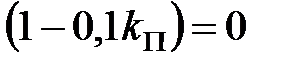 або
або 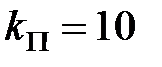 . Таким чином, рішенням даної задачі є
. Таким чином, рішенням даної задачі є 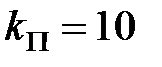 .
.
Приклад 27.2. Дискретний елемент представляє фіксатор нульового порядку, період квантування рівний 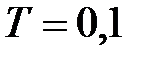 і передаточна функція безперервної частини є
і передаточна функція безперервної частини є 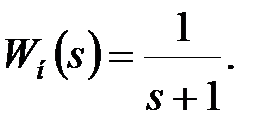
Визначити тип і параметри регулятора, при якому статична помилка дорівнює нулю і перехідний процес закінчується за кінцеве число кроків.
Рішення. Щоб статична помилка дорівнювала нулю, виберемо пропорційно-сумарний закон управління: 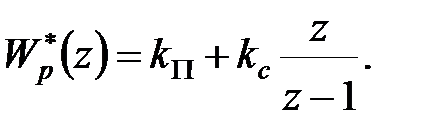
Передаточна функція формуючої ланки має вигляд
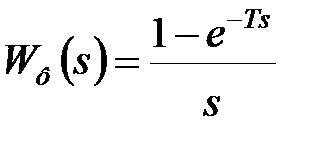 ,
,
передаточна функція приведеної безперервної частини –
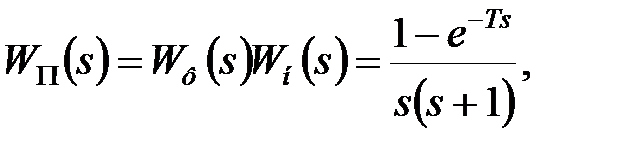
і передаточна функція розімкненої дискретної моделі –
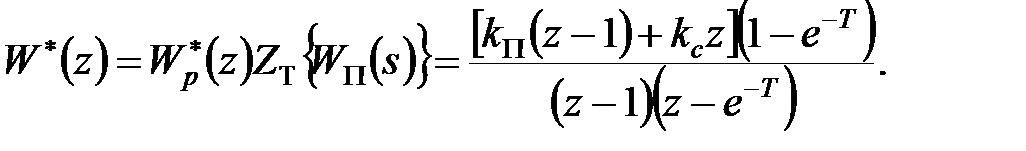
Прийнявши 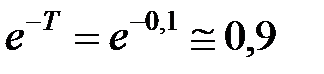 отримаємо
отримаємо
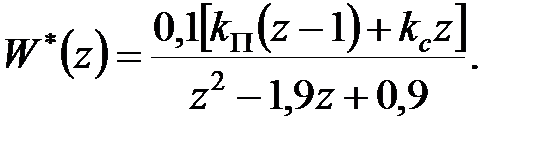
Передаточна функція замкнутої системи (див. рис. 27.1) має вигляд

де
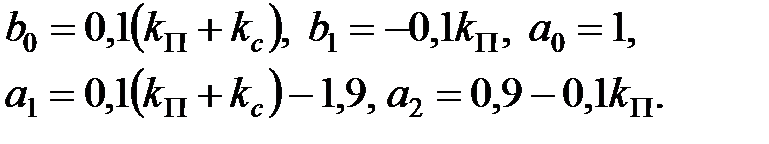
Умова закінчення перехідного процесу за кінцеве число кроків приймає вигляд
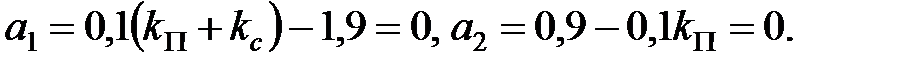
Звідси 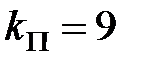 і
і 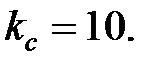
Дата добавления: 2017-08-01; просмотров: 212;
