Спосіб прямого програмування

Розглянемо перехід від опису імпульсної системи за допомогою Z-передаточних функцій до опису за допомогою змінних стану. Як вже наголошувалося, вибір змінних стану не є єдиним, і визначається вибором відповідного базису. Практично зручним прийомом вибору змінних стану є складання схем моделювання дискретних систем. Схеми включають елементи затримки на такт і суматори. При виборі змінних стану імпульсних систем за них зручно приймати виходи елементів затримки на такт.

Розглянемо три способи переходу від Z-передаточної функції дискретної системи до рівнянь у просторі станів: способи прямого програмування, послідовного програмування і паралельного програмування на прикладі ланки другого порядку з одним входом і одним виходом і передаточною функцією

.

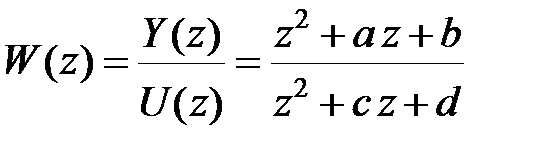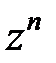При способі прямого програмування, розділивши чисельник і знаменник передаточної функції на (у загальному випадку на ), отримаємо

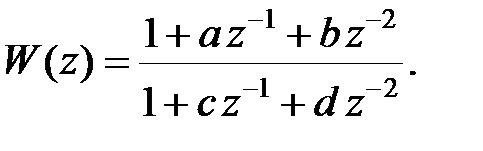
(31.1)

За визначенням передаточної функції

.

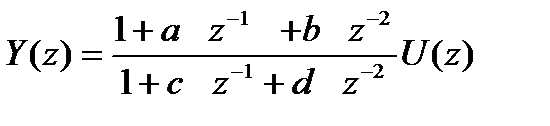Введемо нову змінну e[kT], Z -перетворення якої має вигляд

.

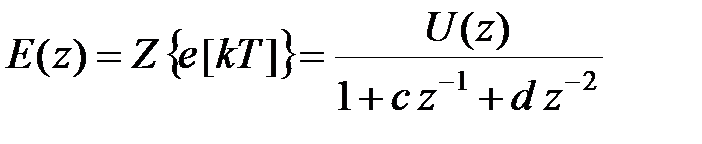Тоді

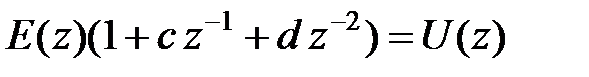
або

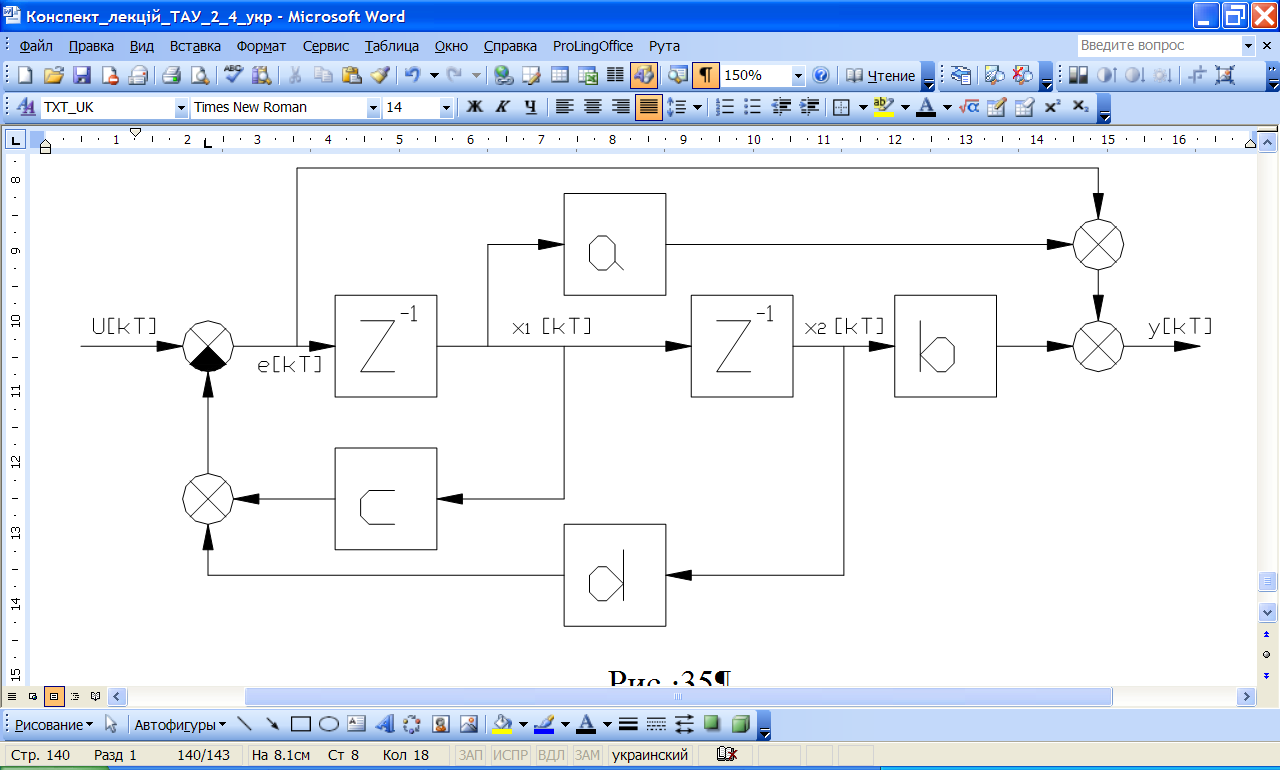
Відповідно до виразу (31.1) складаємо схему моделювання (рис.31.1). При цьому враховуємо, що множник 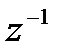відповідає затримці змінної на один такт квантування.

Рис. 30.1. Схема моделювання (метод прямого програмування)

Рівняння стану системи можна отримати, записуючи співвідношення, що зв'язують координати на виходах елементів затримки. У результаті маємо

, .

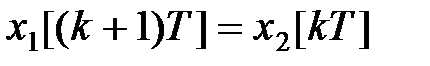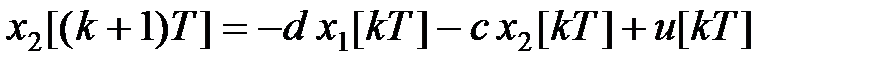(31.2)

Оскільки

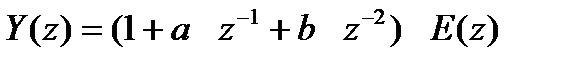
і при цьому

,

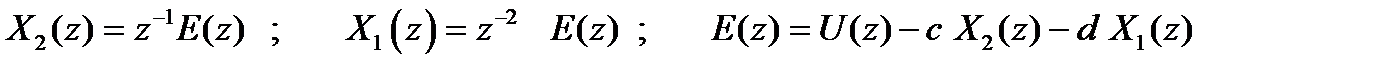то для вихідний змінної у[kT] отримаємо рівняння

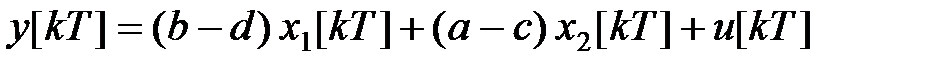
(31.3)

Таким чином, рівняння у просторі станів приймають вигляд (31.2). (31.3), а матриці Ф, Н, C, D визначаються виразами

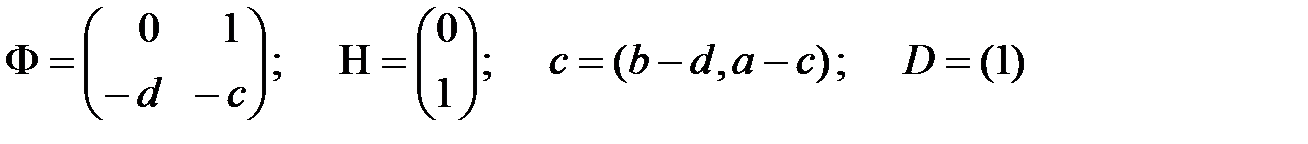
Запис системи рівнянь для загального випадку не представляє складності. При цьому матриця Ф матиме структуру, аналогічну власній матриці системи диференціальних рівнянь, записаних в першій нормальній формі Коші.