ЛЕКЦІЯ 30 Оптимізація одноконтурних АСР з багатопараметричними регуляторами
У промислових автоматичних системах регулювання, як правило, рекомендується застосовувати типовий ПІД-регулятор і його окремий випадок ПІ-регулятор, в якому з ПІД-алгоритма виключена складова, пропорційна першій похідній від відхилення регульованого параметра.
Відомо, що ПІД-алгоритм вважається достатньо близьким до оптимального, заснованого на теорії прогнозу Колмагорова-Винера. Проте, може опинитися, що динамічна точність регулювання з ПІД-регулятором стає недостатньою. У таких випадках зазвичай йдуть на ускладнення інформаційної структури, прикладом чого можуть служити каскадні системи автоматичного регулювання, а також системи з додатковим імпульсом по похідній з проміжної точки.
Враховуючи сучасні тенденції формування регулюючих пристроїв в мікропроцесорних контроллерах, представляється можливим йти шляхом вдосконалення і ускладнення алгоритмів функціонування автоматичних регуляторів. Такому напряму розвитку сприяє активне впровадження в теорію і практику автоматичного управління технологій штучного інтелекту. В першу чергу це відноситься до штучних нейромереж (ІНМ) для структурної реалізації алгоритмів управління і нових чисельних методів оптимізації на основі генетичних алгоритмів (ГА) [10-14].
З урахуванням викладеного, одним із способів підвищення динамічної точності в одноконтурній АСР може бути введення в алгоритм регулюючого пристрою складових, пропорційних похідним від відхилення регульованого параметра другого, а при необхідності і вищого порядку.
Оптимальний синтез АСР прийнято проводити по динамічних характеристиках об'єкту регулювання, представлених, як правило, у вигляді передаточних функцій 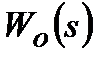 отриманих шляхом адекватної апроксимації експериментальних кривих розгону. При цьому, структуру
отриманих шляхом адекватної апроксимації експериментальних кривих розгону. При цьому, структуру 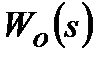 представляють у вигляді раціонального дробу функції
представляють у вигляді раціонального дробу функції 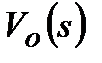 і ланки запізнювання на якийсь час
і ланки запізнювання на якийсь час 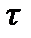 :
:
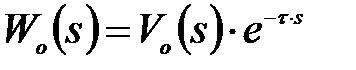 . .
| (30.1) |
Дробно-раціональна частина для найбільш поширених в промисловості об'єктів з самовирівнюванням представляється у вигляді ланцюга з " 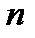 " послідовно включених аперіодичних ланок з постійними часу
" послідовно включених аперіодичних ланок з постійними часу 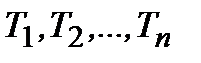 :
:
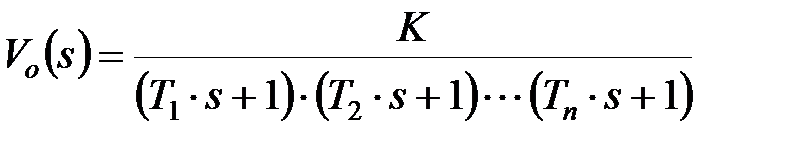 . .
| (30.2) |
З урахуванням системного підходу до рішення задачі оптимального синтезу АСР порядок знаменника у виразі (30.2) визначається, з одного боку, з умови адекватності апроксимуючої передаточної функції, з іншого боку, отримана таким чином структура визначатиме алгоритм оптимального регулятора, передаточна функція якого в першому наближенні має вигляд [10]:
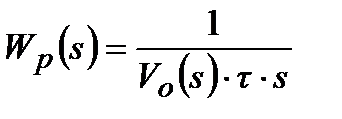 . .
| (30.3) |
З урахуванням (30.1, 30.2) після перетворень вираз (30.3) прийме вигляд:
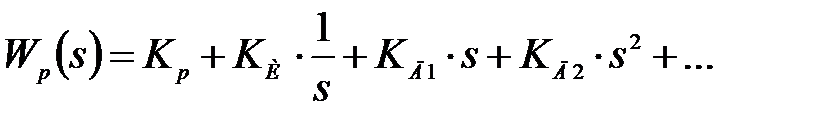 , ,
| (30.4) |
де 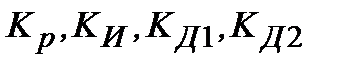 - настроювальні параметри регулятора.
- настроювальні параметри регулятора.
З урахуванням прийнятих в технічній літературі позначень настроювальних параметрів, вираз (30.4) можна записати:
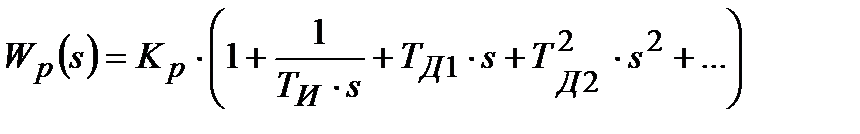 , ,
| (30.5) |
де 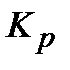 - коефіцієнт передачі;
- коефіцієнт передачі; 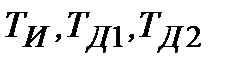 - постійні інтегрування і диференціювання.
- постійні інтегрування і диференціювання.
Неважко відмітити, що для функції 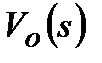 при
при 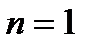 оптимальним буде ПІ-алгоритм, при
оптимальним буде ПІ-алгоритм, при 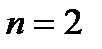 ПІД-алгоритм, при
ПІД-алгоритм, при 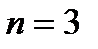 ПІДД2-алгорітм і так далі. При цьому, чисельні значення настроювальних параметрів досить легко можуть бути виражені через параметри передаточної функції об'єкту (табл.30.1).
ПІДД2-алгорітм і так далі. При цьому, чисельні значення настроювальних параметрів досить легко можуть бути виражені через параметри передаточної функції об'єкту (табл.30.1).
Таким чином, в ПІДД2-алгоритмі додається складова, пропорційна другій похідній або прискоренню відхилення регульованого параметра з постійною часу 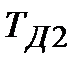 . Аналогічно можна говорити і про третю похідну, що характеризує швидкість прискорення.
. Аналогічно можна говорити і про третю похідну, що характеризує швидкість прискорення.
Проте, отримані таким чином регулятори навряд чи відразу і беззастережно можуть бути прийняті до практичного застосування, проте знання алгоритмів їх функціонування дозволить оцінити граничні можливості управління об'єктом і сформулювати відповідні рекомендації.
При пошуці оптимальних настроювальних параметрів чисельними методами зручніше оперувати з параметрами 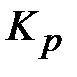 ,
, 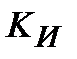 .
.
У сучасних процесорних контроллерах формування функціонального блоку (ФБ), що визначає алгоритм функціонування регулюючого пристрою, здійснюється відповідно до призначення регулятора і типу вживаного виконавчого механізму.
Розрізняють імпульсні регулятори, що працюють з широтноімпульсним модулятором (ШІМ) і електричним виконавчим механізмом (ЕВМ), і аналогові регулятори, вживані як допоміжні в каскадних АСР, а також в одноконтурних АСР з пропорційними виконавчими механізмами (ПВМ). До останніх належать мембранні пневматичні виконавчі механізми, широко використовувані в хімічних і нафтохімічних виробництвах.
Таблиця 30.1
| Параметри налаштувань | 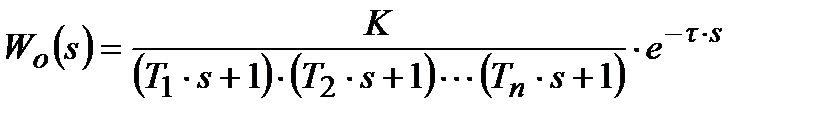
| ||
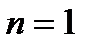 ПІ-алгоритм ПІ-алгоритм
| 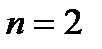 ПІД-алгоритм ПІД-алгоритм
| 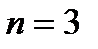 ПІДД2-алгоритм ПІДД2-алгоритм
| |
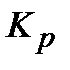
| 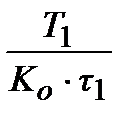
| 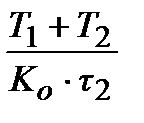
| 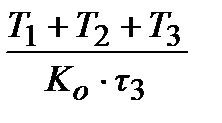
|
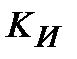
| 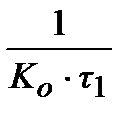
| 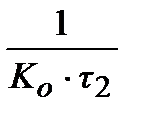
| 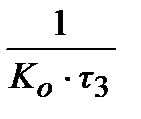
|
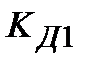
| – | 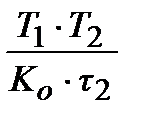
| 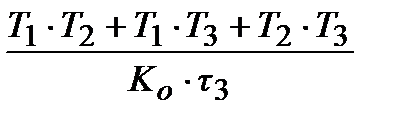
|
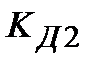
| – | – | 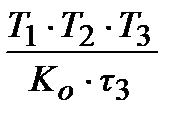
|
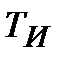
| 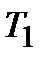
| 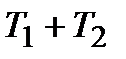
| 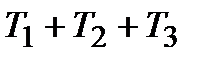
|
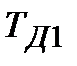
| – | 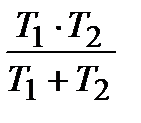
| 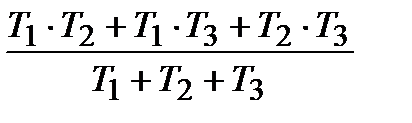
|
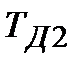
| – | – | 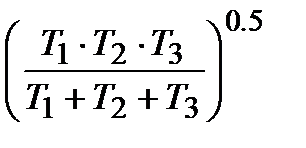
|
Спрощені структурні схеми регуляторів показані на рис. 30.1.
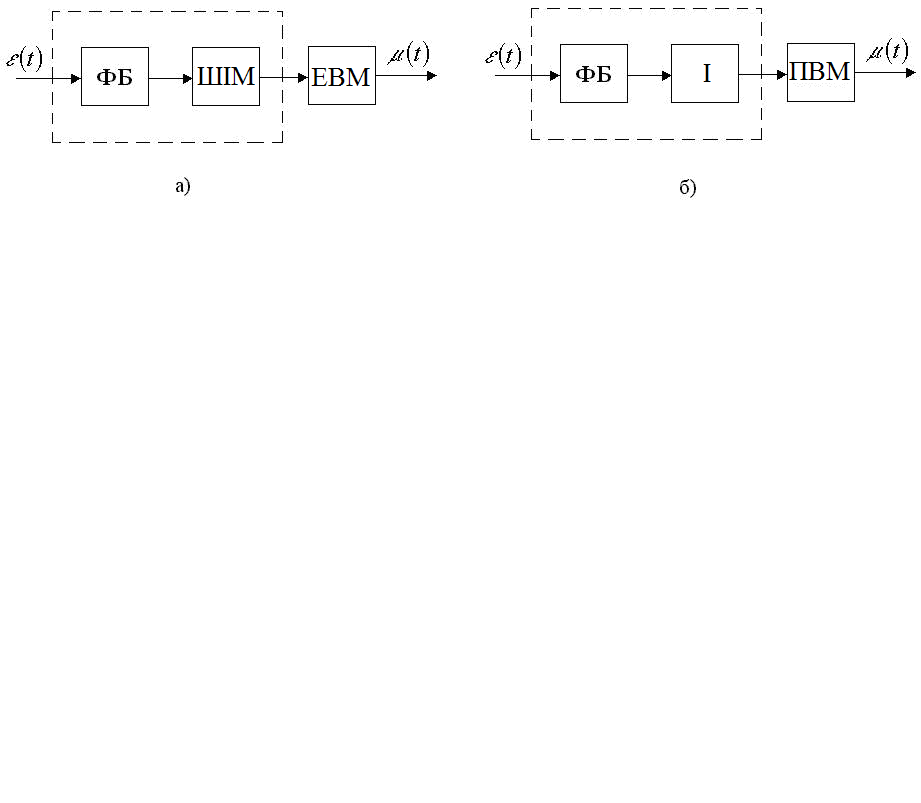
Рис. 30.1. Структури реалізації регуляторів
а) імпульсний регулятор з електричним виконавчим механізмом;
б) аналоговий регулятор з пропорційним виконавчим механізмом (І-інтегратор).
Функціональний блок (ФБ) для ПИДД2-регулятора у обох структурах може бути реалізований однаково у вигляді ПДД2Д3-ланки с передаточной функцієй:
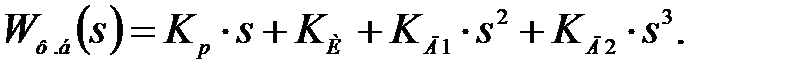
| (30.6) |
У першому наближенні ШІМ і ЕВМ (рис. 30.1 а) представляється можливим описати передаточною функцією інтегруючої ланки. Інтегруючою ланкою без яких-небудь допущень є і інтегратор (рис. 30.1 б). З урахуванням сказаного, передаточна функція для регуляторів аналізованих структур запишеться у вигляді:
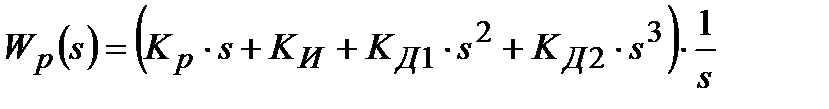 . .
| (30.7) |
Реалізація ФБ в контроллері виконується шляхом розрахунку відхилення регульованого параметра від завдання і його похідних з коефіцієнтами пропорційності, що є настроювальними параметрами. Тому, першим очевидним кроком на шляху вдосконалення структури і алгоритму регулятора в порівнянні з ПІД-алгоритмом буде введення у ФБ додаткової складової, пропорційної третії похіднії від відхилення регульованого параметра.
Введення додаткових складових в алгоритм регулятора приводить до збільшення числа настроювальних параметрів, що робить відомі аналітичні методи розрахунку із-за їх складності практично непридатними. У зв'язку з цим виникає необхідність застосування алгоритмів чисельної оптимізації з використанням прийомів імітаційного моделювання. При такому підході як цільовий критерій для ступінчастих збурень, що вносяться роздільно по каналу регулюючої дії 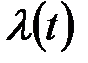 і по каналу завдання
і по каналу завдання 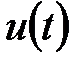 пропонується використовувати інтегральну оцінку модуля перехідного процесу:
пропонується використовувати інтегральну оцінку модуля перехідного процесу:
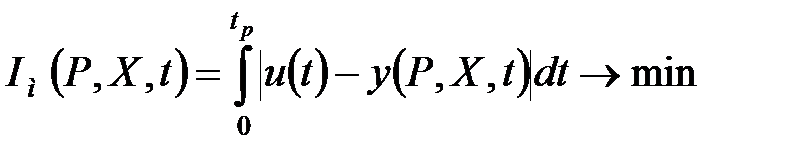 , ,
| (30.8) |
де 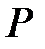 - вектор настроювальних параметрів
- вектор настроювальних параметрів 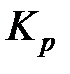 ,
, 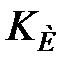 ,
, 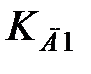 ,
, 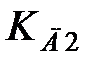 ;
; 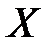 - вектор вхідних впливів
- вектор вхідних впливів 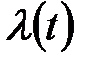 ,
, 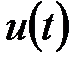 ;
; 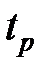 - час перехідного процесу.
- час перехідного процесу.
Мінімальне значення інтеграла (30.8) не є інваріантним щодо даних вхідних впливів, тому настройки пропонується визначати залежно від призначення АСР (для стабілізуючої системи при 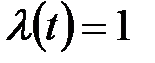
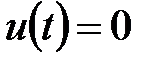 ). Метод дозволяє визначати і компромісні настройки, що забезпечують мінімальне значення суми інтегральних оцінок при роздільній подачі збурень
). Метод дозволяє визначати і компромісні настройки, що забезпечують мінімальне значення суми інтегральних оцінок при роздільній подачі збурень 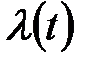 і
і 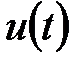 . З урахуванням викладеного, вектор
. З урахуванням викладеного, вектор 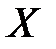 може бути представлений у вигляді матриці
може бути представлений у вигляді матриці
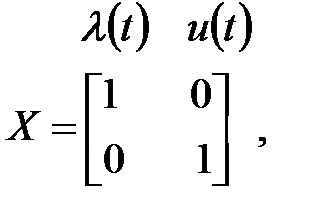
| (30.9) |
де перший рядок визначає оптимальну настройку стабілізуючої АСР, при якій мінімізується інтеграл:
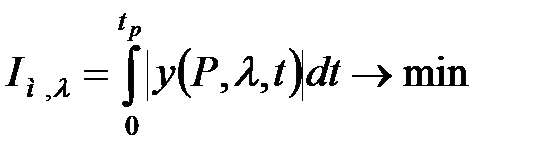 , ,
| (30.10) |
а другий рядок визначає оптимальні настроювальні параметри стежачої АСР, що мінімізують інтеграл вигляду:
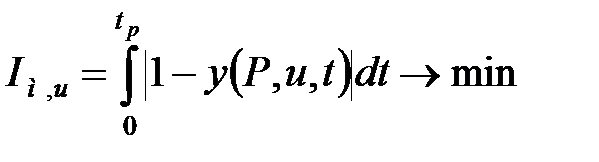 . .
| (30.11) |
Компромісна настройка мінімізує суму інтегралів:
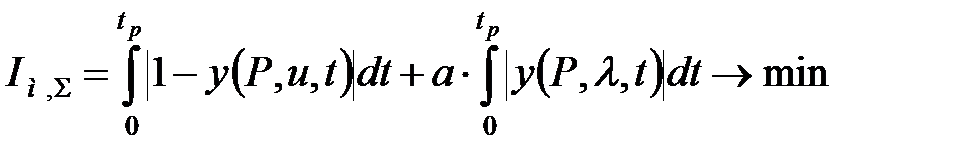 , ,
| (30.12) |
де 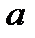 - масштабний коефіцієнт, що робить інтеграли зіставними.
- масштабний коефіцієнт, що робить інтеграли зіставними.
У приведених нижче ілюстраційних прикладах для оптимізації настроювальних параметрів ПІД- и ПІДД2-регуляторів використовувалася авторська версія модифікованого генетичного алгоритму [12].
Численні розрахунки, проведені за пропонованою методикою, показали, що критерії, що рекомендуються, мають чітко виражений екстремум, що забезпечує для АСР з розглянутими алгоритмами регулювання достатньо високий запас стійкості. Для забезпечення бажаного характеру перехідного процесу, в першу чергу, обумовленого вимогами робастности, представляється можливість ввести обмеження, як на окремі настроювальні параметри і їх співвідношення, так і на показники, що безпосередньо характеризують запас стійкості.
Слід відмітити, що оцінка запасу стійкості по ступеню загасання 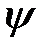 і її зв'язок з кореневим показником коливальності
і її зв'язок з кореневим показником коливальності 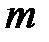 припускає типовий вид перехідного процесу в АСР і практично обмежується системами з ПІ-регулятором. Перехідні процеси з регуляторами, що містять похідні, помітно відрізняються від типових і оцінка їх запасу стійкості по ступеню загасання стає складною. У зв'язку з цим, пропонується використовувати інтегральний ступінь загасання
припускає типовий вид перехідного процесу в АСР і практично обмежується системами з ПІ-регулятором. Перехідні процеси з регуляторами, що містять похідні, помітно відрізняються від типових і оцінка їх запасу стійкості по ступеню загасання стає складною. У зв'язку з цим, пропонується використовувати інтегральний ступінь загасання 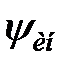 визначувану відношенням лінійного інтеграла
визначувану відношенням лінійного інтеграла 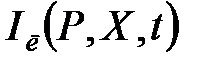 до інтеграла по модулю
до інтеграла по модулю 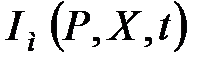 .
.
Представляють інтерес обмеження на коефіцієнт передачі регулятора 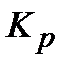 , що в значній мірі визначає чутливість системи, а також що рекомендується у ряді публікацій [2,7] як настроювальний параметр для ПІД-регулятора коефіцієнт
, що в значній мірі визначає чутливість системи, а також що рекомендується у ряді публікацій [2,7] як настроювальний параметр для ПІД-регулятора коефіцієнт 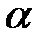 визначуваний відношенням постійної диференціювання до постійної часу інтегрування, по аналогії з якою можна ввести подібні коефіцієнти
визначуваний відношенням постійної диференціювання до постійної часу інтегрування, по аналогії з якою можна ввести подібні коефіцієнти 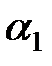 і
і 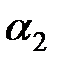 для ПІДД2-регулятора:
для ПІДД2-регулятора:
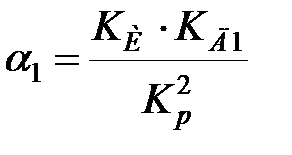 ; ; 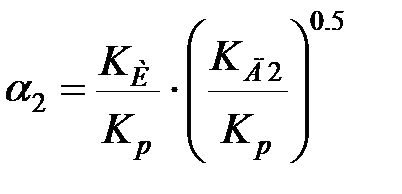 . .
| (30.13) |
Поняття, що зустрічається в технічній літературі 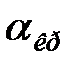 для ПІД-регулятора є не зовсім коректним, оскільки очевидним є оптимальне значення
для ПІД-регулятора є не зовсім коректним, оскільки очевидним є оптимальне значення 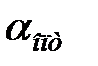 відповідне оптимальним настройкам, що мінімізують прийнятий цільовий критерій. Будь-які інші значення
відповідне оптимальним настройкам, що мінімізують прийнятий цільовий критерій. Будь-які інші значення 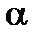 є лише обмеженнями, що наприкінець призводять до зниження якості регулювання.
є лише обмеженнями, що наприкінець призводять до зниження якості регулювання.
Розглянуті вище обмеження вводяться в цільовий критерій у вигляді функцій штрафу:
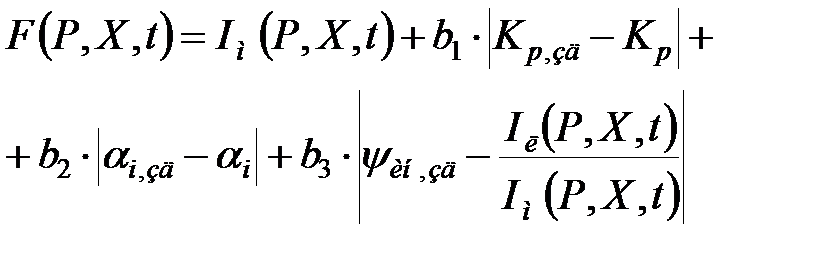 , ,
| (30.14) |
де 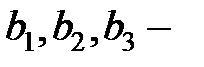 вагові коефіцієнти;
вагові коефіцієнти; 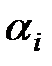 - відношення постійної диференціювання
- відношення постійної диференціювання 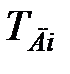 до постійної інтегрування
до постійної інтегрування 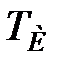 .
.
Перераховані обмеження можуть бути використані для підбору робастних настройок, що забезпечують практичну працездатність АСР.
Як приклад, що ілюструє викладене, наводяться результати розрахунку АСР температури перегрітої пари [1]. Математична модель об'єкту регулювання представлена у вигляді передаточної функції котла ТЕС по каналу: переміщення регулюючого органу витрати води, що охолоджує, в пароохолоджувач – температура перегріву пари. Передаточна функція 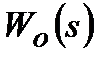 отримана шляхом апроксимації експериментальної перехідної характеристики:
отримана шляхом апроксимації експериментальної перехідної характеристики:
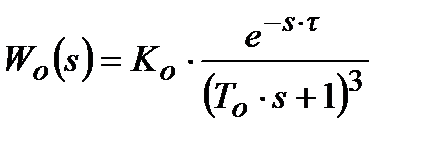 , ,
| (30.15) |
де 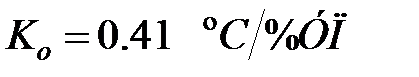 ;
; 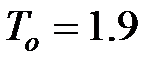 хв;
хв; 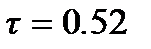 хв.
хв.
Результати настройки ПІД- і ПІДД2-регуляторів для цільових функцій вигляду (30.10, 30.11, 30.12) без обмежень, отримані методом імітаційного моделювання з використанням модифікованого генетичного алгоритму, приведені в табл.30.2.
Параметрична оптимізація стабілізуючої АСР проводилася шляхом пошуку мінімального значення 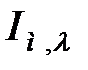 для одиничної ступінчастої дії по каналу регулюючого органу
для одиничної ступінчастої дії по каналу регулюючого органу 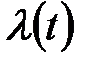 (точки 1,2) для стежачої АСР мінімізувався інтеграл
(точки 1,2) для стежачої АСР мінімізувався інтеграл 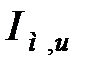 для одиничної ступінчастої дії
для одиничної ступінчастої дії 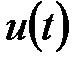 (точки 3,4) і інтеграл
(точки 3,4) і інтеграл 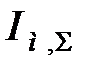 для компромісної настройки (точки 5,6).
для компромісної настройки (точки 5,6).
Там же приведені настроювальні параметри ПІД-регулятора по даним [1] (точка 7) і наближені значення настроювальних параметрів ПІДД2-регулятора, обчислені по формулах, наведених в табл.1 (точка 8).
Таблиця 30.2.
| Параметри | 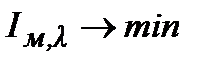
| 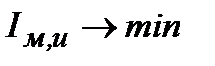
| 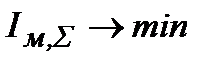
| 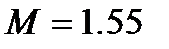
| З табл.30.1 | |||
| ПІД | ПІДД2 | ПІД | ПІДД2 | ПІД | ПІДД2 | ПІД | ПІДД2 | |
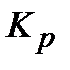
| 12.35 | 81.33 | 5.58 | 12.64 | 6.57 | 15.81 | 7.59 | 24.36 |
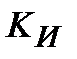
| 6.26 | 25.07 | 1.04 | 2.12 | 1.82 | 2.88 | 3.18 | 4.28 |
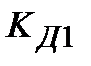
| 28.92 | 61.05 | 12.18 | 24.63 | 14.01 | 27.89 | 14.24 | 46.29 |
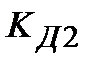
| - | 41.02 | - | 18.47 | - | 20.54 | - | 29.31 |
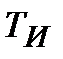
| 1.973 | 3.244 | 5.349 | 5.977 | 3.614 | 5.493 | 2.387 | 5.692 |
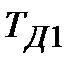
| 2.341 | 0.751 | 2.183 | 1.949 | 2.133 | 1.765 | 1.875 | 1.901 |
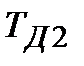
| - | 0.710 | - | 1.461 | - | 1.299 | - | 1.090 |
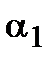
| 1.186 | 0.231 | 0.408 | 0.326 | 0.590 | 0.321 | 0.785 | 0.33 |
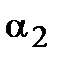
| - | 0.219 | - | 0.244 | - | 0.236 | - | 0.191 |
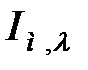
| 0.305 | 0.045 | 0.991 | 0.473 | 0.683 | 0.347 | 0.581 | 0.234 |
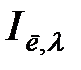
| 0.159 | 0.040 | 0.962 | 0.473 | 0.549 | 0.347 | 0.314 | 0.234 |
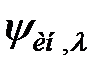
| 0.520 | 0.880 | 0.970 | 1.00 | 0.80 | 1.00 | 0.54 | 1.00 |
Перехідні процеси в одноконтурній АСР з ПІД- і ПІДД2-регуляторами, оптимально налаштованими на ступінчасте збурення 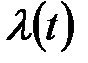 (стабілізуюча АСР, т. 1,2 табл. 30.2) показані на рис. 30.2 а, а перехідні процеси на ступінчасту дію за завданням
(стабілізуюча АСР, т. 1,2 табл. 30.2) показані на рис. 30.2 а, а перехідні процеси на ступінчасту дію за завданням 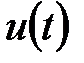 (стежача АСР, т.3,4 табл.30.2) на рис. 30.2.б. Там же для порывняння наведені перехідні процеси для АСР с ПІД-регулятором, настроєним по даним [1] (т.7 табл.30.2) і для АСР с ПІДД2-регулятором, настроєним по формулах табл.30.1 (т.8 табл. 30.2).
(стежача АСР, т.3,4 табл.30.2) на рис. 30.2.б. Там же для порывняння наведені перехідні процеси для АСР с ПІД-регулятором, настроєним по даним [1] (т.7 табл.30.2) і для АСР с ПІДД2-регулятором, настроєним по формулах табл.30.1 (т.8 табл. 30.2).
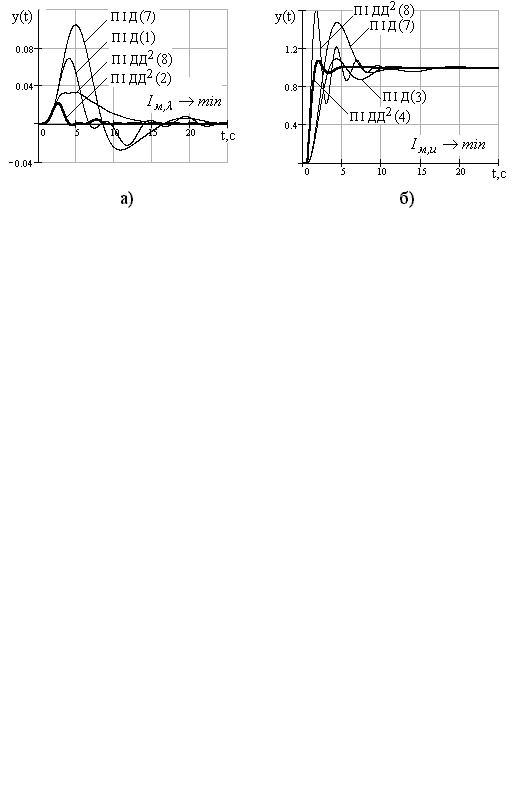
Рис.30.2. Перехідні процеси в АСР з ПІД- і ПІДД2-регуляторами
а) стабілізуюча АСР, налаштована на 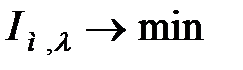 ;
;
б) стежача АСР, настроєна на 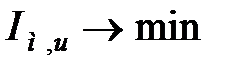 .
.
На рис.30.3 представлені перехідні процеси в АСР з ПІД- і ПІДД2-регуляторами при компромісних настройках по критерію 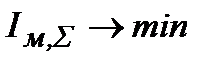 (т. 5,6 табл.30.2). Там же для порівняння показані процеси для ПІД-регулятора, настроєного по даним [1] (т. 7 табл.30.2).
(т. 5,6 табл.30.2). Там же для порівняння показані процеси для ПІД-регулятора, настроєного по даним [1] (т. 7 табл.30.2).
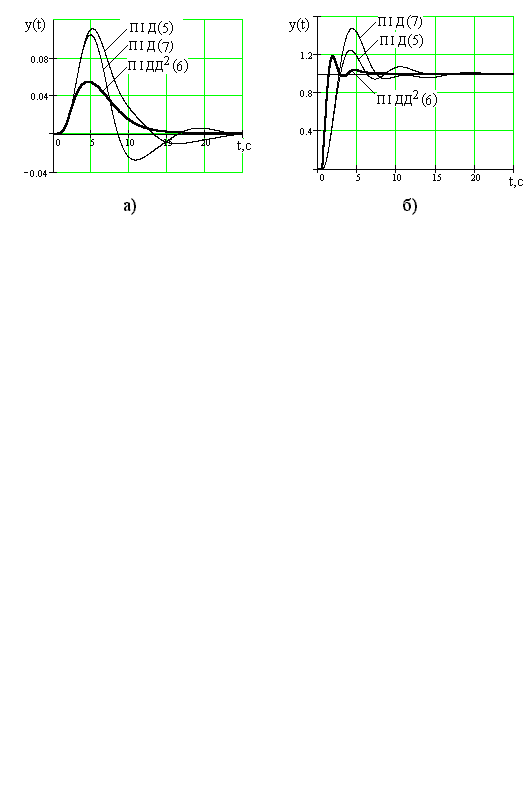
Рис.30.3. Перехідні процеси в АСР з ПІД- ПІДД2-регуляторами, налаштованими на компромісний критерій 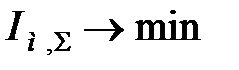
а) збурення 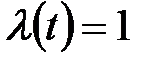 по каналу регулюючого органу;
по каналу регулюючого органу;
б) збурення 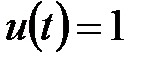 по керуючому впливу.
по керуючому впливу.
Настроювальні параметри і основні показники АСР з ПІД- і ПІДД2-регуляторами, отримані при введенні обмежень, представлені в табл.30.3.
Таблиця 30.3.
| Параметри | ПІД | ПІДД2 | |||||
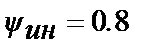
| 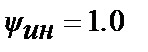
| 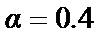
| 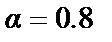
| 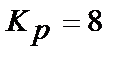
| 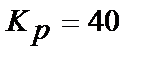
| ||
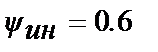
| 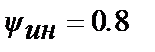
| 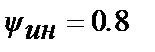
| |||||
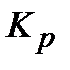
| 11.24 | 11.84 | 12.98 | 12.62 | 8.00 | 8.00 | |
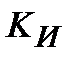
| 3.503 | 1.723 | 3.342 | 5.072 | 3.305 | 2.364 | 15.87 |
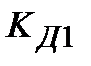
| 19.57 | 19.36 | 20.17 | 25.13 | 18.22 | 11.57 | 48.84 |
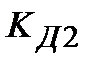
| - | - | - | - | - | - | 23.21 |
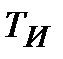
| 3.209 | 6.872 | 3.884 | 2.488 | 2.418 | 3.384 | 2.520 |
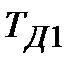
| 1.741 | 1.635 | 1.539 | 1.991 | 2.277 | 1.446 | 1.221 |
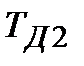
| - | - | - | - | - | - | 0.761 |
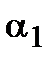
| 0.543 | 0.238 | 0.400 | 0.800 | 0.942 | 0.427 | 0.484 |
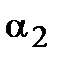
| - | - | - | - | - | - | 0.302 |
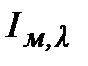
| 0.358 | 0.579 | 0.385 | 0.315 | 0.505 | 0.529 | 0.079 |
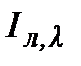
| 0.286 | 0.579 | 0.300 | 0.197 | 0.303 | 0.423 | 0.063 |
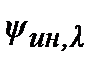
| 0.800 | 1.000 | 0.779 | 0.626 | 0.600 | 0.800 | 0.800 |
Оптимізація АСР з ПІД-регулятором проводилася по 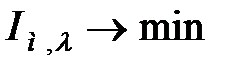 з обмеженням на інтегральний ступінь загасання
з обмеженням на інтегральний ступінь загасання 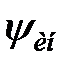 (т. 1,2 табл. 30.3) і на показник
(т. 1,2 табл. 30.3) і на показник 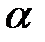 (т. 3,4 табл.30.3). Там же приведені результати розрахунку при сумісних обмеженнях на коефіцієнт передачі і ступінь загасання для
(т. 3,4 табл.30.3). Там же приведені результати розрахунку при сумісних обмеженнях на коефіцієнт передачі і ступінь загасання для 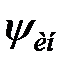 ПІД-регулятора (т. 5,6 табл.30.3) і ПІДД2-регулятора (т.7. табл.30.3).
ПІД-регулятора (т. 5,6 табл.30.3) і ПІДД2-регулятора (т.7. табл.30.3).
Характер перехідних процесів в АСР з ПІД-регулятором при розглянутих обмеженнях показаний на рис.30.4.
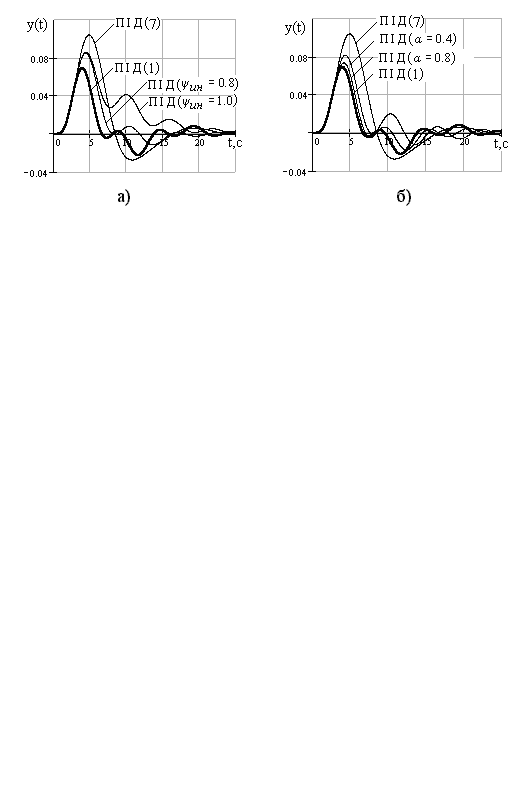
Рис.30.4. Перехідні процеси в АСР з ПІД-регулятором
а) оптимальна настройка 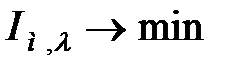 з обмеженням на
з обмеженням на 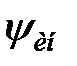 ;
;
б) оптимальна настройка 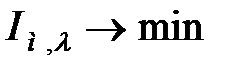 з обмеженням на
з обмеженням на 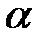 .
.
Оптимізація АСР по критерію 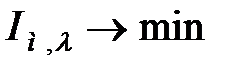 для стабілізуючих АСР в значній мірі знижує якість регулювання при збуреннях за завданням
для стабілізуючих АСР в значній мірі знижує якість регулювання при збуреннях за завданням 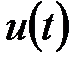 . Проте бажаний вид перехідних процесів може бути отриманий при використанні інтегруючих задатчиков.
. Проте бажаний вид перехідних процесів може бути отриманий при використанні інтегруючих задатчиков.
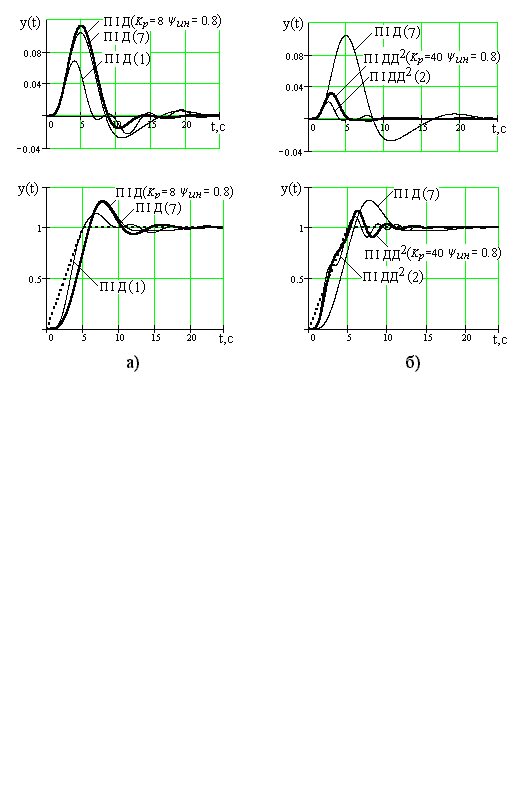
Рис.30.5. Перехідні процеси в АСР з інтегруючим задатчиком (пунктирна лінія) а) АСР з ПІД-регулятором; б) АСР с ПІДД2-регулятором.
На рис. 30.5 а показані процеси в АСР з ПІД-регулятором при обмеженнях на 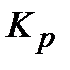 і
і 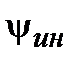 , і в АСР з ПІДД2-регулятором при аналогічних обмеженнях (рис. 5 б). Пунктирною лінією на рис.30.5 показаний сигнал на виході інтегруючого задатчика.
, і в АСР з ПІДД2-регулятором при аналогічних обмеженнях (рис. 5 б). Пунктирною лінією на рис.30.5 показаний сигнал на виході інтегруючого задатчика.
Настройки регуляторів, отримані при обмеженнях на параметри і показники запасу стійкості, з одного боку призводять до зниження якості АСР, з іншого боку роблять її робастною.
На закінчення слід зазначити, що запропонована методика дозволяє проводити для об'єктів з відомими динамічними характеристиками передпроектні дослідження і видавати рекомендації про доцільність використання в одноконтурних АСР багатопараметричних регуляторів.
Аналіз проведених досліджень дозволяє зробити висновок про те, що перехід від ПІД до ПІДД2-алгоритму дає помітний виграш. Так, для розглянутого прикладу величини відношення лінійного інтегрального критерію 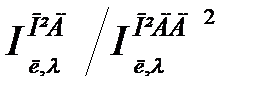 і інтегрального критерію по модулю
і інтегрального критерію по модулю 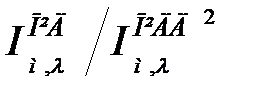 для варіантів 1,2 (табл.30.2) відповідно рівні 5 і 7, а в порівнянні з ПІД-регулятором, настроєним по даним [1], 8 і 13.
для варіантів 1,2 (табл.30.2) відповідно рівні 5 і 7, а в порівнянні з ПІД-регулятором, настроєним по даним [1], 8 і 13.
Дата добавления: 2017-08-01; просмотров: 309;
