ЛЕКЦІЯ 29 Синтез дискретних систем за допомогою логарифмічних характеристик

На W площини синтез дискретних систем по логарифмічних характеристиках здійснюється, так само як і для безперервних:

1. По методиках, відомих з теорії безперервних систем, будуємо логарифмічну амплітудно-частотну характеристику бажаної системи 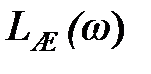Оскільки у всьому діапазоні істотних частот виконується співвідношення 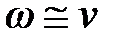, то маємо ;

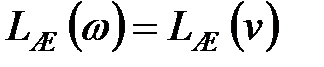2. Будуємо логарифмічну амплітудно-частотну характеристику наявної системи 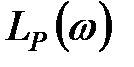. При правильно вибраному 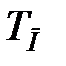у всьому діапазоні істотних частот так само повинне виконуватися співвідношення 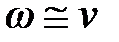і тому ;

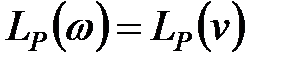3. Визначаємо послідовний коректуючий пристрій у функції абсолютної псевдочастоти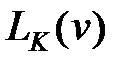

;

4. Використовуючи асимптотичну властивість логарифмічних характеристик імпульсних систем, побудованих у функції абсолютної псевдочастоти, визначаємо передаточну функцію послідовного коректуючого пристрою на W – площини;

5. Використовуючи підстановку 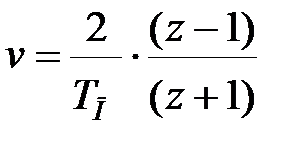, визначаємо 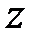-передаточну функцію коректуючого пристрою.

Застосуємо приведену методику до синтезу дискретної системи.

Приклад 29.1. Передаточна функція наявної системи задана рівнянням

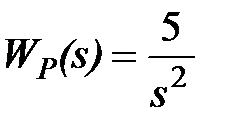
(29.1)

Перейдемо від безперервної передаточної функції об'єкту до Z-передаточної функції. Задамося інтервалом дискретності 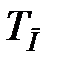і введемо запам'ятовуючий елемент нульового порядку. При прийнятих положеннях вираз (29.1) приймає вигляд

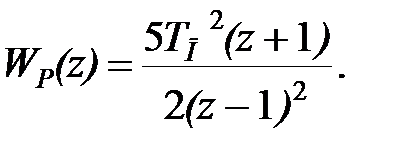
(29.1)

За допомогою підстановки 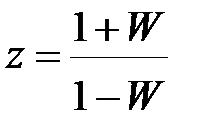переходимо на W площину і після введення абсолютної псевдочастоти 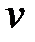отримаємо

(29.2)

За виразом (29.2) можна побудувати ЛАЧ характеристики імпульсних систем асимптотичним методом, а можна отримати необхідні характеристики за допомогою програми MatLab.

ЛАЧ характеристики наявної безперервної системи, побудованої у функції кругової частоти (h1A), і ЛАЧ характеристики її дискретного аналога (hA), побудованого у функції абсолютної псевдочастоти, представлені на рис.29.1. З характеристик рис. 29.1 видно, що в області істотних частот виконання умови 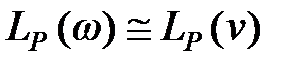. Отже, параметр 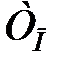вибраний правильно. Якби характеристики h1A і hA в області істотних частот відрізнялися, то слід було б зменшити 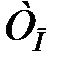і повторити розрахунки.

Як було вказано раніше працювати з фазовими характеристиками дискретних систем, побудованих програмами MatLab у функції псевдочастоти, важко. Про це свідчать і фазові характеристики, представлені на рис.29.1: криві hФ і h1Ф мають різні початки відліків.

Рис.29.1. ЛАЧ характеристики наявних систем

Вимоги до бажаних властивостей проектованої системи можуть бути задані графіками (бажаними логарифмічними характеристиками) або аналітично (передаточними функціями). Для системи, налаштованої на симетричний оптимум, передаточна функція бажаної системи має вигляд

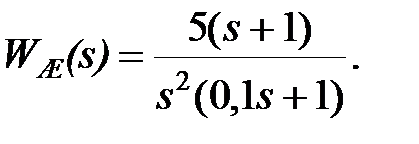
(29.3)

Враховуючи співвідношення 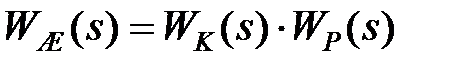отримуємо передаточну функцію коректуючого пристрою у функції кругової частоти

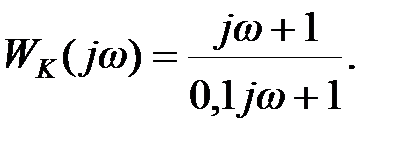
(29.4)

Оскільки на ділянці середніх частот виконується співвідношення , то характеристика дискретного коректуючого пристрою, у функції абсолютної псевдочастоти повинна визначатися виразом, співпадаючим з виразом (29.4)

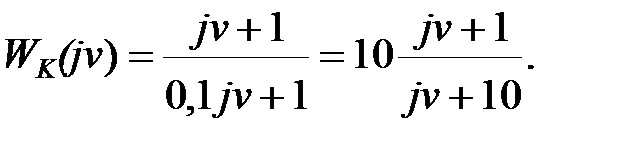
(29.5)

Для реалізації виразу (29.5) на Z - площині необхідно виконати ряд перетворень: від абсолютної псевдочастоти перейти до відносної псевдочастоти, а потім записати отримані вирази на площині Z

;

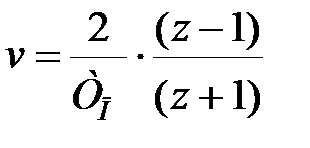При отримаємо:

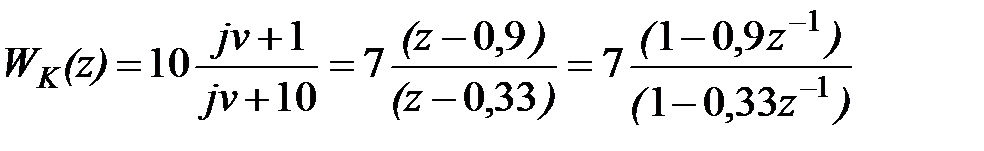
(29.6)

Коректуючий пристрій (29.5) має ділянку з нахилом +20 дб/дек, що дорівнює одній декаді: диференціювання починається при 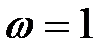рад/сек, а закінчується при 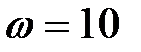рад/сек. Діапазон диференціювання можна збільшити до двох декад, використовуючи передаточну функцію

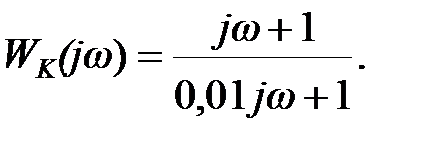
(29.7)

Дискретний коректуючий пристрій відповідний виразу (29.7), буде отриманий, якщо до нього застосувати перетворення (29.5) і (29.6)

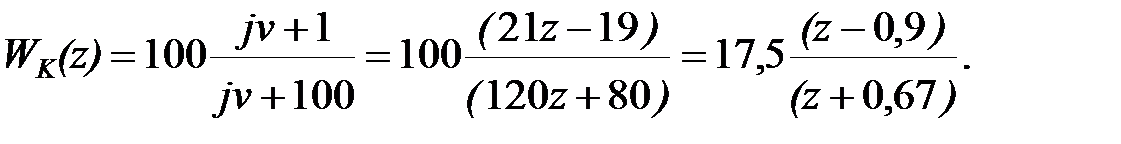
(29.8)

Близькість перехідних характеристик систем (безперервних і дискретних) свідчить про задовільну якість методики синтезу. Якщо прийняти аналогову систему за еталон, то в дискретних системах, що синтезуються, перехідні характеристики можуть мати навіть менше перерегулювання, що пояснюється правильним вибором діапазону диференціювання. Оскільки методика не дає чітких вказівок про вибір частот диференціюючих ланок, то їх параметри коректуються результатами моделювання.

Введення блоку, що запам'ятовує, збільшує перерегулювання в порівнянні з безперервною системою. Проте з введенням коректуючого пристрою (29.7) який, в порівнянні з коректуючим пристроєм (29.6), розширює діапазон диференціювання на одну декаду, вдається підвищити якість регулювання.

Розглянемо ще один приклад. Задана цифрова система, відповідна структурі рис.29.2.

Рис.29.2. Структурна схема імпульсної системи

Частина наявної системи регулювання задана безперервною передаточною функцією

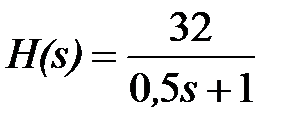
і дискретною, що реалізовує роботу інтегратора

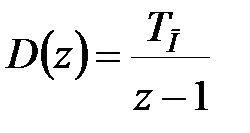
(29.9)

Для вибору дискретного коректуючого пристрою, необхіднийо вираз (29.9) записати у функції абсолютної псевдочастоти

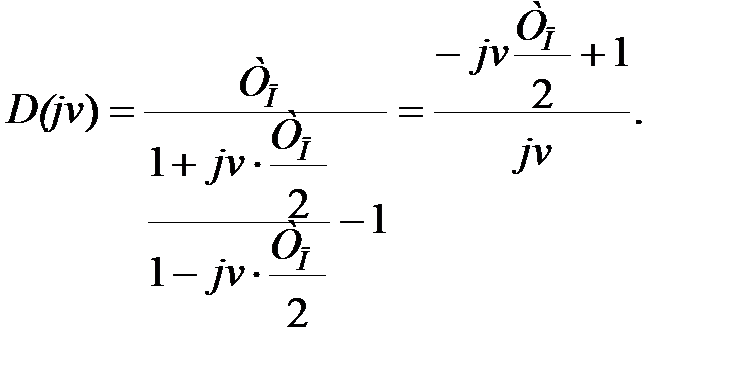
Інтервал дискретності 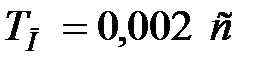вибраний правильно і в області істотних частот ЛАЧ характеристики дискретного інтегратора співпадають з характеристиками безперервного інтегратора. Тоді передаточна функція наявної частини системи, з урахуванням передаточної функції ЦОМ, описується виразом

.

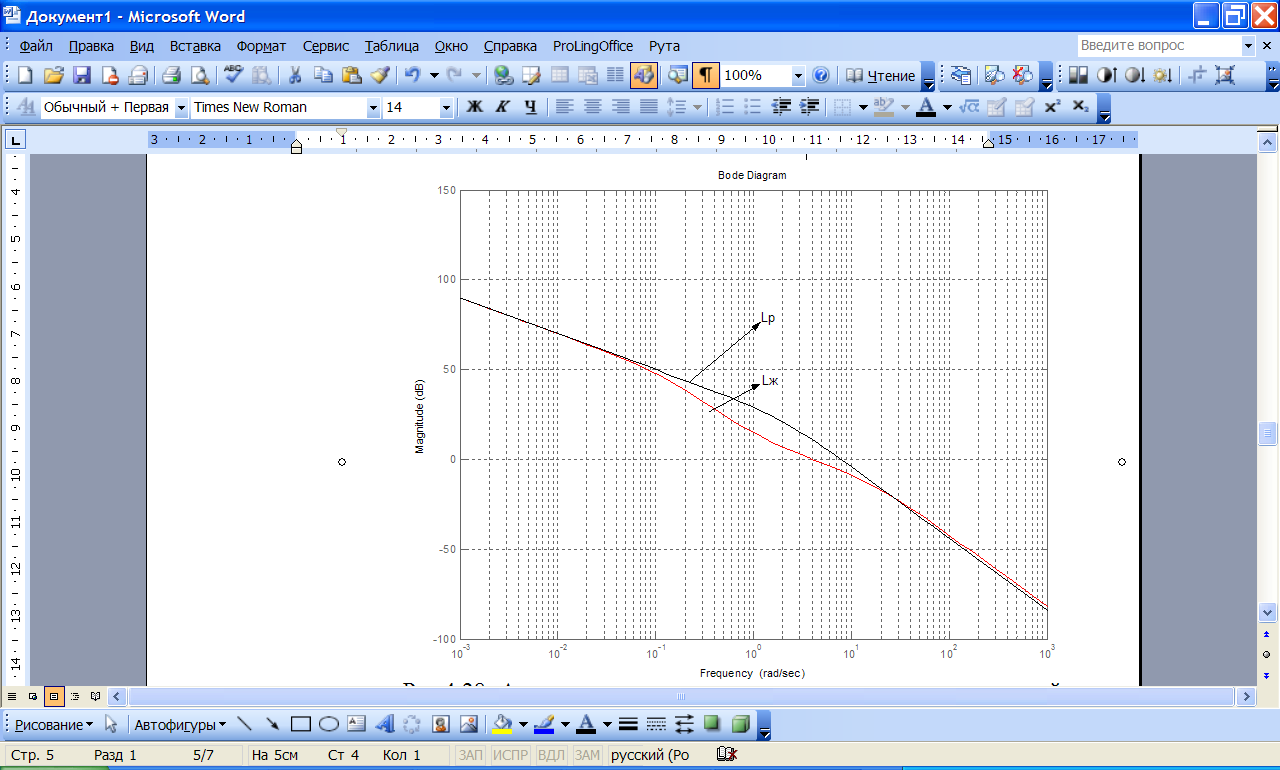
Рис.29.3. Амплітудно-частотні характеристики проектованої системи:
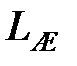- амплітудно-частотна характеристика бажаної системи;
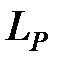- амплітудно-частотна характеристика наявної системи

На рис.29.3 представлені ЛАЧ характеристики, що дозволяють визначити дискретний коректуючий пристрій.

Оскільки ЛАЧ характеристики безперервної і дискретної системи в області істотних частот при 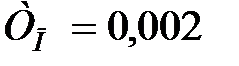співпадають, то послідовний коректуючий пристрій, визначається виразом 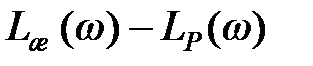. Виходячи з частот сполучення знаходимо передаточну функцію коректуючого пристрою

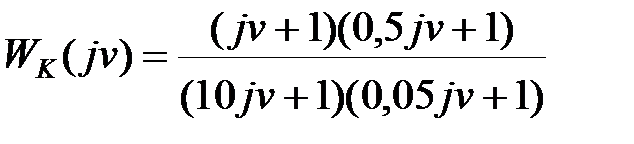
(29.10)

Здійснюємо у виразі (29.10) підстановку 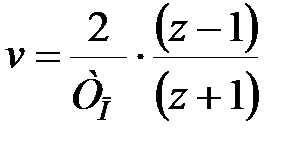і записуємо Z-передаточну функцію коректуючої ланки на Z площини

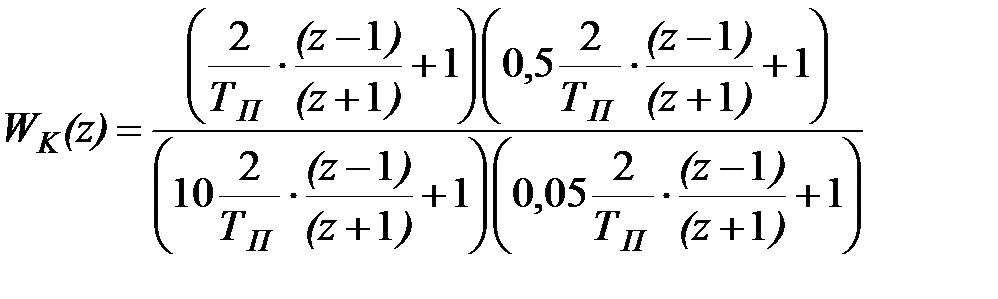
(29.11)

Слід зазначити, що характеристики системи регулювання істотно залежать від кількості значущих цифр, що представляють Z-передаточні функції. Дослідимо це питання і вираз (29.11) приведемо до наступного вигляду

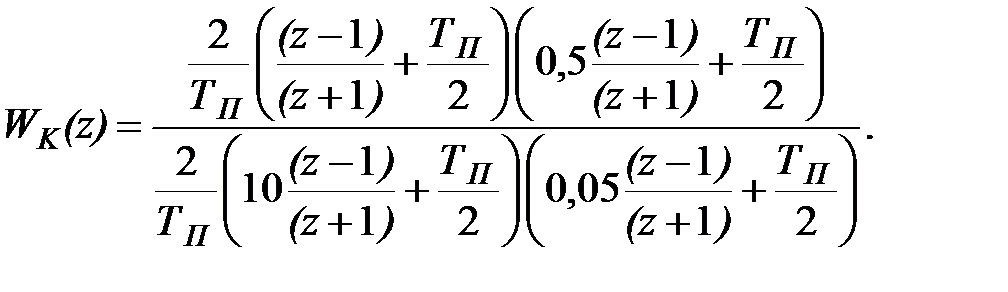
(29.12)

Оскільки 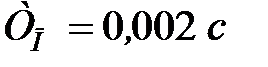, то в останньому виразі відкинемо другий доданок.

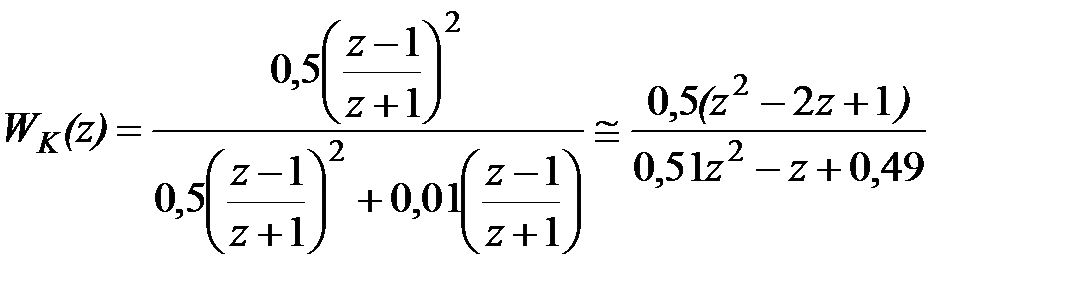
(29.13)

Вираз (29.13) визначає передаточну функцію коректуючого пристрою, без урахування ЦОМ. Знаючи передаточну функцію ЦОМ, визначену з урахуванням спрощень, повна передаточна функція коректуючого пристрою є

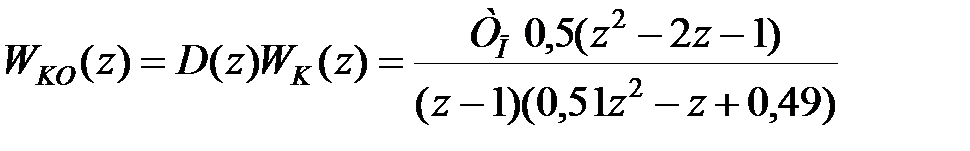
(29.14)

Розкриємо вираз (29.14) без спрощень чисельника. З урахуванням передаточної функції ЦОМ він приймає вигляд

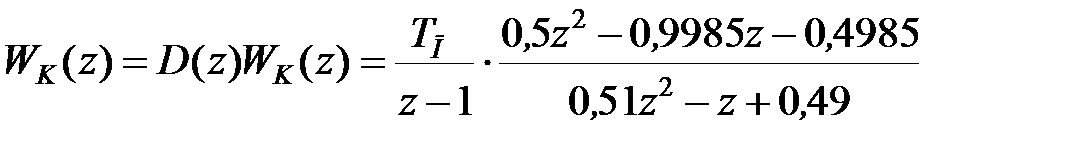
(29.15)

Порівняння виразів (29.14) і (29.15) показує, що поліном чисельника виразу (29.14) трохи відрізняється від полінома чисельника виразу (29.15). Проте ця відмінність істотно впливає на статичні і динамічні характеристики системи регулювання.

Таким чином, при розрахунках дискретних систем слід використовувати більшу кількість значущих цифр, чим при розрахунках безперервних систем, що слід враховувати не тільки при проектуванні, але і при реалізації цифрових пристроїв.