ЛЕКЦІЯ 28 синтез дискретних систем Методом поліноміальних рівнянь
Розглядається завдання синтезу при довільній (нефіксованій) структурі в наступній постановці. Задана передаточна функція приведеної безперервної частини  і відома дискретна передаточна функція незмінної частини
і відома дискретна передаточна функція незмінної частини
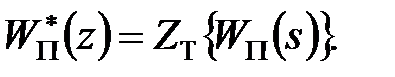
|
Відома також бажана передаточна функція 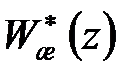 . Потрібно синтезувати регулятор, при якому передаточна функція
. Потрібно синтезувати регулятор, при якому передаточна функція 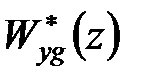 синтезованої системи (див. рис. 27.1) була б рівна бажаній:
синтезованої системи (див. рис. 27.1) була б рівна бажаній:
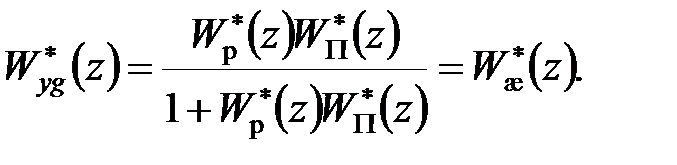
| (28.1) |
Вирішивши цю тотожність щодо передаточної функції регулятора, отримаємо
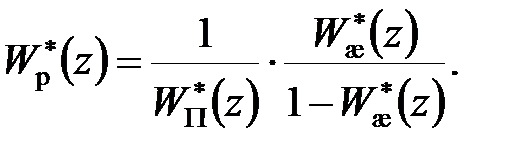
| (28.2) |
При синтезі регулятора потрібно забезпечити, щоб він був фізично здійснимим і синтезована система була грубою.
Умова фізичної здійсненності регулятора, що полягає в тому, що слідство не може передувати причині, може бути сформульоване таким чином: вагова функція регулятора дорівнює нулю при від’ємних аргументах або ступінь чисельника його передаточної функції не перевищує ступінь її знаменника.
При визначенні передаточної функції регулятора за формулою (28.2) синтезована система буде негрубою, якщо передаточна функція незмінної частини містить нулі або полюси поза одиничним кругом, і вони входять в передаточну функцію регулятора. В цьому випадку при обчисленні передаточної функції розімкненої системи вказані нулі і полюси скорочуються, якщо регулятор реалізується точно відповідно до (28.2). Проте при малій зміні параметрів регулятора вказані нулі і полюси можуть не скоротитися. Тоді розімкнена система стає нестійкою, що може привести до нестійкості і замкнутої системи.
Розкладемо чисельник і знаменник передаточної функції незмінної частини на два множники, один з яких містить нулі усередині одиничного кола, інший – на і поза одиничним колом:

|
Тут 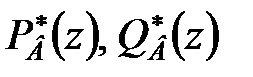 – поліноми, нулі яких розташовані усередині одиничного кола;
– поліноми, нулі яких розташовані усередині одиничного кола; 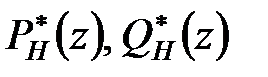 – поліноми, нулі яких розташовані на і поза одиничним колом.
– поліноми, нулі яких розташовані на і поза одиничним колом.
Підставимо отриманий вираз для  у (28.2):
у (28.2):
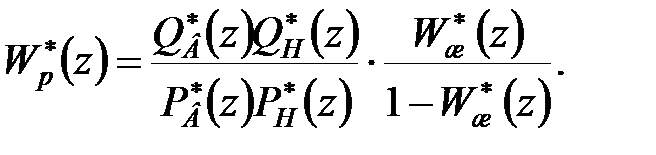
| (28.3) |
Як наголошувалося, для того, щоб синтезована система була грубою, передаточна функція регулятора (28.3) не повинна містити поліноми 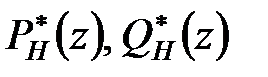 , що містять нулі поза одиничним колом.
, що містять нулі поза одиничним колом.
Але, як це витікає з (28.3), для цього потрібно, щоб 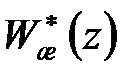 включала поліном
включала поліном  а
а 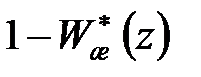 – поліном
– поліном 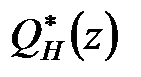 тобто бажана передаточна функція повинна задовольняти співвідношенням
тобто бажана передаточна функція повинна задовольняти співвідношенням
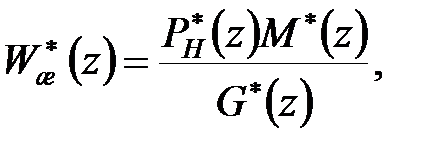
| (28.4а) |

| (28.4б) |
де 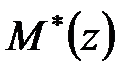 і
і  – невизначені поліноми;
– невизначені поліноми;  – знаменник бажаної передаточної функції, тобто характеристичний поліном системи, що синтезується; множник
– знаменник бажаної передаточної функції, тобто характеристичний поліном системи, що синтезується; множник  вводиться для забезпечення необхідного порядку астатизму.
вводиться для забезпечення необхідного порядку астатизму.
Виключивши 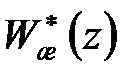 з (28.4), отримаємо поліноміальне рівняння
з (28.4), отримаємо поліноміальне рівняння
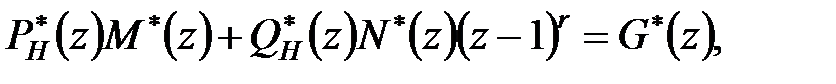
| (28.5) |
звідки визначаються поліноми 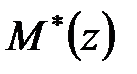 і
і  .
.
Підставивши (28.4а), (28.4б) в (28.3), знаходимо
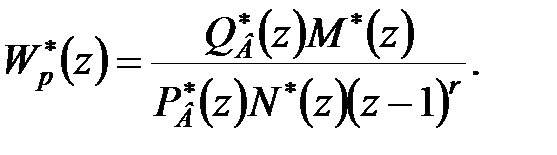
| (28.6) |
Позначимо ступінь довільного полінома 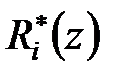 через
через 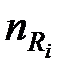 . Тоді умову фізичної здійсненності регулятора з (28.6) можна записати у вигляді
. Тоді умову фізичної здійсненності регулятора з (28.6) можна записати у вигляді
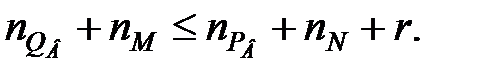
| (28.8) |
Поліноміальне рівняння (28.5) вирішуване, якщо число невідомих (коефіцієнтів поліномів 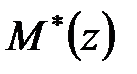 і
і  не менше числа рівнянь, отримуваних прирівнюванням коефіцієнтів при однакових ступенях в рівнянні (28.5). І так як число невідомих дорівнює
не менше числа рівнянь, отримуваних прирівнюванням коефіцієнтів при однакових ступенях в рівнянні (28.5). І так як число невідомих дорівнює 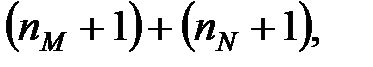 а число рівнянь
а число рівнянь 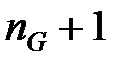 умова вирішення поліноміального рівняння приймає вигляд
умова вирішення поліноміального рівняння приймає вигляд
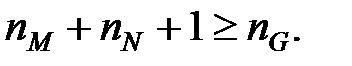
| (28.8) |
У (28.4б) ступені поліномів чисельника і знаменника рівні. Тому з його правої частини маємо 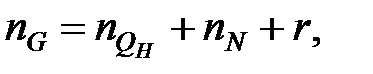 звідки
звідки
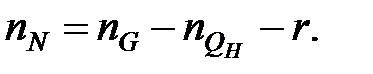
| (28.9) |
Об'єднуючи умову фізичної здійсненності (28.7) і умову вирішуванності (28.8), з урахуванням (28.9) отримаємо
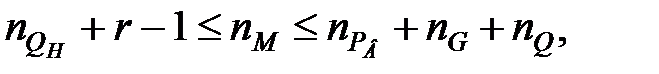
| (28.10) |
де 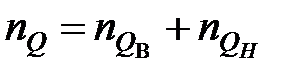 – ступінь знаменника передаточної функції незмінної частини.
– ступінь знаменника передаточної функції незмінної частини.
Таким чином, умови фізичної здійсненності регулятора і вирішуванності поліноміального рівняння будуть виконані, якщо ступені поліномів 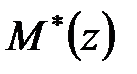 і
і  задовольняють співвідношенням (28.9) і (28.10).
задовольняють співвідношенням (28.9) і (28.10).
З умови (28.10) отримуємо, що ступінь характеристичного полінома системи, що синтезується, повинен задовольняти нерівності
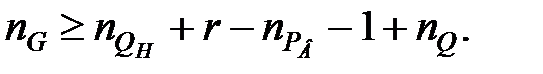
| (28.11) |
Хоча спочатку ми припускали, що бажана передаточна функція відома, насправді вона не може бути вибрана заздалегідь.
Порядок синтезу системи управління методом поліноміальних рівнянь можна сформулювати таким чином.
1. Розкласти поліноми чисельника і знаменника передаточної функції незмінної частини на два множники, один з яких має нулі усередині одиничного кола, інший – на і зовні одиничного кола. Якщо вказані поліноми не мають нулів на і поза одиничним колом, то покласти 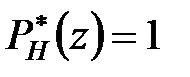 і
і 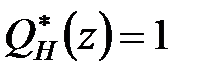 , якщо вони не мають нулів усередині одиничного кола, то прирівняти
, якщо вони не мають нулів усередині одиничного кола, то прирівняти 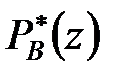 і
і 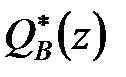 постійному множнику цих поліномів.
постійному множнику цих поліномів.
2. Виходячи з вимог до якості системи, що синтезується, в перехідному режимі і порядку астатизма вибрати характеристичний поліном системи, що синтезується  і число
і число  . Ступінь полінома
. Ступінь полінома  повинна задовольняти умові (28.11).
повинна задовольняти умові (28.11).
3. Із співвідношень (28.9) і (28.10) визначити ступені невизначених поліномів 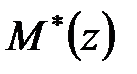 і
і  і записати їх з невизначеними коефіцієнтами.
і записати їх з невизначеними коефіцієнтами.
4. Підставити отримані невизначені поліноми в поліноміальне рівняння і визначити їх коефіцієнти.
5. Підставити знайдені поліноми 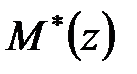 і
і  у формулу для передаточної функції регулятора (28.6).
у формулу для передаточної функції регулятора (28.6).
Приклад 28.1. Передаточна функція незмінної частини 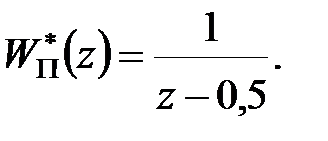 Потрібно синтезувати регулятор, при якому статична помилка дорівнює нулю і перехідний процес закінчується за кінцеве число кроків.
Потрібно синтезувати регулятор, при якому статична помилка дорівнює нулю і перехідний процес закінчується за кінцеве число кроків.
Рішення. В даному випадку 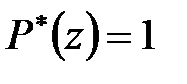 і
і 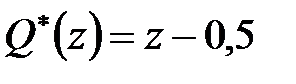 і відповідно
і відповідно 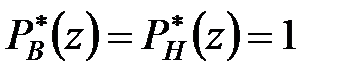 і
і  і
і 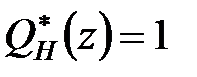 . Ступені поліномів
. Ступені поліномів 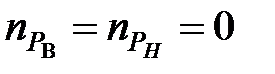 ,
, 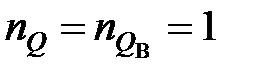 ,
, 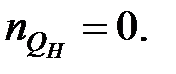
Оскільки статична помилка повинна дорівнювати нулю, покладемо 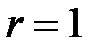 . Умова (28.11) приймає вигляд
. Умова (28.11) приймає вигляд 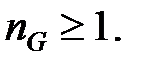 Покладемо
Покладемо 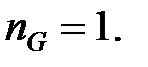 І, щоб перехідний процес закінчився за кінцеве число кроків, вважаємо характеристичний поліном
І, щоб перехідний процес закінчився за кінцеве число кроків, вважаємо характеристичний поліном 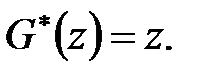
Умови (28.9) і (28.10) приймають вигляд 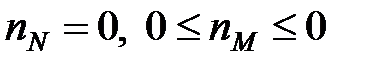 .
.
Тому вважаємо 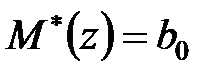 і
і 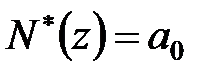 . Підставивши їх в поліноміальне рівняння (28.5), отримаємо
. Підставивши їх в поліноміальне рівняння (28.5), отримаємо 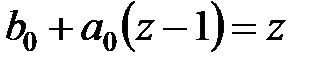 .
.
Прирівнявши коефіцієнти при однакових ступенях, знаходимо 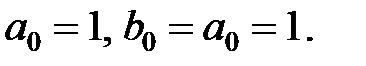
Отже 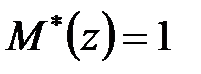 і
і 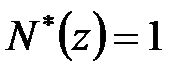 . Підставивши ці вирази для
. Підставивши ці вирази для 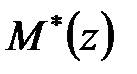 і
і 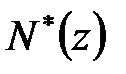 а також вирази для
а також вирази для 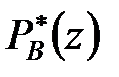 і
і  у (28.6), отримаємо шукане рішення
у (28.6), отримаємо шукане рішення 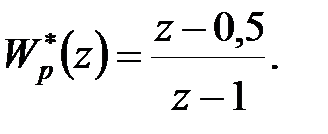
Приклад 28.2. Передаточна функція незмінної частини 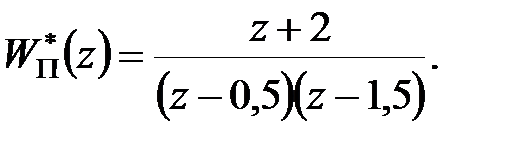
Потрібно синтезувати регулятор, при якому статична помилка дорівнює нулю і перехідний процес закінчується за кінцеве число кроків.
Рішення. В даному випадку 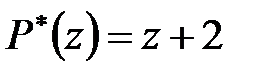 і
і 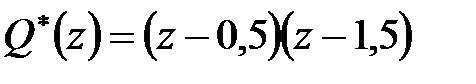 і, відповідно,
і, відповідно, 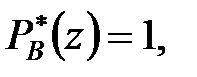
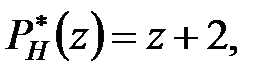
 і
і 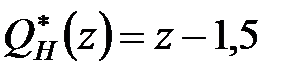 . Ступені поліномів:
. Ступені поліномів: 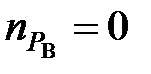 ,
, 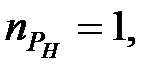
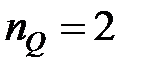 ,
, 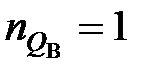 ,
, 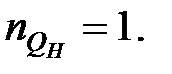
Оскільки статична помилка повинна дорівнювати нулю, покладемо 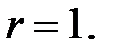 Умова (28.11) приймає вигляд
Умова (28.11) приймає вигляд 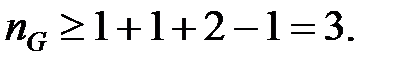 Покладемо
Покладемо 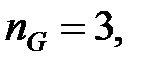 і для того, щоб перехідний процес закінчився за кінцеве число кроків, вважаємо характеристичний поліном
і для того, щоб перехідний процес закінчився за кінцеве число кроків, вважаємо характеристичний поліном 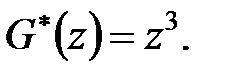 Умови (28.9) і (28.10) приймають вигляд
Умови (28.9) і (28.10) приймають вигляд 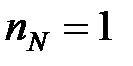 ,
, 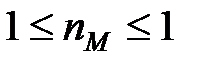 .
.
Тому вважаємо 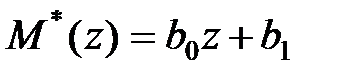 і
і 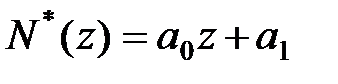 . Підставивши їх в поліноміальне рівняння (28.5), отримаємо
. Підставивши їх в поліноміальне рівняння (28.5), отримаємо
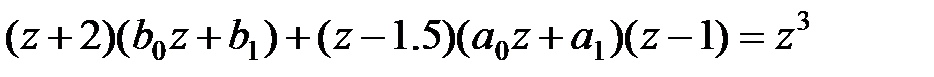 ,
,
або, після розкриття дужок і приведення подібних членів
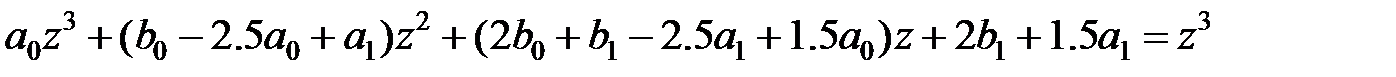
Прирівнявши коефіцієнти при однакових ступенях, знаходимо 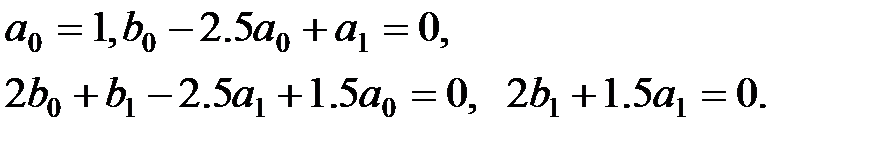
Вирішивши цю систему, отримаємо 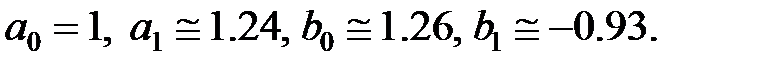
Отже 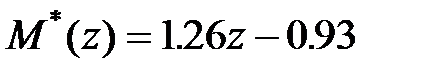 і
і 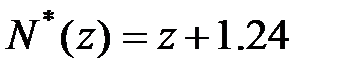 Підставивши ці вирази для
Підставивши ці вирази для 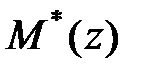 і
і 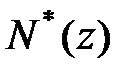 , а також вирази для
, а також вирази для 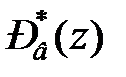 і
і 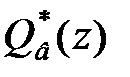 у (28.6), отримаємо шукане рішення
у (28.6), отримаємо шукане рішення
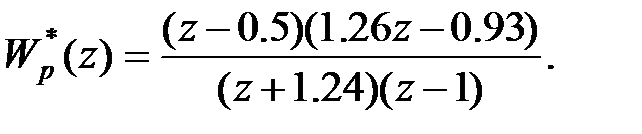
Синтез дискретної системи по безперервній моделі.
Дискретний регулятор можна конструювати, використовуючи методи синтезу безперервних систем. Для цього спочатку потрібно за допомогою вказаних методів визначити передаточну функцію 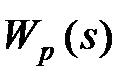 аналогового (безперервного) регулятора, а потім апроксимувати
аналогового (безперервного) регулятора, а потім апроксимувати 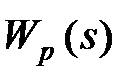 дискретною передаточною функцією
дискретною передаточною функцією 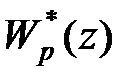 При цьому, враховуючи, що дискретизація за часом з періодом
При цьому, враховуючи, що дискретизація за часом з періодом 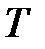 вводить запізнювання
вводить запізнювання 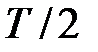 , слід проводити синтез для об'єкту з передаточною функцією
, слід проводити синтез для об'єкту з передаточною функцією 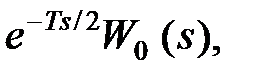 де
де 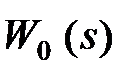 – передаточна функція початкового об'єкту. При синтезі передаточну функцію введеної ланки чистого запізнювання можна апроксимувати одним з наступних способів:
– передаточна функція початкового об'єкту. При синтезі передаточну функцію введеної ланки чистого запізнювання можна апроксимувати одним з наступних способів:
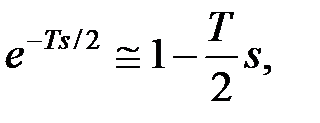
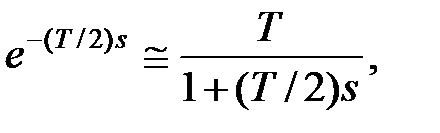
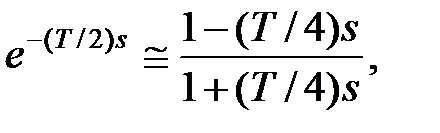
При отриманні дискретної передаточної функції 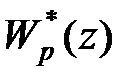 можна скористатися апроксимацією похідної кінцевими різницями (метод Ейлера): прямою
можна скористатися апроксимацією похідної кінцевими різницями (метод Ейлера): прямою
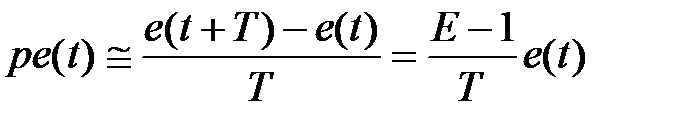 ,
,
або зворотною
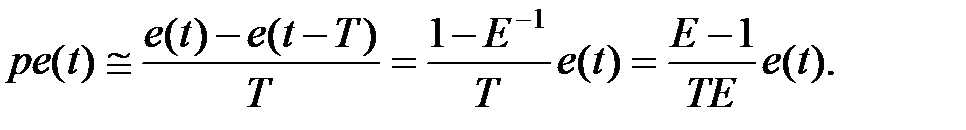
На основі цієї рівності використовуючи метод Ейлера s замінюється на 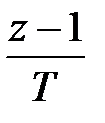 або
або 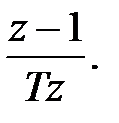
Інший метод апроксимації – метод трапеції, або метод Тустена (Tustin) – полягає в тому, що 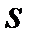 замінюється на
замінюється на 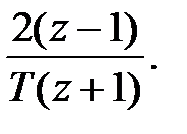 Така заміна отримуться наступним чином.
Така заміна отримуться наступним чином.
Інтеграл 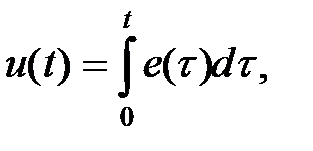 поклавши
поклавши 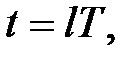 можна представити у вигляді
можна представити у вигляді
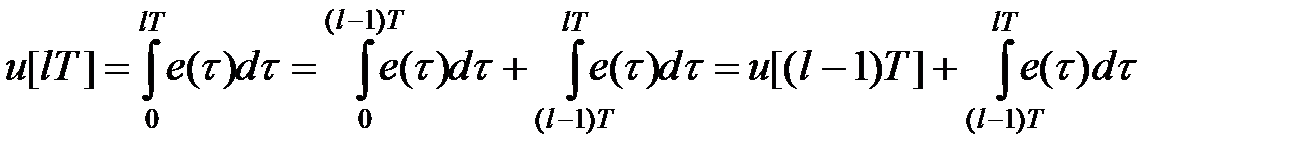
Останній інтеграл представляє площу під кривою 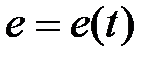 на відрізку
на відрізку 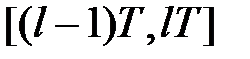 (рис. 28.1).
(рис. 28.1).
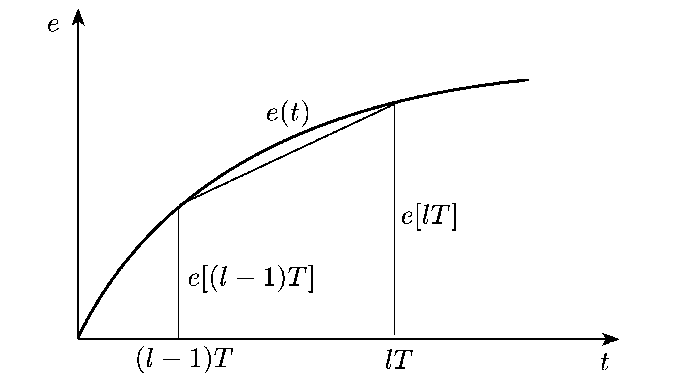
Рис. 28.1. Апроксимація трапецій
Замінивши цю площу площею трапеції, що отримується при апроксимації кривої 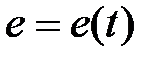 відрізком прямої на вказаному відрізку, знаходимо
відрізком прямої на вказаному відрізку, знаходимо
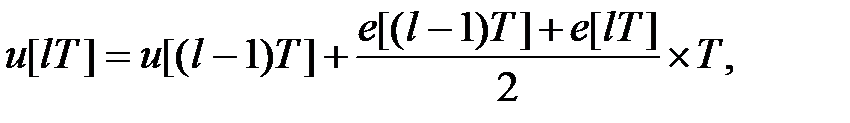
або, в операторній формі,
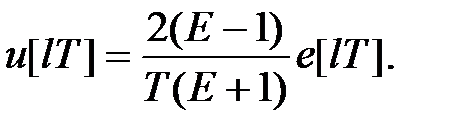
Це співвідношення отримане з рівності
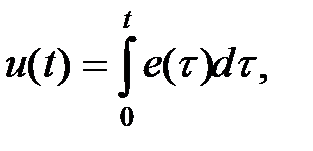 або
або 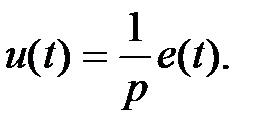
Порівнюючи останню рівність з попереднім співвідношенням, отримуємо, що диференціальному операторові 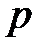 відповідає різницевий оператор
відповідає різницевий оператор 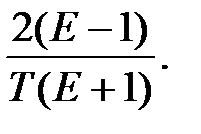 Тому при апроксимації аналогової передаточної функції дискретною методом трапеції
Тому при апроксимації аналогової передаточної функції дискретною методом трапеції  замінюється на
замінюється на 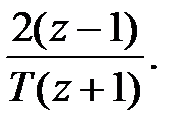
Дата добавления: 2017-08-01; просмотров: 252;
