Обчислення -зображення і -зображення
Для отримання дискретної моделі по еквівалентній схемі АІМ-системи необхідно визначити дискретну передаточну функцію 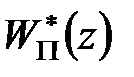 для чого відповідно до формули (20.13) потрібно виконати
для чого відповідно до формули (20.13) потрібно виконати 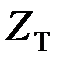 -перетворення передаточної ПБЧ.
-перетворення передаточної ПБЧ.
По аналогії з z-перетворенням в 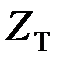 -перетворенні
-перетворенні
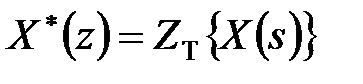 . .
|
і в 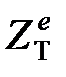 -перетворенні
-перетворенні
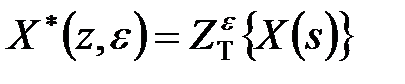 . .
|
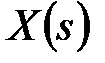 називатимемо оригіналом
називатимемо оригіналом 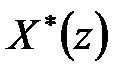 –
– 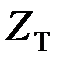 -зображенням і
-зображенням і 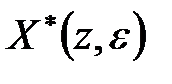 -зображенням або модифікованим
-зображенням або модифікованим 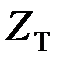 -зображенням.
-зображенням.
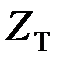 зображення і
зображення і 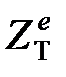 -зображення від основних функцій можна знайти відповідно в табл. 19.1 і табл. 19.2.
-зображення від основних функцій можна знайти відповідно в табл. 19.1 і табл. 19.2.
Обчислення 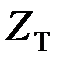 -зображення і
-зображення і 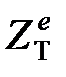 -зображення від дробно-раціональної функції. Хай оригінал має вигляд
-зображення від дробно-раціональної функції. Хай оригінал має вигляд
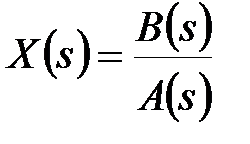 , ,
|
де 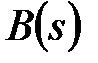 і
і 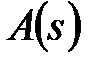 – поліноми від
– поліноми від 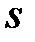 ступені
ступені 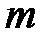 і
і 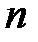 відповідно, причому
відповідно, причому 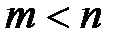 . Якщо всі полюси
. Якщо всі полюси 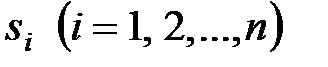 даної функції (тобто корені рівняння
даної функції (тобто корені рівняння 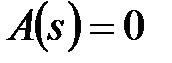 ) різні, то
) різні, то
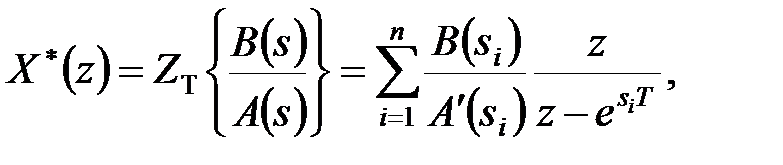
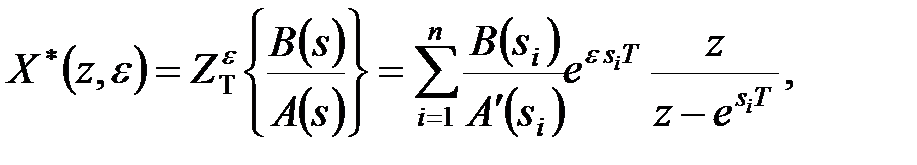
| (20.15) (20.16) |
де 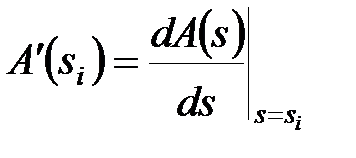 .
.
Формула (20.15) виходить з (20.16) як окремий випадок при 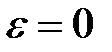 . А формула (20.16) виводиться наступним чином.
. А формула (20.16) виводиться наступним чином.
По формулі розкладання маємо
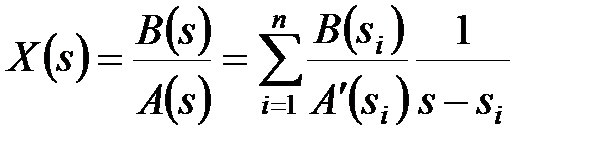 . .
|
Враховуючи властивість лінійності оператора 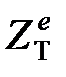 маємо
маємо
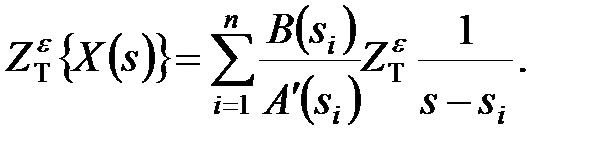
|
По табл. 19.2 (рядок 4) знаходимо
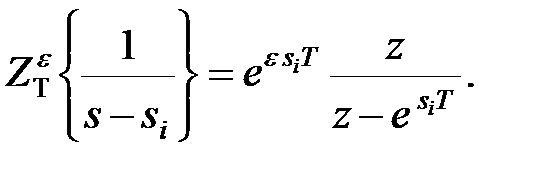
|
Підставивши цей вираз в попереднє співвідношення, отримаємо (20.16).
Приклад 20.1. Передаточна функція ПБЧ має вигляд 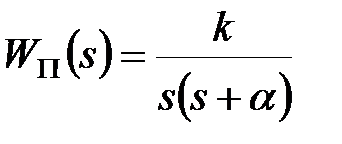 Потрібно знайти дискретну передаточну функцію
Потрібно знайти дискретну передаточну функцію 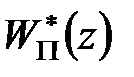 .
.
Рішення. Полюсами даної передаточної функції (тобто коренями рівняння 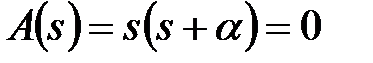 являються
являються 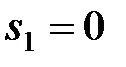
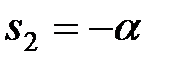
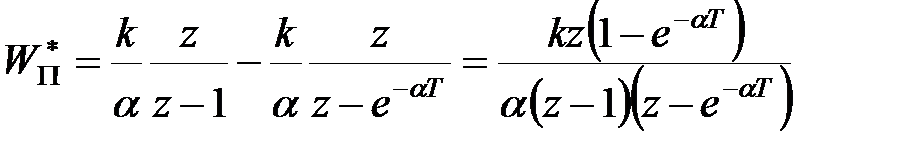 . .
|
Якщо 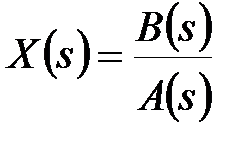 містить кратні полюси, то зображення
містить кратні полюси, то зображення 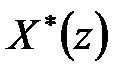 і
і 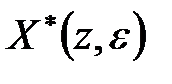 можна отримати, розклавши
можна отримати, розклавши 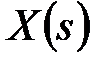 на елементарні дроби. У простих випадках можна введенням малих параметрів видозмінити функцію
на елементарні дроби. У простих випадках можна введенням малих параметрів видозмінити функцію 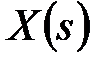 так, щоб вона не містила кратних полюсів, і скористатися формулами (20.15) і (20.16), а потім провести граничний перехід, спрямувавши малі параметри до нуля.
так, щоб вона не містила кратних полюсів, і скористатися формулами (20.15) і (20.16), а потім провести граничний перехід, спрямувавши малі параметри до нуля.
Пример 20.2. Передаточна функція приведеної безперервної частини має вигляд 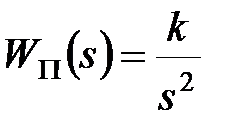 . Потрібно визначити дискретну передаточну функцію
. Потрібно визначити дискретну передаточну функцію 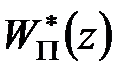 .
.
Дана передаточна функція приведеної безперервної частини має дворазовий полюс 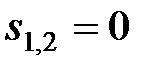 . Ввівши малий параметр
. Ввівши малий параметр 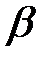 , перетворимо її до виду
, перетворимо її до виду
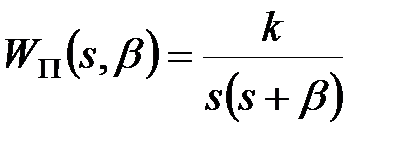 . .
|
Перетворена передаточна функція має прості полюси 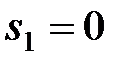 ,
, 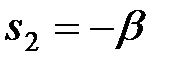 . Похідна
. Похідна 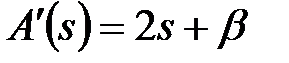 . За формулою (20.15) одержуємо
. За формулою (20.15) одержуємо
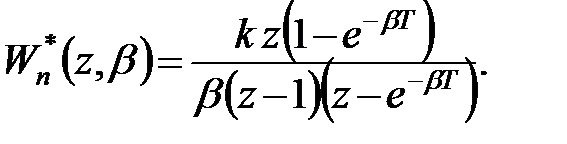
|
Використовуючи розкладання  , де
, де 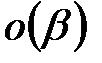 – нескінченно мала величина більш високого порядку, чим
– нескінченно мала величина більш високого порядку, чим 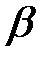 (тобто
(тобто 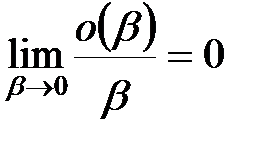 ), одержуємо
), одержуємо
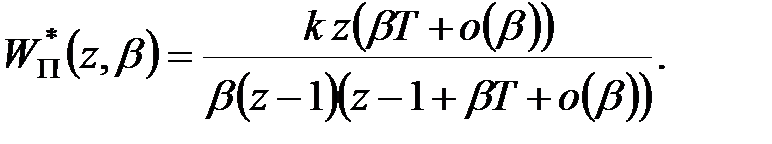
|
Звідси, спрямувавши 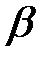 до нуля, знаходимо
до нуля, знаходимо
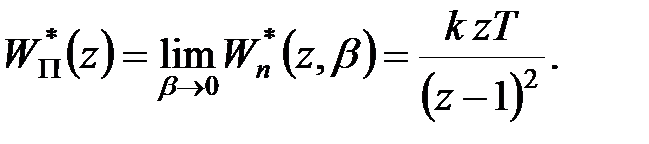
|
Якщо серед простих полюсів функції 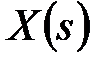 є комплексний корінь, то може виявитися недоцільним використання формул (20.15) і (20.16). Це пов'язане з необхідністю перетворення отриманого результату для виключення уявного числа. У всіх випадках, коли використання формул (20.15) і (20.16) неможливо або недоцільно, можна визначити
є комплексний корінь, то може виявитися недоцільним використання формул (20.15) і (20.16). Це пов'язане з необхідністю перетворення отриманого результату для виключення уявного числа. У всіх випадках, коли використання формул (20.15) і (20.16) неможливо або недоцільно, можна визначити 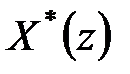 й
й 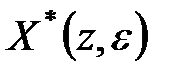 , розклавши
, розклавши 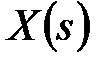 на елементарні дроби.
на елементарні дроби.
Приклад 20.3. АІМ-елемент виробляє прямокутні імпульси тривалості 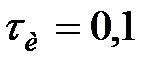 з періодом
з періодом 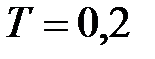 і амплітудою
і амплітудою 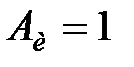 . Передаточна функція безперервної частини
. Передаточна функція безперервної частини 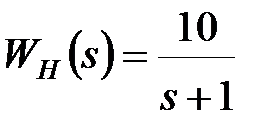 .
.
Потрібно визначити дискретну передаточну функцію 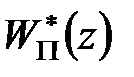 .
.
Рішення. Знайдемо спочатку передаточну функцію приведеної безперервної частини. Оскільки передаточна функція формуючої ланки
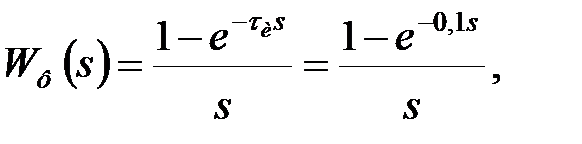
|
передаточна функція ПБЧ имеет вид
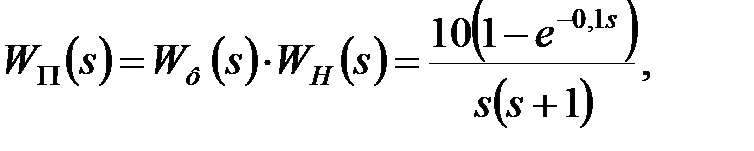
|
або
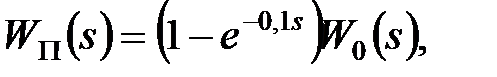
|
де 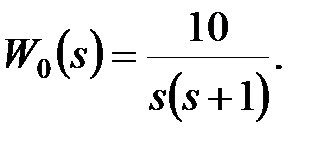
Дискретна передаточна функція
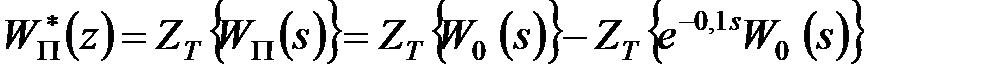 . .
|
В даному випадку 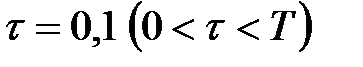 ,
, 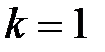 и
и 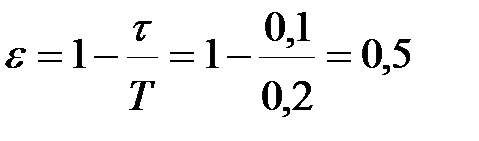 . Тому
. Тому
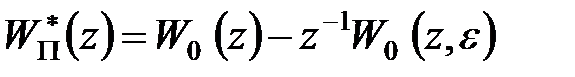 . .
|
Полюсами 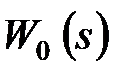 являються
являються 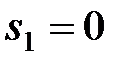 ,
, 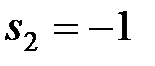 похідна
похідна 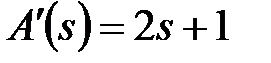 Відповідно до (20.15) і (20.16)
Відповідно до (20.15) і (20.16)
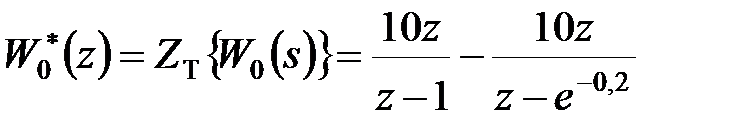 , ,
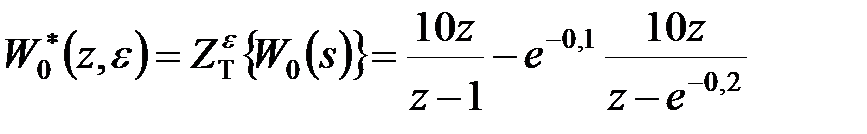 . .
|
Отже,
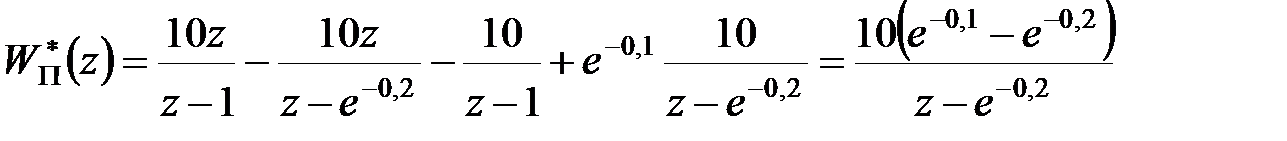 . .
|
Дата добавления: 2017-08-01; просмотров: 258;
