Дискретна модель АІМ-системи

Позначивши вагову функцію ПБЧ через 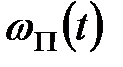маємо (см. рис. 20.3, б)

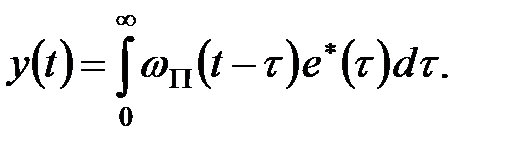
(20.7)

Підставивши вираз для 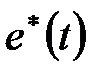з (20.4), після інтегрування отримаємо

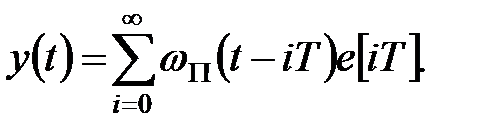
(20.8)

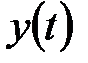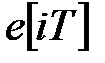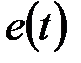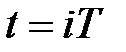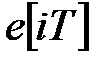З цього рівняння виходить, що вихідна змінна залежить від , тобто від значень у дискретні моменти часу Для маємо

.

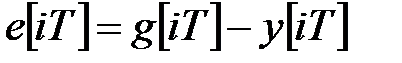(20.9)

У будь-який момент часу АІМ-система описується рівняннями (20.8) і (20.9). У рівняння (20.8) входять безперервні функції (функції з безперервними аргументами) 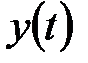і 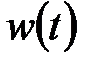, а також дискретна функція 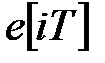. У рівняння (20.9) входять тільки дискретні функції. Таким чином, АІМ-система є безперервно-дискретною системою. І те, що вона описується рівняннями, в які входять дискретні і безперервні функції, доставляє незручність. Від цієї незручності можна позбавиться, якщо обмежитися дослідженням АІМ-системи тільки в дискретні моменти часу .

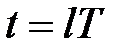Дійсно, підставивши в (20.8) 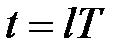отримаємо

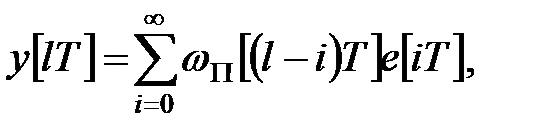
або, враховуючи, що 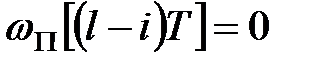при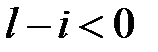

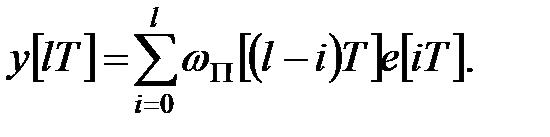
(20.10)

Рівняння (20.9) і (20.10) описують процеси в АІМ-системі в дискретні моменти часу і представляють її дискретну модель. Як побачимо далі, по дискретній моделі при необхідності можна визначити значення вихідної змінної 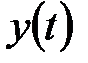не тільки в моменти часу 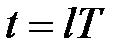але і в довільні моменти .

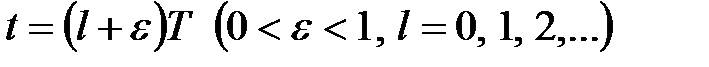Провівши 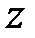-перетворення, з рівнянь (20.9) і (20.10) отримаємо

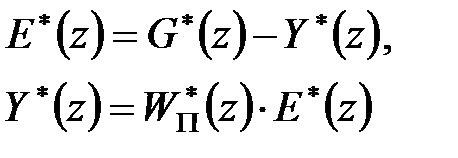
(20.11 а) (20.11 б)

де

.

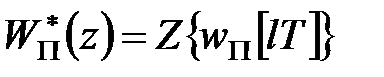(20.12)

Рівняння (20.11 б) отримане з використанням теореми про згортання.

З рівняння (20.11б) маєм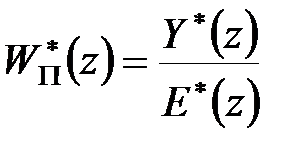о тобто 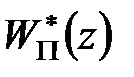є передаточна функція (у 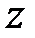-зображеннях) прямому ланцюгу з входоми 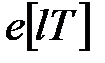і виходом .

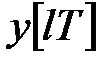На підставі рівнянь (20.11а), (20.11 б) можна побудувати структурну схему дискретної моделі АІМ-систем (рис. 20.4).

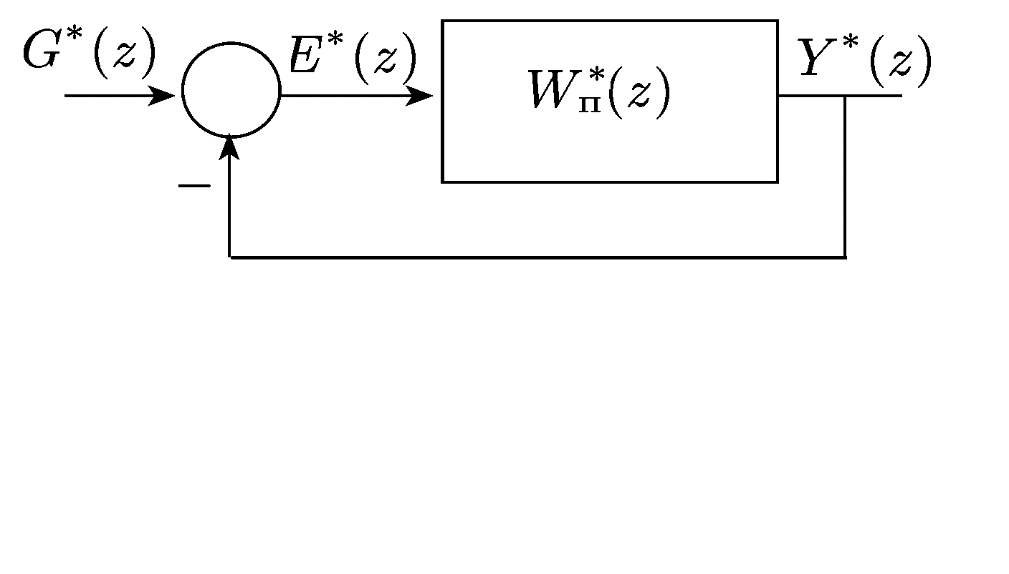
Рис. 20.4. Дискретна модель АІМ-системи

Передаточна функція замкнутої дискретної системи по цій структурній схемі визначається так само, як і у разі безперервних систем. Так, наприклад, передаточна функція щодо входу 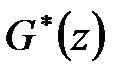і виходу 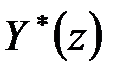має вигляд

,

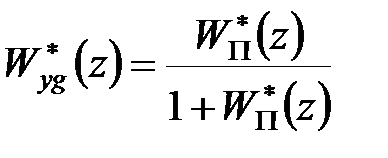а щодо входу 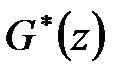і виходу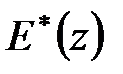

,

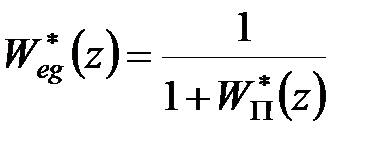Основна особливість розрахунку АІМ-системи полягає в обчисленні передаточної функції 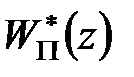по відомій передаточній функції ПБЧ 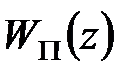, що рівнює добутку передаточних функцій формуючої ланки і безперервної частини.

Згідно формулі (20.11) 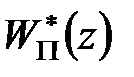є 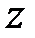-зображення вагової функції ПБЧ 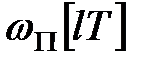. Вагову функцію 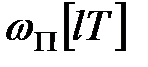можна отримати шляхом дискретизації за часом безперервної вагової функції 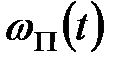яка виходить з передаточної функції .

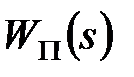Знаючи зв'язок між зображенням Лапласа безперервної функції і z-зображенням відповідної гратчастої функції, можна безпосередньо по 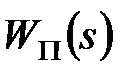визначити .

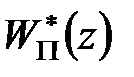Введемо в розгляд оператор 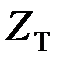який кожній функції 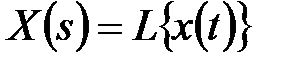ставить у відповідність функцію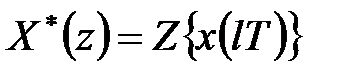

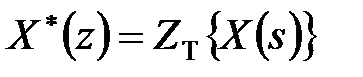
Оператор 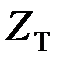відповідає трем послідовним операціям: зворотному перетворенню Лапласа, квантуванню за часом і 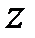-перетворенню. Оскільки всі три вказані операції є лінійними, то оператор 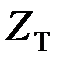є лінійним. Використовуючи цей оператор, передаточну функцію 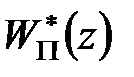можна визначити таким чином:

.

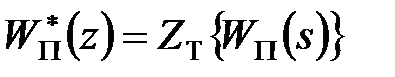(20.13)

Далі також використовуватимемо оператор 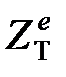який функції 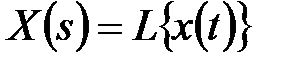ставить у відповідність модифіковане 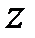-зображення :

.

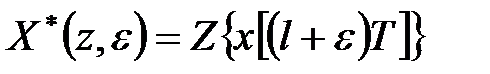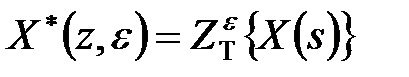(20.14)