Зображення основних функцій
У табл. 19.1 і табл. 19.2 представлені відповідно звичайні і модифіковані  -зображення основних гратчастих функцій. Гратчаста функція
-зображення основних гратчастих функцій. Гратчаста функція 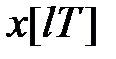 виходить шляхом квантування (дискретизації) за часом безперервної функції
виходить шляхом квантування (дискретизації) за часом безперервної функції 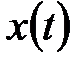 . Надалі потрібно буде обчислювати
. Надалі потрібно буде обчислювати 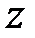 -зображення гратчастої функції по відомому зображенню Лапласа
-зображення гратчастої функції по відомому зображенню Лапласа 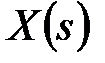 безперервної функції
безперервної функції 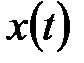 . І при цьому щоб уникнути етапів обчислення
. І при цьому щоб уникнути етапів обчислення 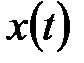 шляхом зворотного перетворення Лапласа і дискретизації, у вказаних таблицях в першому стовпці приведені зображення Лапласа відповідних безперервних функцій. Розглянемо виведення формул, приведених в табл. 19.1 і табл. 19.2. І так як формули для звичайних
шляхом зворотного перетворення Лапласа і дискретизації, у вказаних таблицях в першому стовпці приведені зображення Лапласа відповідних безперервних функцій. Розглянемо виведення формул, приведених в табл. 19.1 і табл. 19.2. І так як формули для звичайних  -зображень виходять з формул для модифікованих
-зображень виходять з формул для модифікованих 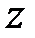 -зображень при
-зображень при 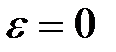 обмежимося виведенням формул, приведених в табл. 19.2.
обмежимося виведенням формул, приведених в табл. 19.2.
Таблиця 19.1.  -зображення
-зображення
| № | 
| 
| 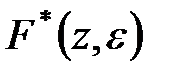
|
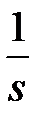
| 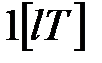
| 
| |
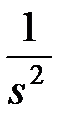
| 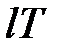
| 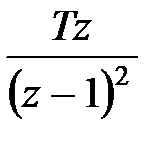
| |
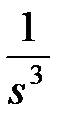
| 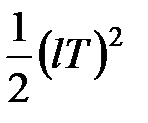
| 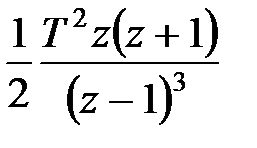
| |
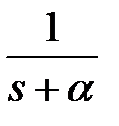
| 
| 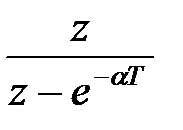
| |

| 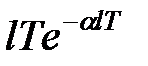
| 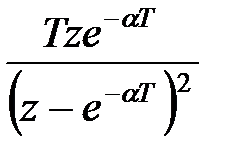
| |
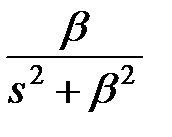
| 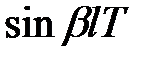
| 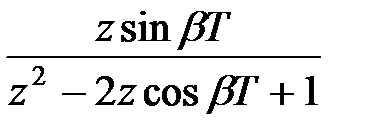
| |
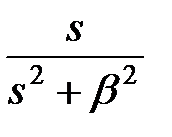
| 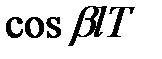
| 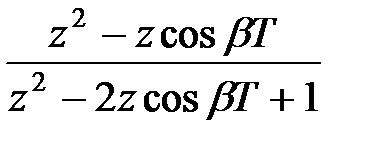
| |
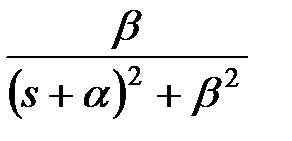
| 
| 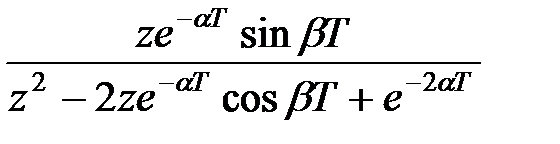
| |
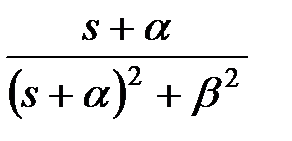
| 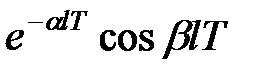
| 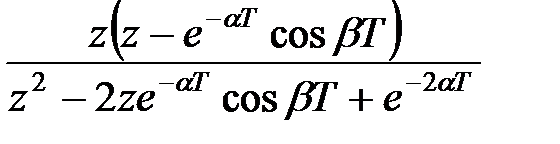
|
Таблиця 19.2. Модифіковані  -зображення
-зображення
| № | 
| 
| 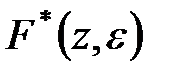
|
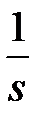
| 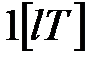
| 
| |
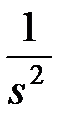
| 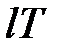
| 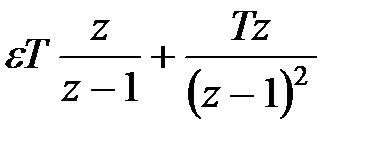
| |
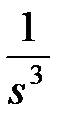
| 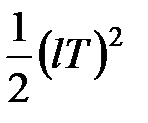
| 
| |
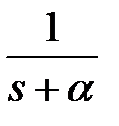
| 
| 
| |

| 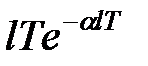
| 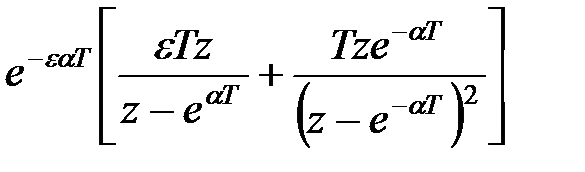
| |
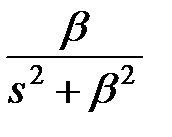
| 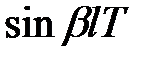
| 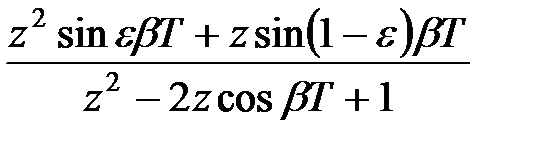
| |
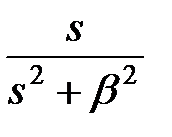
| 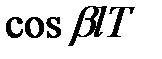
| 
| |
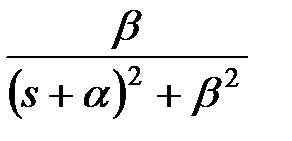
| 
| 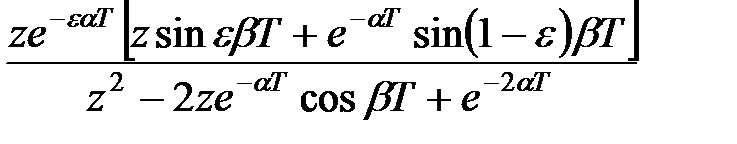
| |
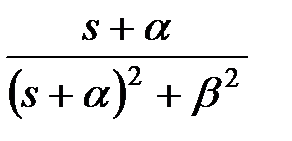
| 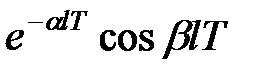
| 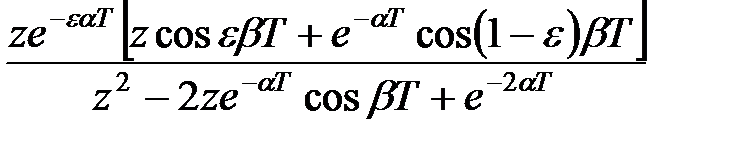
|
1) Модифіковане 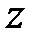 -зображення для одиничної функції
-зображення для одиничної функції 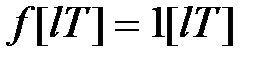 було отримано при розгляді прикладу 19.1 (див. формулу (19.1)).
було отримано при розгляді прикладу 19.1 (див. формулу (19.1)).
2) Модифіковане  -зображення для функції
-зображення для функції 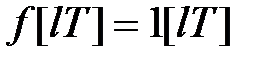 було отримано при розгляді властивості 4°
було отримано при розгляді властивості 4°  -перетворення (див. (19.6)).
-перетворення (див. (19.6)).
3) Для отримання модифікованого  -зображення для функції
-зображення для функції 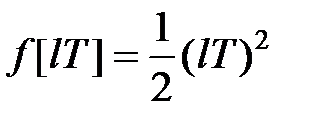 представимо її у вигляді
представимо її у вигляді 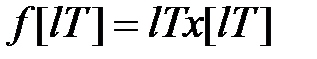 де
де 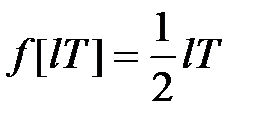 і скористаємося формулою (19.4)
і скористаємося формулою (19.4)
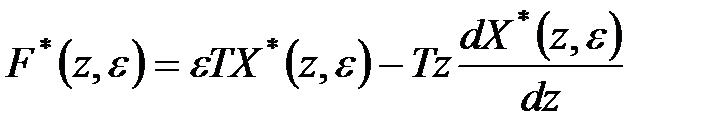
|
Так як
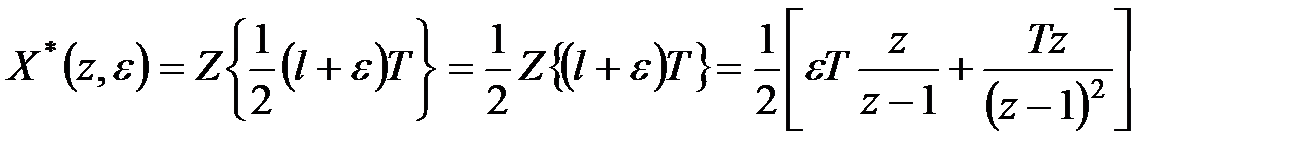
|
то, підставивши цей вираз в приведену вище формулу, отримаємо шуканий вираз для  .
.
4) Модифіковане z-зображення для функції 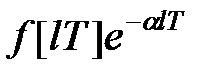 було отримано при розгляді властивості 5°
було отримано при розгляді властивості 5°  -перетворення (див. вираз (19.10)).
-перетворення (див. вираз (19.10)).
5) Для отримання модифікованого  -зображення функції
-зображення функції  представимо її у вигляді
представимо її у вигляді 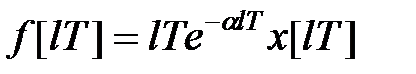 де
де 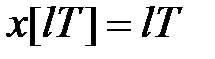 і скористаємося формулою (19.8)
і скористаємося формулою (19.8)
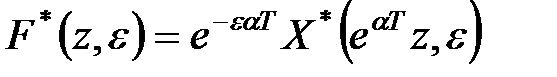 . .
|
Оскільки
 , ,
|
то
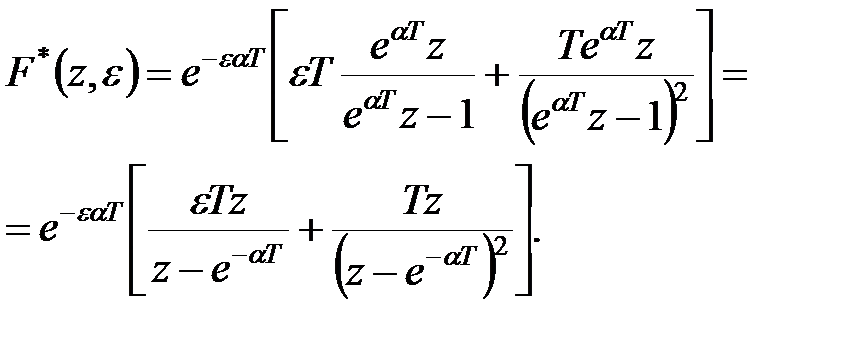
|
При отриманні формул 6-9 з табл. 19.2 використовується модифіковане  -зображення
-зображення 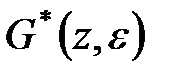 функції
функції  . Для знаходження
. Для знаходження 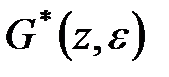 представимо останню функцію у вигляді
представимо останню функцію у вигляді  , де
, де 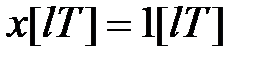 і скористаємося формулою (19.8):
і скористаємося формулою (19.8):
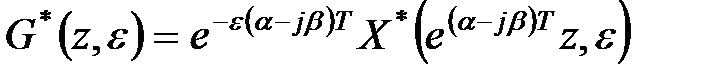 . .
|
Враховуючи, що модифіковане  -зображення одиничної функції має вигляд
-зображення одиничної функції має вигляд
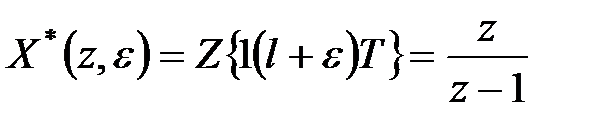 , ,
|
знаходимо
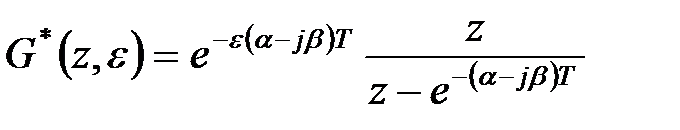 . .
|
Помножимо чисельник і знаменник на комплексно-зв'язане із знаменником число:

|
Використовуючи формулу Ейлера 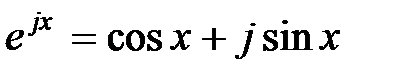 останній вираз можна перетворити до вигляду
останній вираз можна перетворити до вигляду

| (19.16) |
6) Функція 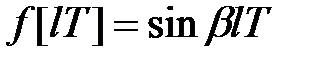 пов'язана з функцією
пов'язана з функцією 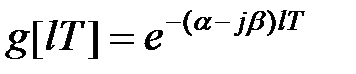 співвідношенням
співвідношенням
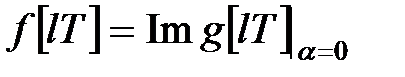 . .
|
Тому (див. (19.16))
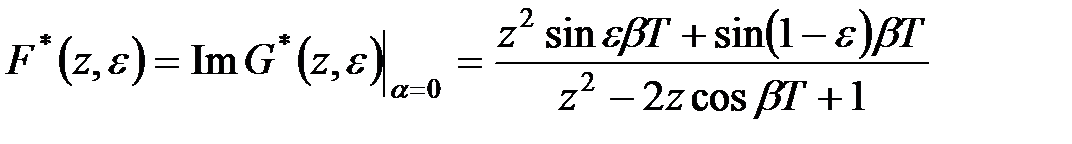 . .
|
7) Функція 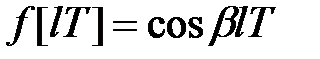 пов'язана з функцією
пов'язана з функцією 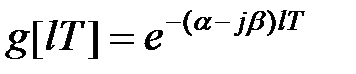 співвідношенням
співвідношенням
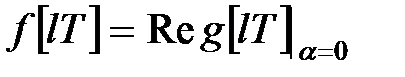 . .
|
Тому
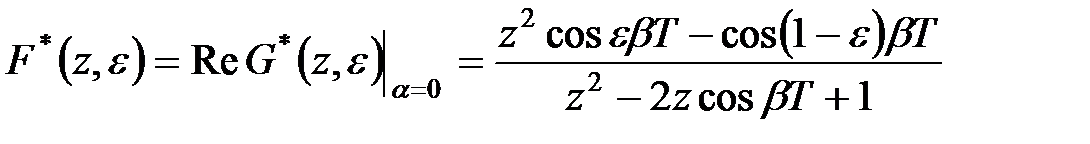 . .
|
8) Функція 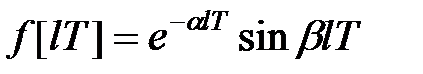 пов'язана з функцією
пов'язана з функцією 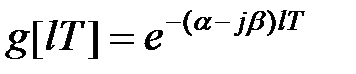 співвідношенням
співвідношенням
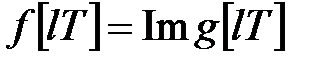 . .
|
Тому (див.(19.16))
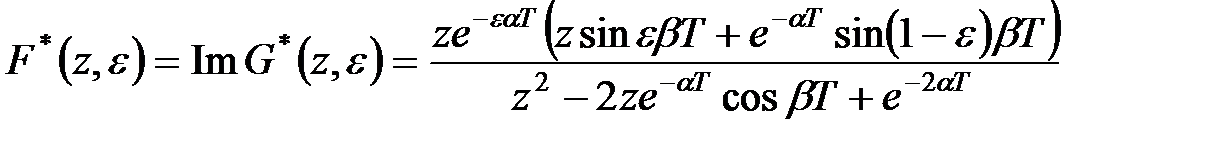
|
9) Функція 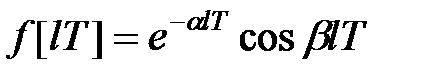 пов'язана з функцією
пов'язана з функцією 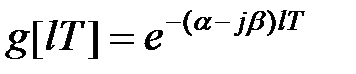 співвідношенням
співвідношенням
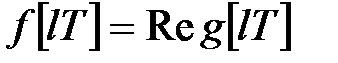 . .
|
Тому
 . .
|
Дата добавления: 2017-08-01; просмотров: 261;
