Основні властивості -перетворення
Оскільки  -перетворення від
-перетворення від 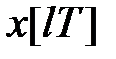 можна розглядати як окремий випадок модифікованого
можна розглядати як окремий випадок модифікованого  -перетворення при
-перетворення при 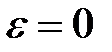 , то розглянемо властивості модифікованого
, то розглянемо властивості модифікованого  -перетворення. Докази приводяться в кінці, після розгляду всіх властивостей.
-перетворення. Докази приводяться в кінці, після розгляду всіх властивостей.
1°. Лінійність. Модифіковане  -перетворення від лінійної комбінації дискретних функцій дорівнює лінійній комбінації їх модифікованих
-перетворення від лінійної комбінації дискретних функцій дорівнює лінійній комбінації їх модифікованих  -перетворень:
-перетворень:
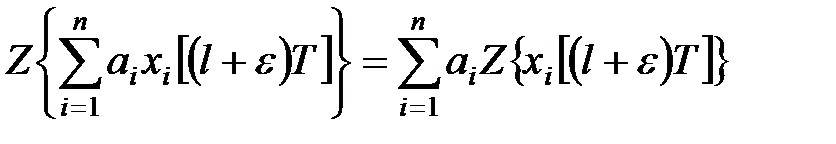 . .
|
Тут 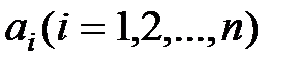 – константи.
– константи.
2°. Теорема запізнювання. Модифіковане  -перетворення від функції з аргументом з запізненням
-перетворення від функції з аргументом з запізненням 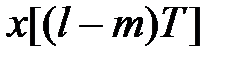 визначається таким чином:
визначається таким чином:
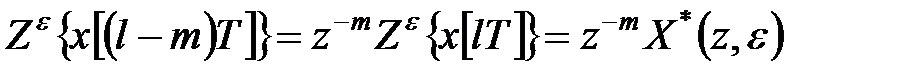 , ,
| (19.2) |
3°. Теорема випередження. Модифіковане  -перетворення від функції з випереджаючим аргументом
-перетворення від функції з випереджаючим аргументом 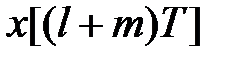 визначається таким чином:
визначається таким чином:
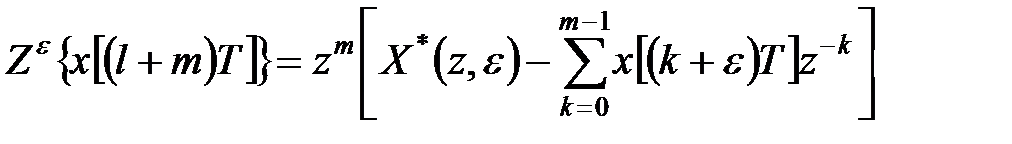 . .
|
Якщо 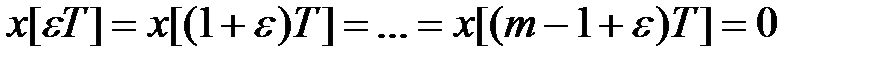 (початкові умови нульові), то
(початкові умови нульові), то
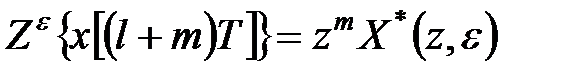 . .
| (19.3) |
4°. Множення оригіналу на 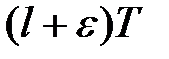 .
.  -перетворення від добутку
-перетворення від добутку 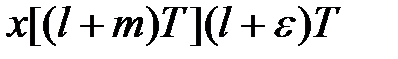 визначається таким чином:
визначається таким чином:
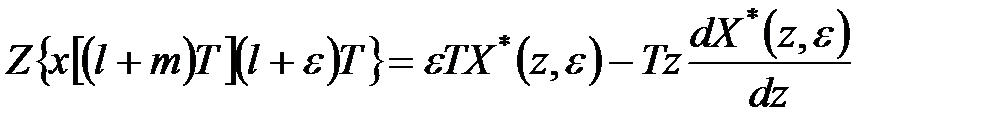 . .
| (19.4) |
При 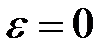 маємо
маємо
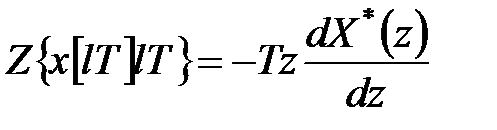 . .
| (19.5) |
Користуючись отриманою властивістю, знайдемо звичайне і модифіковане  -зображення функції
-зображення функції 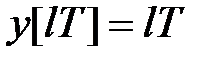 .
.
Модифіковане  -зображення для одиничної функції (19.1) має вигляд
-зображення для одиничної функції (19.1) має вигляд
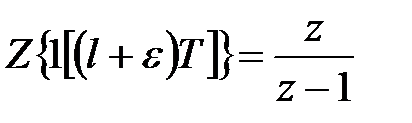 . .
|
Тому якщо в (19.4) припустимо 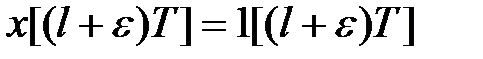 то отримаємо
то отримаємо
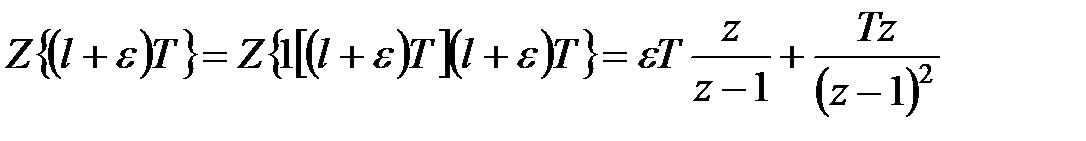
| (19.6) |
Звідси при 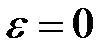 маємо
маємо
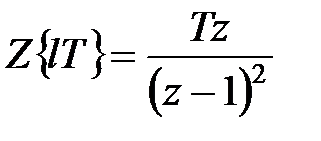
| (19.7) |
5°. Множення оригіналу на 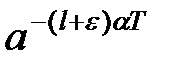 .
.  -перетворення від добутку
-перетворення від добутку 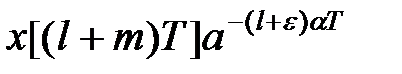 визначається таким чином:
визначається таким чином:
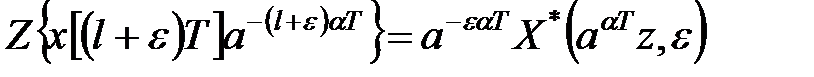 . .
| (19.8) |
При 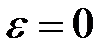 маємо
маємо
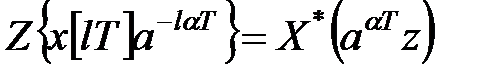 . .
| (19.9) |
Знайдемо звичайне і модифіковане 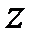 -зображення функції
-зображення функції
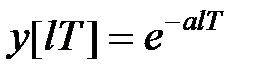 . Прирівнявши в (19.8)
. Прирівнявши в (19.8)
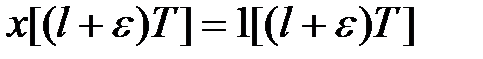 ,
, 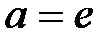
отримаємо
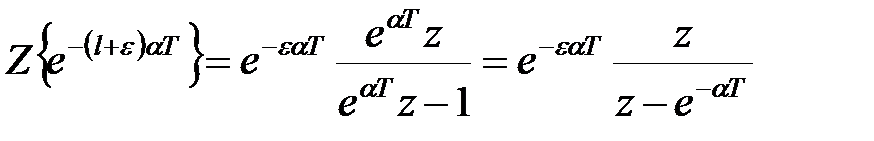 . .
| (19.10) |
При 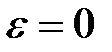 маємо
маємо
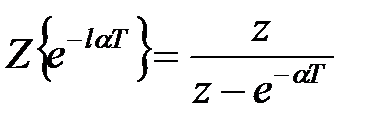 . .
| (19.11) |
6°. Теорема про згортання. Добуток зображень 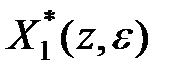 і
і 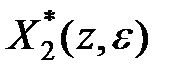 дорівнює
дорівнює 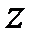 -перетворенню від згортання їх оригіналів
-перетворенню від згортання їх оригіналів 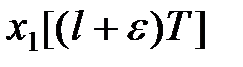 і
і 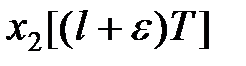 :
:
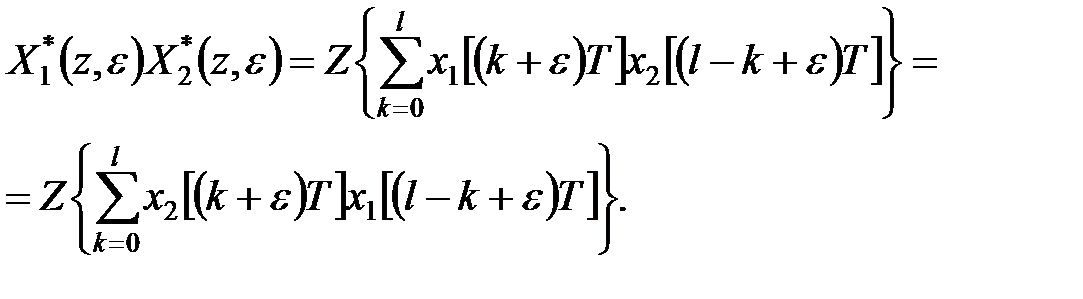
| (19.12) |
При 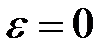 маємо
маємо
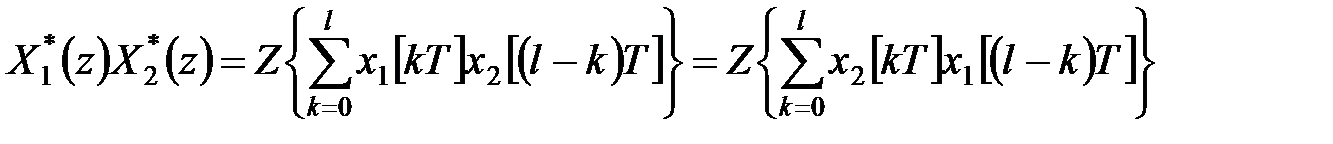 . .
| (19.13) |
7°. Теореми про граничні значення. Початкове значення гратчастої функції 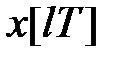 по її звичайному і модифікованому
по її звичайному і модифікованому 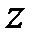 -зображенню визначається таким чином:
-зображенню визначається таким чином:
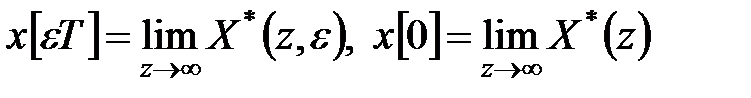 . .
| (19.14) |
Межа 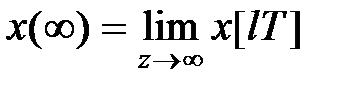 за умови, що вона існує, визначається таким чином:
за умови, що вона існує, визначається таким чином:
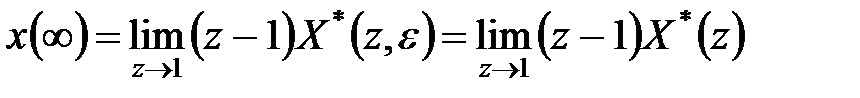
| (19.15) |
Доказ властивостей z-перетворювання
1°. Лінійність. Згідно визначенню модифікованого 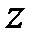 -перетворення
-перетворення
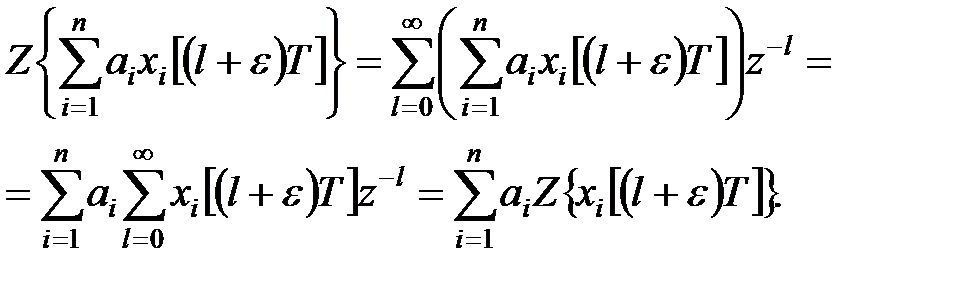
|
2°. Теорема запізнювання. У 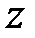 -перетворенні
-перетворенні
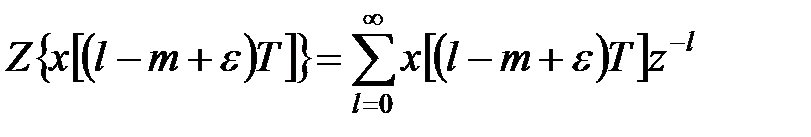 , ,
|
у правій частині зробимо підстановку 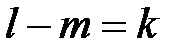 :
:
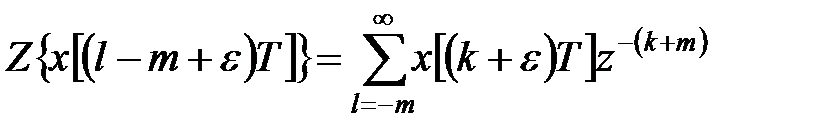 . .
|
Оскільки функція-оригінал дорівнює нулю при від’ємних аргументах, з останньої рівності отримуємо
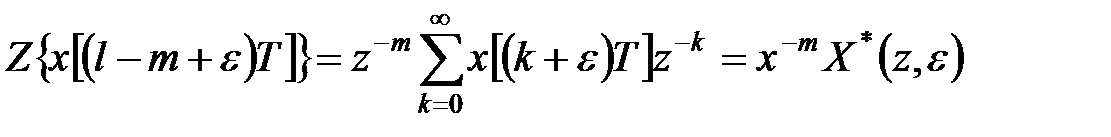 . .
|
3°. Теорема випередження. Ця теорема доводиться так само, як і теорема запізнювання.
4°. Множення оригіналу на 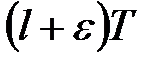 . Продиференціюємо обидві частини
. Продиференціюємо обидві частини 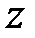 -перетворення
-перетворення
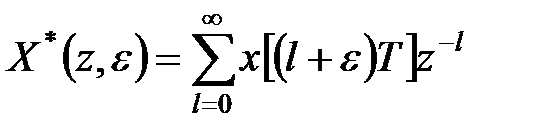 , ,
|
по 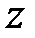 і помножимо на
і помножимо на 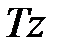 :
:
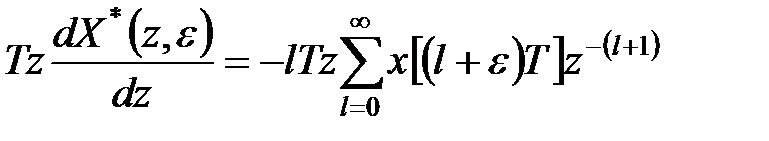 . .
|
Віднімемо цей вираз з попередньої рівності, заздалегідь помноживши його на 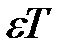 :
:
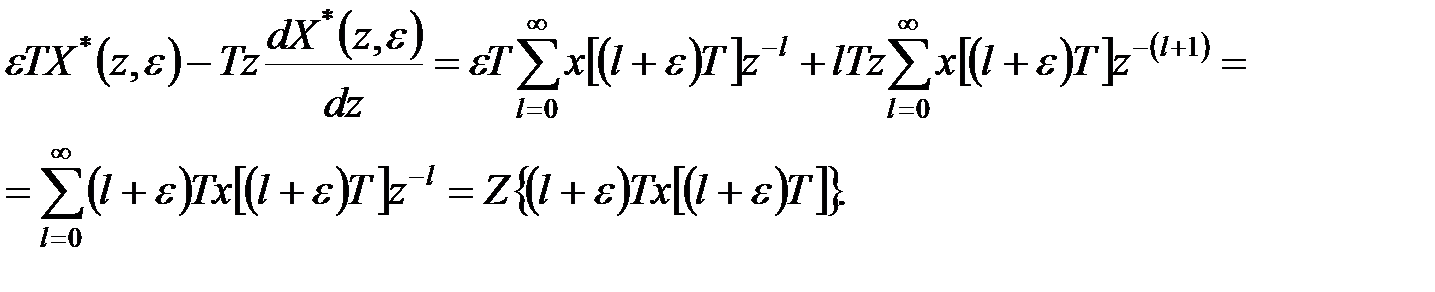
|
5°. Множення оригіналу на 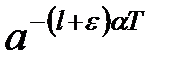 . Згідно визначенню
. Згідно визначенню 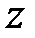 -перетворення
-перетворення
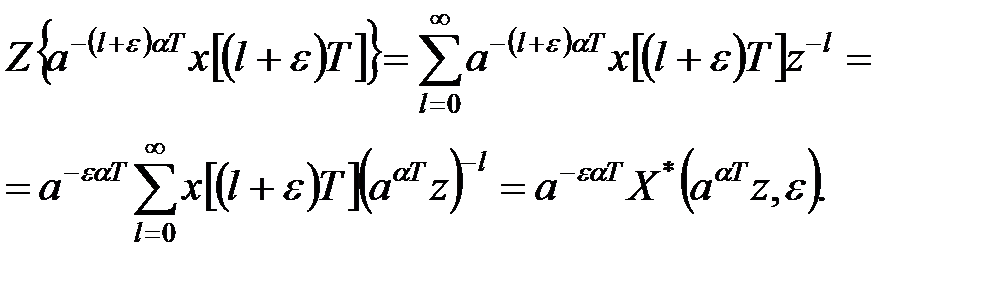
|
6°. Теорема про згортання. Скориставшись визначенням 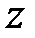 -перетворення, можемо записати
-перетворення, можемо записати
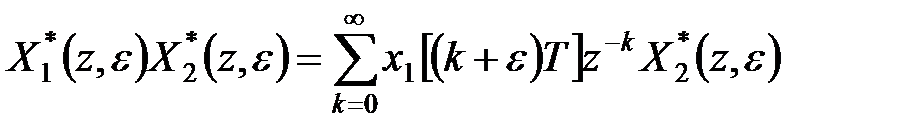 . .
|
За теоремою запізнювання (див. (19.2))
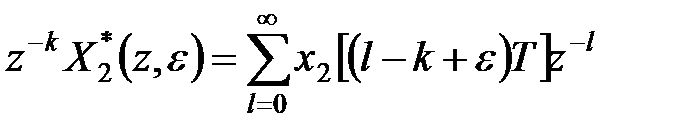 . .
|
Підставивши цей вираз в попередню рівність, знаходимо
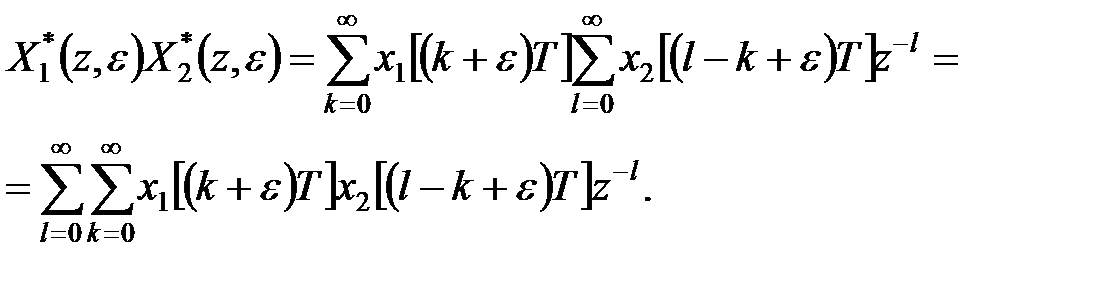
|
Звідси, враховуючи, що 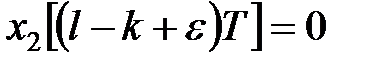 при
при 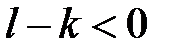 отримуємо
отримуємо
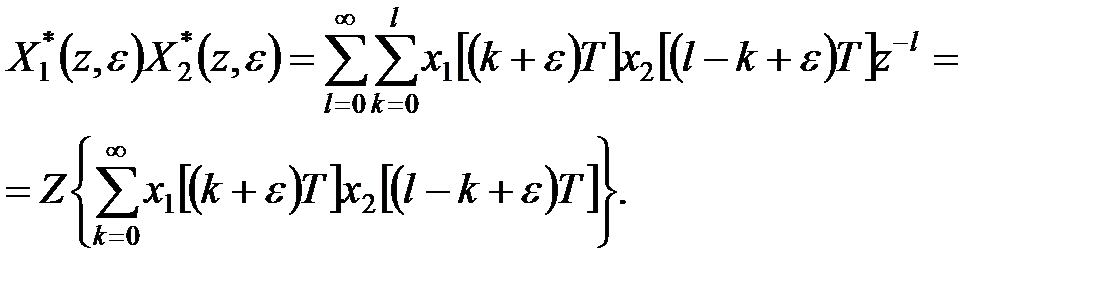
|
Аналогічно, використовуючи рівність
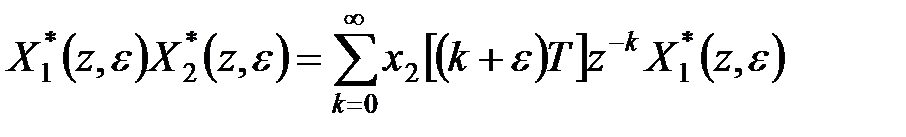 , ,
|
отримаємо
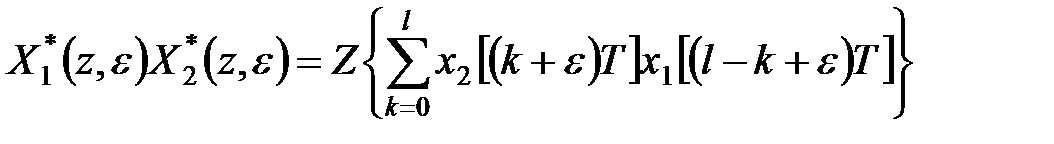 . .
|
7°. Теореми про граничні значення. Представимо 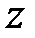 -перетворення від функції
-перетворення від функції 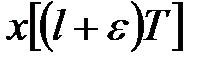 у вигляді
у вигляді
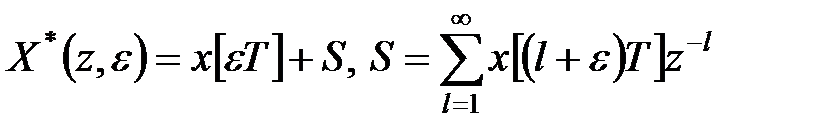 . .
|
За визначенням функції-оригіналу існують додатні числа 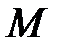 і
і 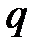 такі, що
такі, що 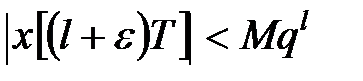 . Тому
. Тому
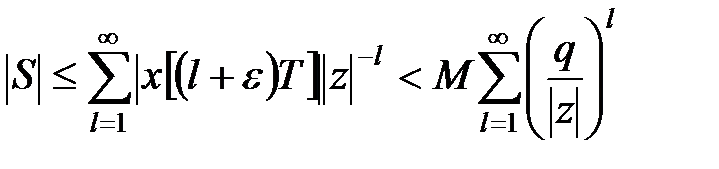 . .
|
При 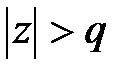 по формулі суми нескінченно убуваючої геометричної прогресії маємо
по формулі суми нескінченно убуваючої геометричної прогресії маємо
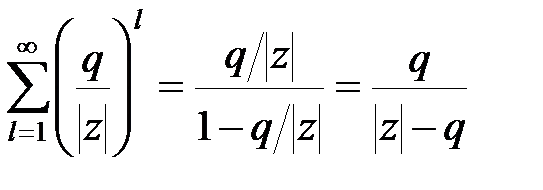 . .
|
І так як
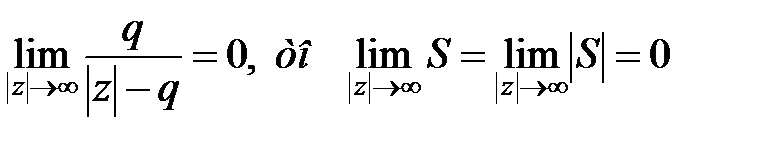 , ,
|
та
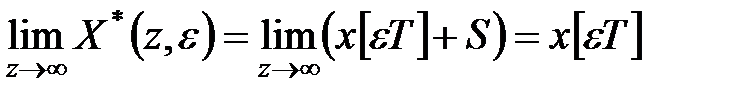 . .
|
Звідси при 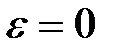 маємо
маємо
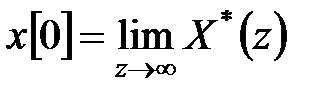 . .
|
Отже, формули (19.14) доведені.
Тепер доведемо формулу (19.15). Використовуючи властивість лінійності 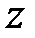 -перетворення і теорему випередження, можемо записати
-перетворення і теорему випередження, можемо записати
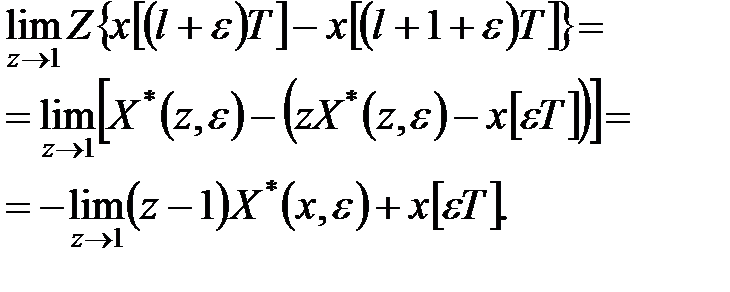
|
Ліву частину верхньої рівності можна також перетворити таким чином:
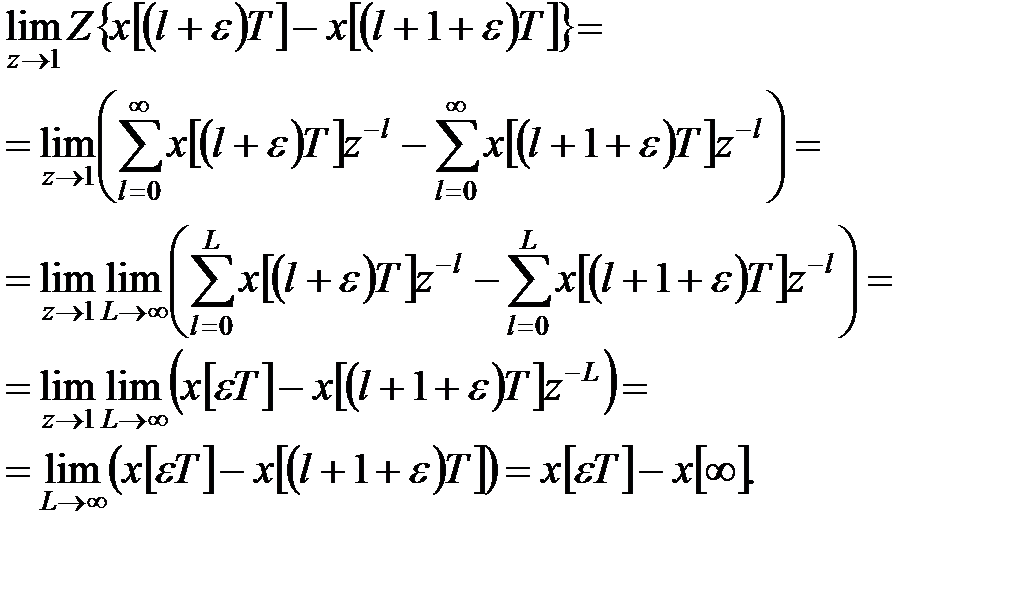
|
Прирівняємо праві частини отриманої рівності:
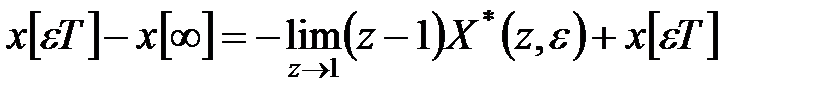 . .
|
Звідси отримуємо
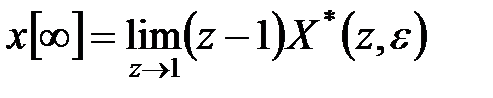 , ,
|
і при 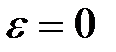
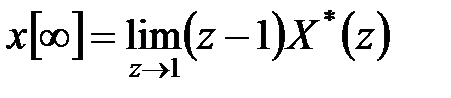 . .
|
Дата добавления: 2017-08-01; просмотров: 296;
