Лінійні різницеві рівняння
Рівняння
 , ,
| (18.4) |
яке отримують з рівняння (18.3) прирівнюванням до нуля правої частини, називається однорідним (кінцевим) різницевим рівнянням, відповідним неоднорідному різницевому рівнянню (18.3).
Використовуючи оператор зсуву  рівняння (18.3) можна записати в операторній (символічній) формі
рівняння (18.3) можна записати в операторній (символічній) формі
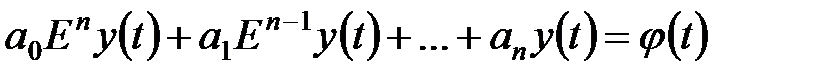 , ,
|
або
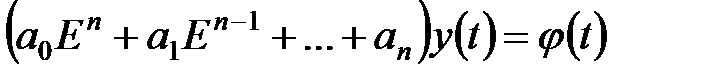 . .
| (18.5) |
Відповідне однорідне рівняння в операторній формі приймає вигляд
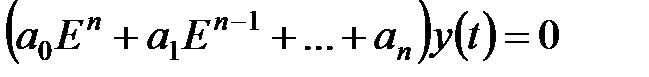 . .
| (18.6) |
Загальне вирішення неоднорідного різницевого рівняння (18.3) має вигляд
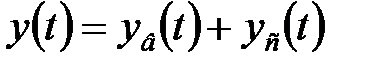 , ,
|
де 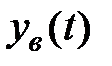 – частинне вирішення цього рівняння, що визначає вимушений рух, і
– частинне вирішення цього рівняння, що визначає вимушений рух, і 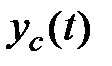 – загальне вирішення відповідного однорідного рівняння, що визначає вільний рух.
– загальне вирішення відповідного однорідного рівняння, що визначає вільний рух.
Вирішення однорідного рівняння шукається у вигляді  . Підставивши цей вираз в (18.4), отримаємо
. Підставивши цей вираз в (18.4), отримаємо
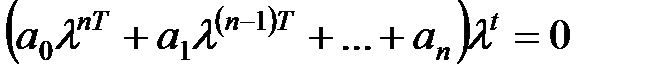 . .
|
Ця рівність буде виконана тотожно відносно  якщо
якщо
 . .
|
Прирівнявши 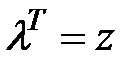 , отримаємо алгебраїчне рівняння
, отримаємо алгебраїчне рівняння
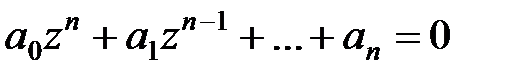 , ,
| (18.7) |
яке називається характеристичним рівнянням. Ліва частина цього рівняння виходить з різницевого оператора при невідомій функції в рівняннях (18.5) і (18.6) при заміні 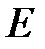 на
на 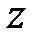 .
.
Таким чином, вирішенням однорідного різницевого рівняння (18.4) буде
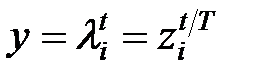 , ,
|
де 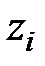 – корінь характеристичного рівняння (18.7).
– корінь характеристичного рівняння (18.7).
Якщо всі корені  характеристичного рівняння прості (тобто різні), то загальне вирішення однорідного різницевого рівняння (18.4) має вигляд
характеристичного рівняння прості (тобто різні), то загальне вирішення однорідного різницевого рівняння (18.4) має вигляд
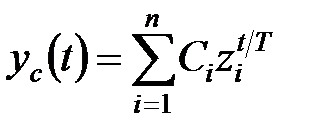 , ,
| (18.8) |
де 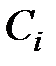 – довільні постійні. Якщо серед коренів характеристичного рівняння є кратний корінь
– довільні постійні. Якщо серед коренів характеристичного рівняння є кратний корінь  кратності
кратності 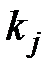 то йому в (18.8) відповідає доданок
то йому в (18.8) відповідає доданок
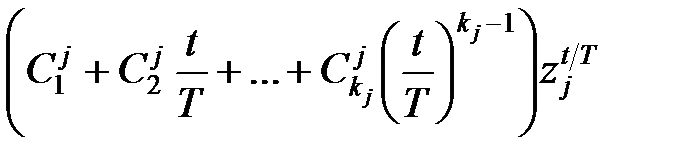 . .
| (18.9) |
Якщо є прості комплексно-зв'язані корені 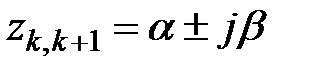 ,то відповідні їм два доданки можна замінити на
,то відповідні їм два доданки можна замінити на
 , ,
|
де  – довільні константи.
– довільні константи.
Приклад 18.1. Знайти загальне вирішення різницевого рівняння
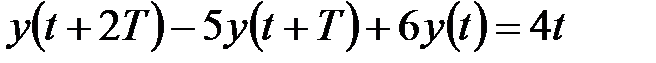 . .
|
Рішення. Частинне рішення шукатимемо у вигляді
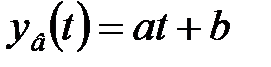 . .
|
Підставивши цей вираз в дане рівняння, отримаємо
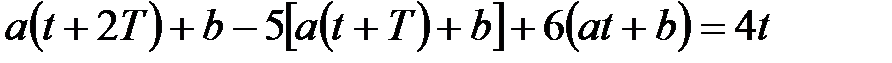 , ,
|
або, після приведення подібних членів
 . .
|
Звідси, прирівнявши коефіцієнти при однакових ступенях  отримуємо
отримуємо
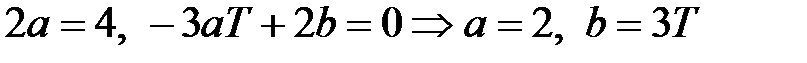 . .
|
Отже, частинне рішення є
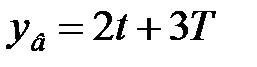 . .
|
Характеристичне рівняння має вигляд
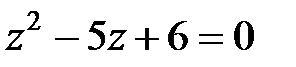 . .
|
Коренями цього рівняння є
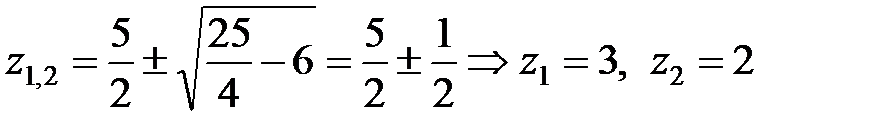
|
Тому загальне вирішення однорідного різницевого рівняння має вигляд
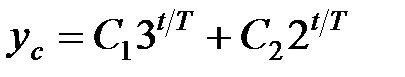 , ,
|
а загальне вирішення неоднорідного різницевого рівняння є
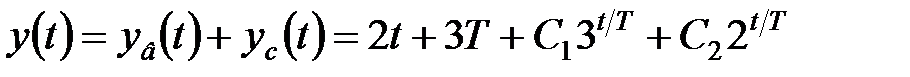 . .
|
Приклад 18.2. Визначити вирішення різницевого рівняння
 , ,
|
за нульових початкових умов 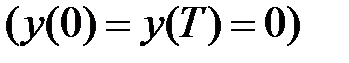 .
.
Рішення. Частинне рішення шукатимемо у вигляді константи 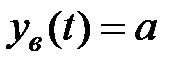 . Підставивши цей вираз в дане рівняння, отримаємо
. Підставивши цей вираз в дане рівняння, отримаємо
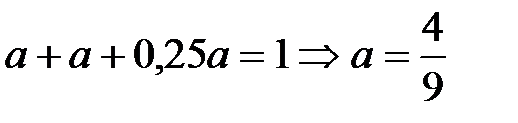 . .
|
Характеристичне рівняння
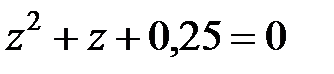 , ,
|
має двократний корінь 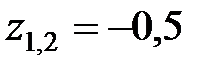 . Загальне вирішення однорідного різницевого рівняння –
. Загальне вирішення однорідного різницевого рівняння –
 , ,
|
і загальне вирішення неоднорідного рівняння –
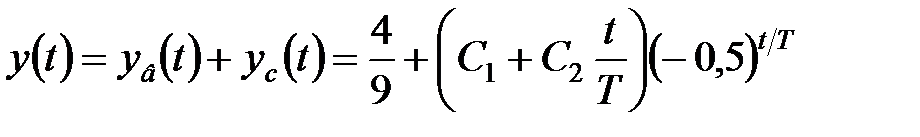 . .
|
З початкових умов маємо
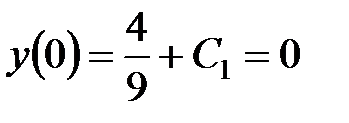 , ,
 . .
|
Вирішивши цю систему рівнянь, отримаємо  .
.
Отже, шукане рішення має вигляд
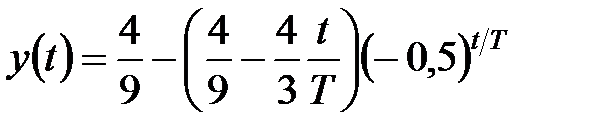 . .
|
Дата добавления: 2017-08-01; просмотров: 250;
