Визначення -перетворення

-перетворенням, або перетворенням Лорана, називається співвідношення

,

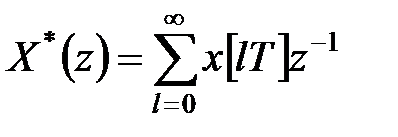(19.1)

що ставить у відповідність дискретній функції 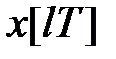функцію комплексного змінного 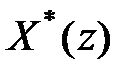При цьому 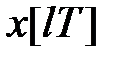називають оригіналом, а 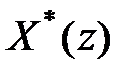– зображенням або -зображенням. Оригінал і його зображення позначають однойменними буквами: оригінал – рядковою буквою, а зображення – прописною буквою із зірочкою -перетворення також умовно записують у вигляді

,

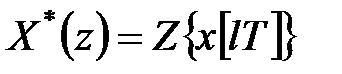а зворотне -перетворення – у вигляді

.

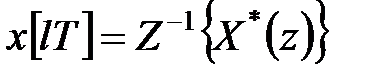Передбачається, що в -перетворенні (19.1) дискретна функція має наступні властивості:

1°) існують додатні числа М і q такі, що 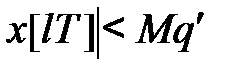при будь-яких ;

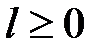2°) 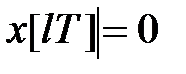при всіх .

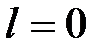Властивість 1°) необхідна для існування області збіжності ряду в правій частині (19.1), а властивість 2°) використовується при виведенні деяких властивостей -перетворення. Функції, що задовольняють вказаним двом властивостям, називають функціями-оригіналами. -перетворення від зміщеної гратчастої функції 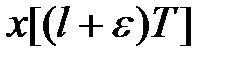тобто співвідношення

,

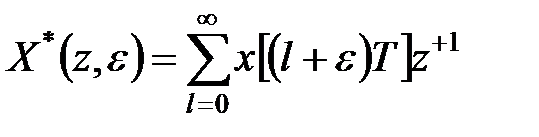називають модифікованим -перетворенням. Модифіковане -перетворення також записують у вигляді

.

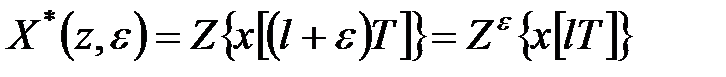Функцію 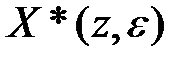називають -зображенням зміщеної гратчастої функції 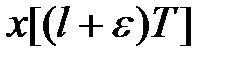або модифікованим -зображенням гратчастої функції .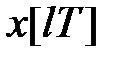

Приклад 19.1. Визначити -зображення одиничної гратчастої функції 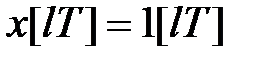і зміщеної гратчастої функції .

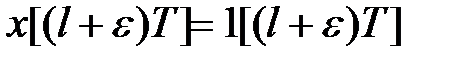Рішення. Оскільки при всіх 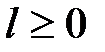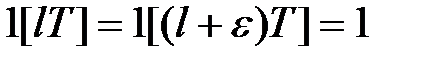то

.

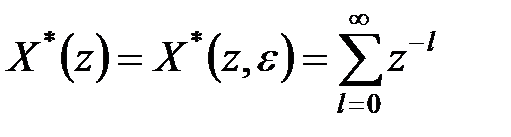По формулі суми нескінченно убуваючої геометричної прогресії маємо

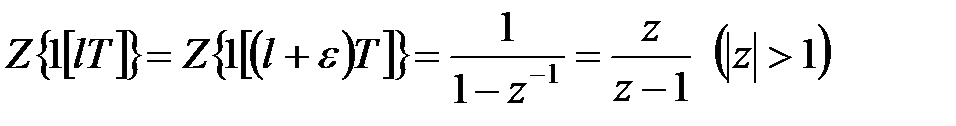
(19.1)