Рівняння і передаточні функції дискретних систем

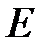Якщо дискретна система задається різницевим рівнянням, то її передаточні функції визначаються аналогічно передаточним функціям безперервних систем. Відмінність полягає тільки в тому, що у разі дискретних систем замість оператора диференціювання використовується оператор зсуву а замість перетворення Лапласа – 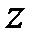-перетворення.

Хай дискретна система управління описується різницевим рівнянням

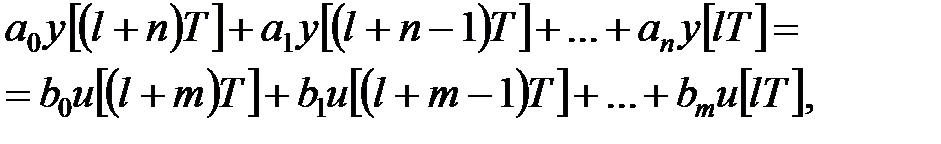
(20.1)

де 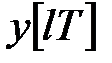– вихідна змінна, 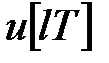– вхідна змінна 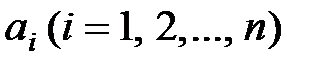і 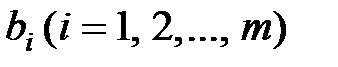– константи. У операторній формі це рівняння приймає вигляд

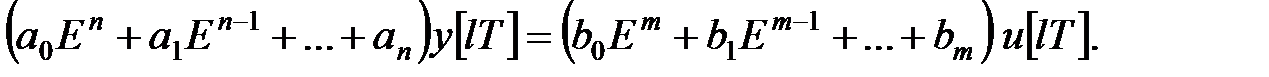
Різницевий оператор при вихідний змінній 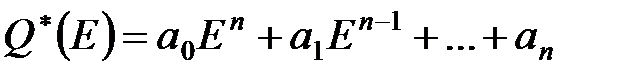називається власним (різницевим) оператором, а різницевий оператор при вхідній змінній 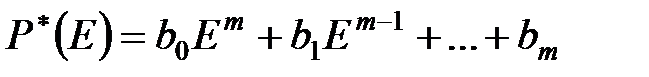– (різницевим) оператором дії.

Відношення оператора дії до власного оператора називається передаточною функцією в операторній формі.

Відповідно до цього визначення передаточна функція (у операторній формі) системи управління (20.1) дорівнює

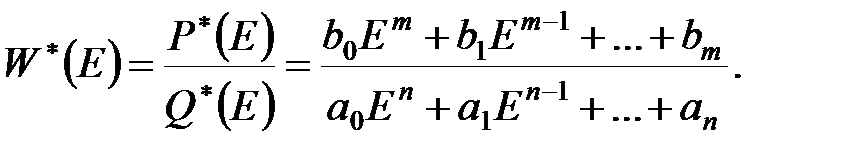
(20.2)

Відношення 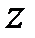-зображень, що має найменший порядок (за нульових початкових умов) вихідної і вхідної змінних називається передаточною функцією в 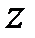-зображеннях.

Для обчислення передаточної функції в 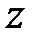-зображеннях системи управління (20.1) застосуємо до обох частин цього рівняння 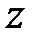-перетворення. Використовуючи властивість лінійності 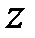-перетворення, можемо записати

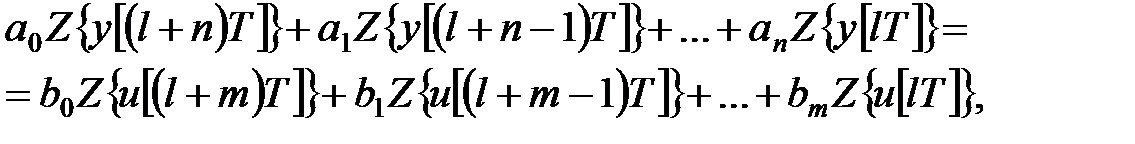
Відповідно до теореми випередження за нульових початкових умов 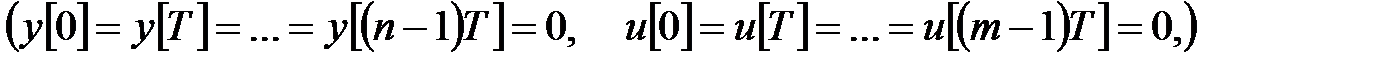маємо

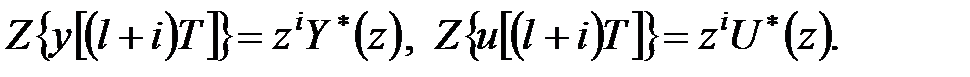
Тому

Звідси для передаточної функції в 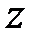-зображеннях отримуємо

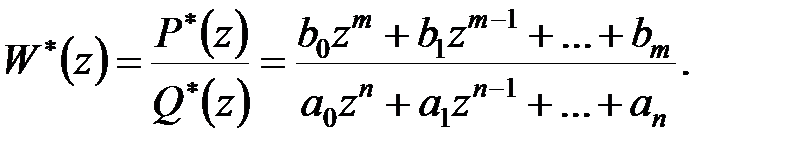
(20.3)

Порівнюючи передаточні функції в операторній формі (20.2) і в 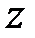-зображеннях, неважко відмітити, що

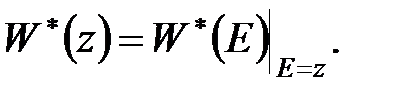
Передаточна функція 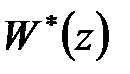є функцією комплексної змінної 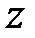і за визначенням вона не містить однакових нулів і полюсів. Тому якщо передаточна функція в операторній формі має однакові нулі і полюси, зворотна рівність не має місця.

Передаточна функція 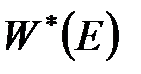є оператором і рівняння

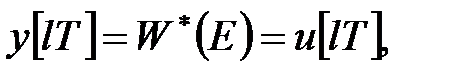
де 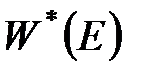визначається співвідношенням (20.2), є операторною (символічну) формою запису рівняння (20.1). У правій частині не можна переставляти місцями оператор і вхідну змінну.

Отже, якщо дискретна система управління задана різницевим рівнянням, то процес обчислення передаточних функцій нічим не відрізняється від процесу обчислення передаточних функцій безперервних систем. Проте, як правило, доводиться обчислювати передаточні функції, коли відомі характеристики дискретних елементів і передаточна функція безперервної частини. І в цьому випадку виникають особливості, які роблять обчислення передаточних функцій дискретних систем складнішим.