ВИЗНАЧЕННЯ НАПРУЖЕНЬ В ГРУНТАХ

В будь-якій точці грунтового масиву виникає система напружень, спричинена власною вагою вищележачих шарів грунту – природні напруження та прикладеного до поверхні грунтового масиву зовнішнього навантаження – додаткові напруження. Дослідженням встановлено: грунт в більшості випадків не є пружним тілом (залишкові деформації в грунті значно більші від пружних – компресійна крива рис. 4.2); грунту не властива строга лінійна залежність між напруженнями і деформаціями (компресійна крива рис. 4.2). Крім того, в більшості випадків грунт є несуцільним (дисперсним) тілом (п. 1.2). В зв‘язку з цим виникає питання, в яких випадках допустимо використовувати рішення теорії пружності, для визначення напружень в грунтах. Для вияснення цього розглянемо переміщення фундамента від дії статичного навантаження.

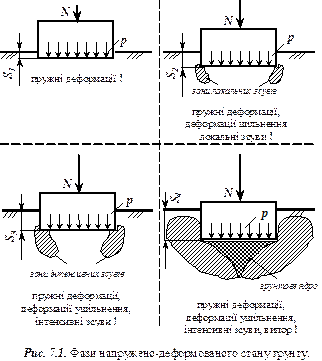
1. Фази напруженого стану грунтів. Нехай на поверхні грунту встановлено жорсткий фундамент (рис. 7.1), завантажений навантаженням 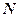. Під дією цього навантаження в масиві грунту відбуваються переміщення, величина яких буде збільшуватись по мірі збільшення тиску (p=N/A) на грунт основи. Графік залежності осідань фундаменту 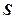від тиску 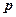під його підошвою має вигляд (рис. 7.2). На кривій можна виділити чотири ділянки. Перша 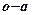відповідає навантаженню, при якому напруження, що виникають в грунті під основною частиною фундамента не перевищують структурну міцність грунту 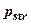. Цю фазу називають фазою пружних деформацій, хоч одночасно з ними під краями фундаменту, де відбувається концентрація напружень, розвиваються пластичні деформації і деформації ущільнення. Остання обставина призводить до того, що в межах цієї фази між осіданням і тиском немає строгої лінійної залежності.

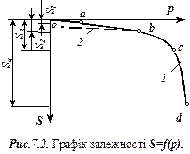При подальшому збільшенні тиску, внаслідок нерівномірності його розподілу по підошві фундаменту напруження під краями будуть перевищувати структурну міцність. Це призведе до перерозподілу тиску. Коли тиск під всією підошвою фундаменту перевищить структурну міцність грунту, в основі стануть розвиватися деформації ущільнення. При тисках, які незначно перевищують структурну міцність грунту, ущільнення розвивається лише в зоні, яка безпосередньо прилягає до підошви фундамента. По мірі збільшення тиску грунт буде ущільнюватись у все більшій зоні, оскільки в межах все більшого об‘єму напруження будуть перевищувати структурну міцність грунту. Одночасно в грунті під краями фундаменту будуть розвиватися деформації зсувів, поглиблюючи криволінійність ділянки 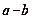. Проте при порівняно незначних тисках (0,1…0,5мПа), які зазвичай виникають під підошвою фундаментів, криву 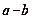можна з деяким наближенням прийняти за пряму. Цю фазу напружено-деформованого стану грунту називають фазою ущільнення. В цій фазі грунт ущільнюється, а його будівельні властивості покращуються (безпосередньо під підошвою фундаменту формується грунтове ядро). Залежність між деформаціями грунту і напруженнями носить приблизно лінійний характер. Для цієї ділянки можна застосувати принцип лінійної деформованості грунтів.

При подальшому збільшенні тиску зони зсувних деформацій поширюючись в сторони, будуть призводити до ущільнення грунту і по сторонах від цих зон, внаслідок чого вигин кривої на ділянці 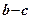стане більшим. Ця ділянка відповідає значному розвитку локальних зсувів, тому цю фазу напружено-деформованого стану грунту в основі фундаменту називають фазою локальних зсувів. Залежність осідань від тиску на цій ділянці нелінійна.

При подальшому збільшенні тиску зони локальних зсувів розширюються і в момент, коли досягають ширини фундаменту, відбувається різке осідання фундаменту. На кривій появляться майже вертикальна крива ділянка 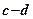, що характеризує цю фазу, яка називається фазою випирання.

Таким чином, четверта фаза абсолютно недопустима для експлуатації будівель і споруд. Вони можуть експлуатуватись в першій і другій фазі (в третій - при умові, що фактичні осідання фундаментів не перевищують їх допустимі значення).

2. Основні припущення. Вище (п. 7.1) було доведена можливість використання в межах двох фаз напружено-деформованого стану (пружних деформацій і локальних зсувів) лінійної залежності між тиском і осіданням фундаменту. Отже, в межах цих фаз грунт вважають лінійно-деформованим тілом.

Внаслідок несуцільності (дисперсності) грунту встановити дійсний напружений стан, який виникає в якій-небудь точці його масиву, з використанням теорії пружності неможливо. Тому обмежуються визначенням середньої інтенсивності напружень в потрібній точці основи, приймаючи умовно, що грунт є суцільним тілом.

Більшість грунтів володіє анізотропією. Проте при рішенні інженерних задач з деяким наближенням приймають, що грунти є ізотропними.

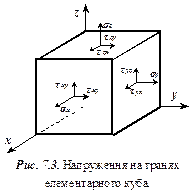Розглянемо, як розвиваються деформації грунту в основі фундамента при його розвантаженні. Для цього будемо розвантажувати фундамент після ущільнення грунту основи тиском, який ще не викликав інтенсивних місцевих зсувів. При зменшенні тиску зменшується осідання (крива 2 рис. 7.2). Після повного зняття тиску крива 2 ніколи не повернеться в початок координат, оскільки грунт отримав залишкові деформації. Отже, грунт не є пружним тілом. Внаслідок цього рішення теорії пружності для ізотропних тіл можна використовувати лише при одноразовому завантаженні основи. Оскільки, основи фундаментів зазнають переважно одноразове завантаження (під час спорудження будівлі), то рішення теорії пружності можуть бути використані при вирішенні розглядуваних задач.

3. Напруження в грунті від дії зосередженого навантаження. Напружений стан у деякій точці простору характеризується сукупністю діючих у ній напружень. В умовах просторової задачі виділяють такі напруження (рис. 7.3).

Задача по визначенню напружень в ідеальному пружному напівпросторі від дії зосередженої сили, прикладеної на його поверхні, розв’язана в 1885 р. французьким вченим Буссінеском. Розглянемо дію вертикальної зосередженої сили 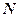, прикладеної в точці 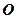до горизонтальної площини, яка є поверхнею лінійно-деформованого напівпростору (рис. 7.4). Від дії сили 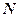у всіх точках напівпростору виникне складний напружено-деформований стан. В загальному випадку в будь-якій точці 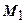напівпростору, дещо віддаленій від точки 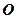, буде діяти шість складових напружень (рис. 7.4. - показано три). Нехай положення точки 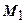(рис. 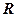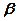7.5) визначається полярними координатами і системи координат з початком в точці прикладання сили 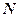. Під дією сили 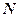точка 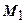переміститься в напрямку радіуса на величину 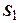. Чим далі від місця прикладення сили 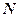буде 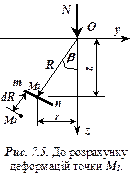розміщена точка 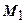, тим меншим буде її переміщення. При 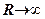переміщення точки 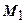буде дорівнювати нулю. Отже, 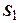можна прийняти обернено пропорційним 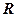. Одночасно при одному й тому ж значенні 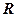для різних величин кута 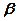переміщення точок будуть неоднакові. Найбільше переміщення отримає точка на осі 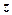, тобто при 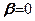. Із збільшенням кута 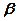переміщення в напрямку радіуса зменшуються і у випадку 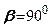(на поверхні грунту) при малих деформаціях будуть рівними нулю. В зв'язку з цим можна прийняти, що переміщення точки 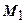у напрямку радіуса (окрім зони біля точки прикладення сили 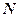) буде

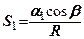, де (7.1)

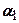- коефіцієнт пропорційності.

Розглянемо зараз точку 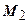, розміщену на продовженні радіуса 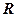на відстані 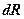від точки 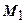. Керуючись записаним виразом (7.1), переміщення точки 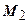у напрямку радіуса 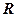становитиме

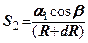(7.2)

Відносна деформація грунту на відрізку 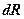буде

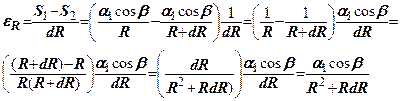(7.3)

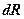Нехтуючи величиною (незрівнянно малою у порівнянні з 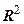) маємо

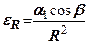(7.4)

Згідно з законом Гука, залежність між напруженнями і деформаціями має вигляд 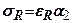( 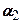- коефіцієнт пропорційності між напруженнями і деформаціями). Підставивши сюда вираз (7.3) знайдемо залежність для напружень стиснення 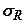, які діють на ділянки, перпендикулярні напрямку радіуса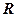

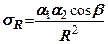(7.5)

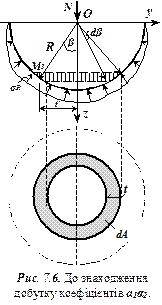
Для знаходження добутку коефіцієнтів 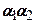виріжемо умовно частину напівпростору напів-шаровою поверхнею (рис. 7.6), яка має центр в точці 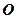і радіус 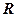, і складемо рівняння рівноваги проекцій на вісь 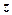всіх сил, які діють на вирізаний елемент. Отримаємо

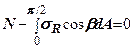, де (7.6)

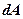- площа кільця напівшарової поверхні при зміні кута 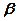на величину : .

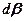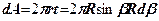Підставляємо в рівняння (7.6) значення для 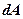і 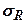з (7.5) одержимо

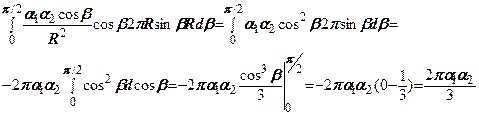
Підставляємо отримане значення у вираз (7.6)

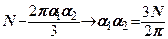
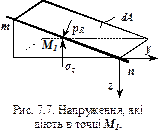Підставивши значення 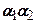у (7.5) отримаємо

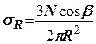(7.7)

На похилу ділянку 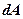діє тиск 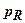(рівний по величині 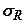, але протилежний йому за напрямом) і напруження 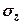, яке нам потрібно знайти. Розглядаючи рівновагу елементарної трикутної призми (рис. 7.7), складемо рівняння проекцій всіх сил на вертикальну вісь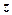

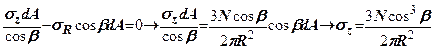(7.8)

Перейдемо до декартової системи координат. Оскільки 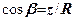(рис. 7.5), то

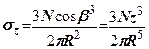(7.9)

Врахувавши те, що 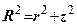і підставляємо його у вираз (7.9), матимемо

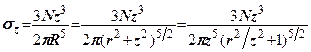(7.10)

Позначимо 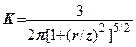- табличний коефіцієнт, тоді

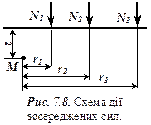
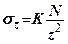(7.11)

Аналогічним чином можуть бути знайдені решта напружень .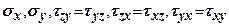

Якщо на поверхні діє декілька сил (рис.7.8), то

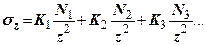(7.12)

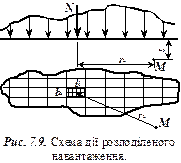4. Напруження в грунті від дії розподіленого навантаження. Нехай до поверхні лінійно-деформованого напівпростору в мажах площі 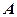прикладено розподілене навантаження змінної в плані інтенсивності (рис. 7.9). Завантажену площу можна розбити на невеличкі прямокутники із сторонами 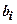, 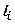і більш складні фігури в межах контуру площі 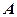. З деяким наближенням тиск, який розподілено в межах і-го прямокутника можна замінити рівнодіючою 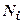, прикладеною в центрі ваги цього тиску. Вертикальне стискуюче напруження 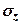в будь-якій точці напівпростору від зосередженої сили можна знайти по аналогії з виразом (7.11)

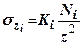
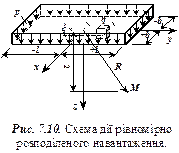Визначивши величину 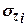від навантаження кожної з елементарних фігур, на які розбита площа 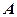і провівши сумування цих напружень, визначимо сумарне напруження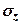

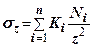(7.13)

5. Напруження в грунті від дії рівномірно розподіленого навантаження. Теоретичне рішення цієї задачі доволі складне. Його отримав А.Ляв в 1929р. Для визначення напружень від дії таких навантажень необхідно розподілити зосереджене навантаження по площі його передачі (проінтегрувати вирази для зосередженої сили по площі її передачі)

Нехай на площі шириною 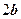і довжиною 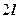діє навантаження інтенсивністю 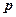(рис. 7.10). Навантаження від елементарної ділянки, яка розміщена на відстані 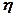i 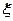від початку координат і має розміри сторін 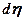i 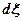замінимо дією елементарної зосередженої сили 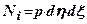. Координата 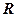точки 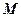, розміщеної на глибині 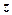становить 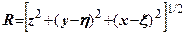. Для інтегрування використаємо вираз (7.9)

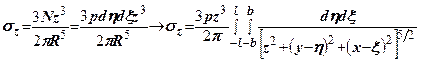(7.14)

Найпростіший результат інтегрування для напружень під кутом фундаменту 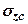має такий вигляд

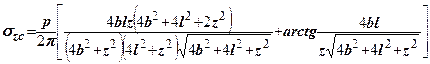(7.15)

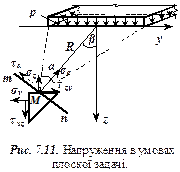Для зручності подібні вирази перетворені до такого виду:

під центром фундаменту

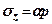(7.16)

під кутом фундаменту

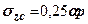, де (7.17)

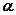- коефіцієнт, який приймається з табл. 1 дод. 2 СНиП 2.02.01-83 залежно від форми підошви фундаменту, співвідношення сторін прямокутного фундаменту і відносної глибини 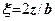- для визначення 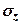, 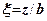- для визначення 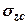; 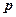- інтенсивність рівномірно розподіленого навантаження; 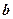- ширина прямокутної площі завантаження; 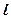- її довжина.

6. Напруження в грунті від дії розподіленого навантаження по смузі. У попередньому пункті (п. 7.5) ми розглянули задачу, коли напруження змінюються у всіх трьох напрямках осей координат. Якщо навантаження розподілене по нескінченній смузі і величина його вздовж смуги не змінюється (рис. 7.11), то для оцінки напружено-деформованого стану масиву достатньо дослідити розподіл напружень у будь-якому поперечному перерізі масиву. Така задача має назву "плоскої". Щодо практичних випадків, то будь-яка задача може бути розглянута як плоска, якщо довжина фундаменту в 10 разів і більше перевищує його ширину.

Вирази для складових напружень при дії рівномірно розподіленого навантаження мають вигляд

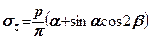(7.18)

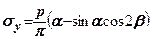(7.19)

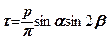, де (7.20)

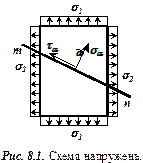
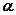- кут зору (рис. 7.11).

З (7.20) видно, що дотичні напруження відсутні, коли кут 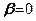, тобто коли нормаль ділянки 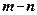співпадає з бісектрисою кута зору (під центром фундаменту). На цих ділянках діють більші головні напруження 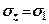, на перпендикулярних - менші 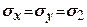(рис. 7.11). Ці напруження визначають за формулами

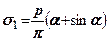(7.21)

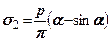(7.22)

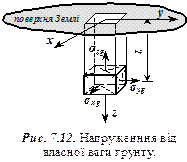7. Напруження в грунті від його власної ваги (природні). На деякій глибині 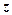від поверхні нормальні напруження 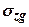від власної ваги грунту на ділянках, паралельних поверхні грунту, становитимуть (рис. 7.12)

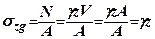, де

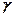- питома вага грунту; 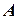- площа поперечного перерізу виділеної призми.

В тому випадку, коли питома вага змінюється з глибиною, товщу грунту 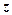ділять на окремі шари товщиною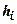

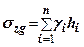, де (7.23)

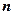- число шарів грунту; 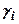, 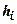- питома вага і товщина кожного шару: .

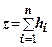Нормальні бічні напруження 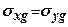(бічний тиск грунту у стані спокою) визначають за формулою

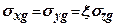, де (7.24)

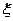- коефіцієнт бічного тиску грунту.

У шарах, розташованих нижче рівня грунтових вод, питома вага всіх водопроникних грунтів приймається з урахуванням зважуючої дії води

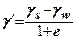, де (7.25)

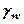- питома вага води.

При наявності водонепроникного шару (глина, важкі суглинки) на рівні його поверхні епюра матиме горизонтальну ділянку, яка дорівнюватиме

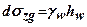, де (7.26)

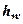- товщина шару води.

8. Розподіл тиску під підошвою фундаментів. Знання закономірностей розподілу напружень під підошвою фундаментів (контактних напружень) необхідне для розрахунків цих конструкцій. Якщо відомий розподіл "контакних напружень" по підошві фундаменту, то без особливих зусиль можна знайти величину розрахункових згинальних моментів і поперечних сил в тілі фундаменту за допомогою звичайних рівнянь статики. Величина "контакних напружень» суттєво залежить від жорсткості фундаменту. Наведені вище залежності будуть справедливі для визначення напружень у масиві грунту, починаючи з деякої, незначної, глибини нижче підошви фундамента. Ці залежності одержані з умови, що навантаження на грунт передається через гнучкий фундамент, тобто деформації цього фундаменту слідують за деформаціями грунту. Реальні фундаменти мають різний струпінь жорсткості. Тому одержані формули непридатні для визначення напружень безпосередньо під підошвою фундаменту.

Із сказаного випливає, що задача визначення контактних напружень не є окремою задачею, а входить до складу загальної задачі визначення напружень у грунтах при різній жорсткості фундаменту (споруди). Тобто розв’язок задачі може бути одержаний на основі вивчення напружено-деформованого стану системи “фундамент-основа”, або, точніше, - системи “споруда-фундамент-основа”. В результаті одержують загальну картину напружень у цих системах, серед яких можуть бути виділені контактні напруження.

Розглянемо якісну картину розподілу контактного тиску під фундаментами різної жорсткості (рис. 7.13). Якщо фундамент абсолютно гнучкий, то найбільші вертикальні напруження виникають під центром завантаженої площадки, внаслідок чого поверхня грунту отримує найбільші осідання в центрі, а найменші в кутових точках. В абсолютно жорсткому фундаменті навпаки концентра-ція напружень відбувається під краями (фази напружено-деформованого стану грунту п. 7.1). Із збільшенням тиску їх величина незрівнянно зростає. Проте такого тиску грунти сприймати не можуть і, внаслідок його перерозподілу, фактична епюра контактних напружень має сідлоподібний вигляд (рис. 7.13).

Виходячи з практичного досвіду і численних експериментальних досліджень епюри в більшості випадків приймають лінійними рис. 7.14

для центрально завантаженого фундаменту

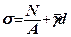(7.27)

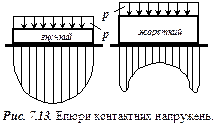
для позацентрово завантаженого фундаменту

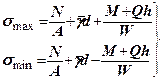, де (7.28)

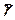- усереднена питома вага фундаменту і грунту на його обрізах.

9. Визначення напружень методом кутових точок. Для визначення стискуючих напружень 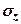в будь-якій точці грунтового масиву під фундаментом або за його межами використовують метод кутових точок. Суть методу полягає в тому, що вантажну площу розділяють на окремі допоміжні прямокутники таким чином, щоб точка, в якій визначається напруження, стала кутовою. Напруження в точці буде дорівнювати алгебраїчній сумі напружень від прямокутників, для яких ця точка буде кутовою. Для пояснення сказаного розглянемо випадки:

точка розміщена під стороною фундаменту (рис. 7.15,а)

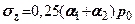(7.29)

точка розміщена під фундаментом (рис. 7.15,б)

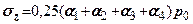(7.30)

Точка розміщена за межами фундаменту (рис. 7.15,в)

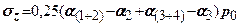, де (7.31)

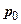- тиск від зовнішнього навантаження на рівні підошви фундамента.