НЕСУЧА ЗДАТНІСТЬ ГРУНТІВ

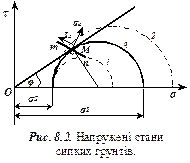1. Гранична напружена рівновага грунту в точці. Гранична напружена рівновага відповідає такому випадку, коли найменше збільшення навантаження викликає втрату стійкості, тобто переміщення одної частини грунту відносно іншої.

Розглянемо умови граничної рівноваги грунту в точці масиву. Для цього в умовах плоскої задачі виділимо деякий елемент у вигляді прямокутника таким чином, щоб на його гранях діяли головні напруження (рис. 8.1).

На ділянці т-п, нормаль якої відхилена на кут α від напрямку дії більшого головного напруження 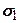, будуть діяти нормальні 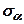і дотичні 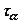напруження. Виразимо їх за допомогою кола Мора (на осі абсцис відкладаємо величини головних напружень 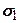і і 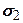будуємо коло діаметром рівним різниці між ними).

Координати будь-якої точки 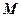, яка знаходиться на колі (рис. 8.2), є величинами нормальних 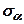і дотичних 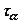напружень, які діють на ділянках, нормаль яких відхилена на кут α від напрямку дії 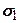. Залежно від орієнтації ділянки 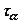змінюється від 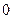до 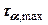. Відповідно нормальні напруження змінюються від 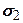до .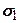

Визначимо умову, при якій у будь-якій точці грунту буде мати місце граничний стан. Розглянемо спочатку сипкий грунт. Залежність між граничними дотичними і нормальними напруженнями для них має вигляд рис. 8.2.

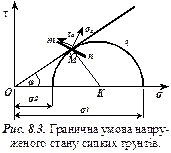Припустимо, що в деякій точці грунту діють такі напруження, що коло Мора розміщене нижче прямої 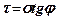(коло 1 рис. 8.2). У цій точці грунт буде мати дограничний стан (зсуву не буде), тому що дотичні напруження на всій сукупності ділянок будуть меншими за граничні дотичні напруження. Якщо коло Мора буде перетинати пряму, то в даній точці (коло 2) грунт буде знаходитись в надграничному стані, тобто зсув уже відбувся (діючі дотичні напруження перевищують граничні). Граничний стан буде мати місце в тому випадку, коли коло і пряма будуть мати одну спільну точку (коло 3).

Отже, у деякій точці може бути таке співвідношення напружень 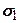і 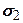, при якому грунт знаходиться в граничному стані. Графічні умови граничного стану для сипких і зв’язних грунтів наведено на рис. 8.3 і рис. 8.4 відповідно.