Закон Био — Савара — Лапласа и его применение к расчету магнитного поля
Магнитное поле постоянных токов различной формы изучалось французскими учеными Ж. Био (1774—1862) и Ф. Саваром (1791—1841). Результаты этих опытов были обобщены выдающимся французским математиком и физиком П. Лапласом.
Закон Био — Савара — Лапласа для проводника с током I, элемент которого dl создает в некоторой точке А (рис. 164) индукцию воля dВ, записывается в вид
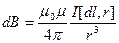,(110.1)
где dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r — радиус-вектор, проведенный из элемента dl проводника в точку А поля, r — модуль радиуса-вектора r. Направление dВ перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление dВ, если поступательное движение винта соответствует направлению тока в элементе.
Модуль вектора dВ определяется выражением
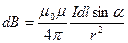,(110.2)
где a — угол между векторами dl и r.
Для магнитного поля,как и для электрического, справедливпринцип суперпозиции:магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторнойсумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:
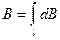
(110.3)
Расчет характеристик магнитного поля (В и H) по приведенным формулам в общем случае сложен. Однако если распределение тока имеет определенную симметрию, то применение закона Био — Савара — Лапласа совместно с принципом суперпозиции позволяет довольно просто рассчитать конкретные поля. Рассмотрим два примера.
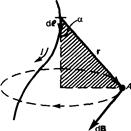
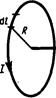
1. Магнитное поле прямого тока — тока, текущего по тонкому прямому провод бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника
|
|
Рис. 164Рис. 165
на расстояние R, векторы dВ от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа (“к нам”). Поэтому сложение векторов dВ можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол a(угол между векторами dl и г), выразив через него все остальные величины. Из рис. 165 следует, что
, 
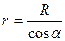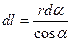
(радиус дуги СD вследствие малости dl равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что магнитная индукция, создаваемая одним элементом проводника, равна
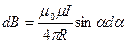(110.4)
Таккак угол a для всех элементов прямого тока изменяется в пределах от 0 до p, то, согласно (110.3) и (110.4),
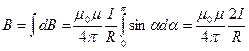
Следовательно, магнитная индукция поля прямого тока
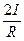(110.5)
2. Магнитное поле в центрекругового проводника с током (рис. 166). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления — вдоль нормали от витка. Поэтому сложение векторовdВ можно заменить сложениемих модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sina=1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2),
.
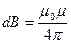
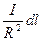Тогда
.
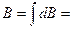
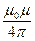
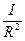
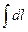
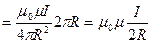Следовательно, магнитная индукция поля в центре кругового проводника с током
.
|
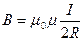§ 111. Закон Ампера. Взаимодействие параллельных токов
Магнитное поле (см. § 109) оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы. Обобщая результаты исследования действия магнитного поля на различные проводники с током, Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, находящегося в магнитном поле,прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длиной dl проводника на магнитную индукцию В:
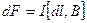(111.1)
Направление вектора dF может быть найдено, согласно (111.1), по общим правилам векторного произведения, откуда следуетправило левойруки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.
Модуль силы Ампера (см. (111.1)) вычисляется по формуле
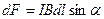,(111.2)
где a — угол между векторамиdI и В.
Закон Ампера применяется для определения силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I1 и I2; (направления токов указаны на рис. 167), расстояние между которыми равно R. Каждый из проводников создает магнитное поле, которое действует по закону Ампера на другой проводник с током. Рассмотрим, с какой силой действует магнитное поле тока I1 на элемент dl второго проводника с током I2. Ток I1 создает вокруг себя магнитное поле, линии магнитной индукции которого представляют собой концентрические окружности. Направление вектора B1 задается правилом правого винта, его модуль по формуле (110.5) равен
.
Направление силы dF1, с которой полеВ1 действует на участок dl второго тока, определяется по правилу левой руки и указано на рисунке. Модуль силы, согласно (111.2), с учетом того, что угол a. между элементами тока I2 и вектором В1 прямой, равен
, 
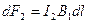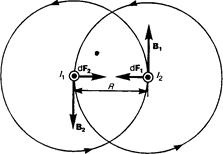
Рис. 167
или, подставляя значение для В1, получим
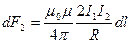(111.3)
Рассуждая аналогично, можно показать, что сила dF1 с которой магнитное поле тока I2 действует на элемент dl первого проводника с током I1, направлена в противоположную сторону и по модулю равна
.(111.4)
Сравнение выражений (111.3) и (111.4) показывает, что
,
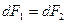т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой
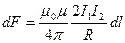(111.5)
Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяемая формулой (111.5).
§ 112. Магнитная постоянная. Единицы магнитной индукции и напряженности магнитного поля
Если два параллельных проводника с током находятся в вакууме (m=1), то сила взаимодействия на единицу длины проводника, согласно (111.5), равна
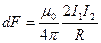(112.1)
Для нахождения числового значения m0 воспользуемся определением ампера, согласно которому при I1=I2=1A и R=1 м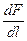 
=2·10-7 Н/м. Подставив это значение в формулу (112.1), получим m0=4p·10-7 Н/А2=4p·10-7 Гн/м, где генри (Гн) — единица индуктивности (см. § 126).
Закон Ампера позволяет определить единицу магнитной индукции В. Предположим, что элемент проводника dl с током I перпендикулярен направлению магнитного поля. Тогда закон Ампера (см. (111.2)) запишется в виде
,
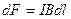откуда
.
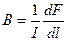Единица магнитной индукции — тесла (Тл): 1 Тл — магнитная индукция такого однородного магнитного поля, которое действует с силой 1 Н на каждый метр длины
прямолинейного проводника, расположенного перпендикулярно направлению поля, если по этому проводнику проходит ток 1 А:
1 Тл==1 Н/(А·м).
Таккак m0=4·10-7 Н/А2, а в случае вакуума (m=1), согласно (109.3), В=m0Н, то для данного случая
.
Единица напряженности магнитного поля —ампер наметр (А/м): 1 А/м — напряженность такого поля, магнитная индукция которого в вакууме равна 4p·10-7 Тл.
§ 113. Магнитное поле движущегося заряда
Каждый проводник с током создает в окружающем пространстве магнитное поле. Электрический же ток представляет собой упорядоченное движение электрических зарядов. Поэтому можно сказать, что любой движущийся в вакууме или среде заряд создает вокруг себя магнитное поле. В результате обобщения опытных данных был установлен закон, определяющий поле В точечного заряда Q, свободно движущегося с нерелятивистской скоростью v. Под свободным движением заряда понимается его движение с постоянной скоростью. Этот закон выражается формулой
,(113.1)
где r — радиус-вектор, проведенный от заряда Q, к точке наблюдения М (рис. 168). Согласно выражению (113.1), вектор В направлен перпендикулярно плоскости, в которой расположены векторы v и г, а именно: его направление совпадает с направлением поступательного движения правого винта при его вращении от v к г. Модуль магнитной индукции (113.1) вычисляется по формуле
,(113.2)
где a — угол междувекторами v и г.
Сравнивая выражения (110.1) и (113.1), видим, что движущийся заряд по своим магнитным свойствам эквивалентен элементу тока:
.
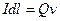Приведенные закономерности (113.1) и (113.2) справедливы лишь при малых скоростях (váác) движущихся зарядов, когда электрическое поле свободно движущегося заряда можно считать электростатическим, т. е. создаваемым неподвижным зарядом, находящимся в той точке, где в данный момент времени расположен движущийся заряд.
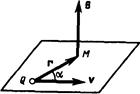Рис. 168
|
Формула (113.1) определяет магнитную индукцию положительного заряда, движущегося со скоростью v. Если движется отрицательный заряд, то Q. надо заменить на —Q. Скорость v — относительная скорость, т. е. скорость относительно наблюдателя. Вектор В в рассматриваемой системе отсчета зависиткак от времени, так и от положения точки М наблюдения. Поэтому следует подчеркнуть относительный характер магнитного поля движущегося заряда.
Впервые поле движущегося заряда удалось обнаружить американскому физику Г. Роуланду (1848—1901). Окончательно этот факт был установлен профессором Московского университета А. А. Эйхенвальдом (1863—1944), изучившим магнитное поле конвекционного тока, а также магнитное поле связанных зарядов поляризованного диэлектрика. Магнитное поле свободно движущихся зарядов было измерено академиком А. Ф. Иоффе, доказавшим эквивалентность, в смысле возбуждения магнитного поля, электронного пучка и тока проводимости.
§ 114. Действие магнитного поля на движущийся заряд
Опыт показывает, что магнитное поле действует не только на проводники с током (см. § 111), но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренца и выражается формулой
,(114.1)
где В — индукция магнитного поля, в котором заряд движется.
Направление силы Лоренца определяется с помощьюправила левой руки: если ладонь левой руки расположить так, чтобы в нее входил векторВ, а четыре вытянутых пальца направить вдоль вектора v (для Q>0 направления I и v совпадают, дня Q<0 — противоположны), то отогнутый большой палец покажет направление силы, действующей на положительный заряд. На рис. 169 показана взаимная ориентация векторов v, В (поле направлено к нам, на рисунке показано точками) и F для положительного заряда. На отрицательный заряд сила действует в противоположном направлении. Модуль силы Лоренца (см. (114.1)) равен
,
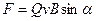где a — угол между v и В.
Отметим еще раз (см. § 109), что магнитное поле не действует на покоящийся электрический заряд. В этом существенное отличие магнитного поля от электрического. Магнитное поле действует только на движущиеся в нем заряды.
Так как по действию силы Лоренца можно найти модуль и направление вектораВ,то выражение для силы Лоренца может быть использовано (наравне с другими, см. § 109) для определения вектора магнитной индукции В.
Сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, поэтому она изменяет только направление этой скорости, не изменяя ее модуля. Следовательно, сила Лоренца работы не совершает. Иными словами, постоянное
магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изменяется.
Если на движущийся электрический заряд помимо магнитного поля с индукцией В действует и электрическое поле с напряженностью Е, то результирующая силаF,приложенная к заряду, равна векторной сумме сил — силы, действующей со стороны электрического поля, и силы Лоренца:
.
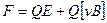Это выражение называется формулой Лоренца. Скорость v в этой формуле есть скорость заряда относительно магнитного поля.
§ 115. Движение заряженных частиц в магнитном поле
Выражение для силы Лоренца (114.1) позволяет найти ряд закономерностей движения заряженных частиц в магнитном поле. Направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле зависят от знака заряда Q, частицы. На этом основано определение знака заряда частиц, движущихся в магнитных полях.
Для вывода общих закономерностей будем считать, что магнитное поле однородно и на частицы электрические поля не действуют. Если заряженная частица движется в магнитном поле со скоростью v вдоль линий магнитной индукции, то угол a между векторами v и В равен 0 или p. Тогда по формуле (114.1) сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно.
Если заряженная частица движется в магнитном поле со скоростью v, перпендикулярной векторуВ, то сила Лоренца F=Q[vB] постоянна по модулю и нормальна к траектории частицы. Согласно второму закону Ньютона, эта сила создает центростремительное ускорение. Отсюда следует, что частица будет двигаться по окружности, радиус r которой определяется из условия
,
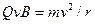откуда
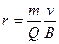(115.1)
Период вращения частицы, т. е. время Т, за которое она совершает один полный оборот,
.
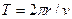Подставив сюда выражение (115.1), получим
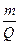(115.2)
т. е. период вращения частицы в однородном магнитном поле определяется только величиной, обратной удельному заряду (Q/т) частицы, и магнитной индукцией поля, но не зависит от ее скорости (при v<<c). На этом основано действие циклических ускорителей заряженных частиц (см. § 116).
Если скорость v заряженной частицы направлена под углом a к вектору В (рис. 170), то ее движение можно представить в виде суперпозиции: 1) равномерного прямолинейного движения вдоль поля со скоростьюvïï=vcosa; 2) равномерного движения со скоростью v^=vsina по окружности в плоскости, перпендикулярной полю. Радиус окружности определяется формулой (115.1) (в данном случае надо заменить v на v^=vsina). В результате сложения обоих движений возникает движение по спирали, ось которой параллельна магнитному полю (рис. 170). Шаг винтовой линии
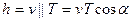
Подставив в последнее выражение (115.2), получим
.
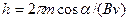Направление, в котором закручивается спираль, зависит от знака заряда частицы.
Если скорость v заряженной частицы составляет угол a с направлением вектора В неоднородного магнитного поля, индукция которого возрастает в направлении движения частицы, то r и h уменьшаются с ростом В. На этом основана фокусировка заряженных частиц в магнитном поле.
§ 116. Ускорители заряженных частиц
Ускорителями заряженных частиц называются устройства, в которых под действием электрических и магнитных полей создаются и управляются пучки высокоэнергетичных заряженных частиц (электронов, протонов, мезонов и т. д.).
Любой ускоритель характеризуется типом ускоряемых частиц, энергией, сообщаемой частицам, разбросом частиц по энергиям и интенсивностью пучка. Ускорители делятся на непрерывные (из них выходит равномерный по времени пучок) и импульсные (из них частицы вылетают порциями — импульсами). Последние характеризуются длительностью импульса. По форме траектории и механизму ускорения частиц ускорители делятся на линейные, циклические и индукционные. В линейных ускорителях траектории движения частиц близки к прямым линиям, в циклических и индукционных — траекториями частиц являются окружности или спирали.
Рассмотрим некоторые типы ускорителей заряженных частиц.
1. Линейный ускоритель. Ускорение частиц осуществляется электростатическим полем, создаваемым, например, высоковольтным генератором Ван-де-Граафа (см. § 92). Заряженная частица проходит поле однократно: заряд Q, проходя разность потенциалов j1-j2, приобретает энергию W=Q(j1-j2). Таким способом частицы ускоряются до »10МэВ. Их дальнейшее ускорение с помощью источников постоянного напряжения невозможно из-за утечки зарядов, пробоев и т. д.
2. Линейный резонансный ускоритель. Ускорение заряженных частиц осуществляется переменным электрическим полем сверхвысокой частоты, синхронно изменяющимся с движением частиц. Таким способом протоны ускоряются до энергий порядка десятков мегаэлектрон-вольт, электроны — до десятков гигаэлектрон-вольт.
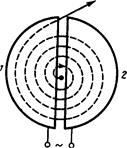
3. Циклотрон — циклический резонансный ускоритель тяжелых частиц (протонов, ионов). Его принципиальная схема приведена на рис. 171. Между полюсами сильного электромагнита помещается вакуумная камера, в которой находятся два электрода (1 и 2) в виде полых металлических полуцилиндров, или дуантов. К дуантам приложено переменное электрическое поле. Магнитное поле, создаваемое электромагнитом, однородно и перпендикулярно плоскости дуантов
Если заряженную частицу ввести в центр зазора между дуантами, то она, ускоряемая электрическим в отклоняемая магнитным полями, войдя в дуант 1, опишет полуокружность, радиус которой пропорционален скорости частицы (см. (115.1)). К моменту ее выхода из дуанта 1 полярность напряжения изменяется (при соответствующем подборе изменения напряжения между дуантами), поэтому частица вновь ускоряется и, переходя в дуант 2, описывает там уже полуокружность большего радиуса и т. д.
Для непрерывного ускорения частицы в циклотроне необходимо выполнить условие синхронизма (условие “резонанса”) — периоды вращения частицы в магнитном поле и колебаний электрического поля должны быть равны. При выполнении этого условия частица будет двигаться по раскручивающейся спирали, получая при каждом прохождении через зазор дополнительную энергию. На последнем витке, когда энергия частиц и радиус орбиты доведены до максимально допустимых значений, пучок частиц посредством отклоняющего электрического поля выводится из циклотрона.
Циклотроны позволяют ускорять протоны до энергий примерно 20 МэВ. Дальнейшееих ускорение в циклотроне ограничивается релятивистским возрастанием массы со скоростью (см. (39.1)), что приводит к увеличению периода обращения (по (115.2) он пропорционален массе), и синхронизм нарушается. Поэтому циклотрон совершенно неприменим для ускорения электронов (при E=0,5 МэВ m=2m0то, при E=10 МэВ m=28m0l).
Ускорение релятивистских частиц в циклических ускорителях можно, однако, осуществить, если применять предложенный в 1944 г. В. И. Векслером (1907—1966) и в 1945 г. американским физиком Э. Мак-Милланом (р. 1907)принцип автофазировки.Его идея заключается в том, что для компенсации увеличения периода вращения частиц, ведущего к нарушению синхронизма, изменяют либо частоту ускоряющего электрического, либо индукцию магнитного полей, либо то и другое. Принцип автофа-зировки используется в фазотроне, синхротроне и синхрофазотроне.
4. Фазотрон (синхроциклотрон) — циклический резонансный ускоритель тяжелых заряженных частиц (например, протонов, ионов, a-частиц), в котором управляющее магнитное* поле постоянно, а частота ускоряющего электрического поля медленно изменяется с периодом. Движение частиц в фазотроне, как и в циклотроне, происходит по раскручивающейся спирали. Частицы в фазотроне ускоряются до энергий, примерно равных 1 ГэВ (ограничения здесь определяются размерами фазотрона, так как с ростом скорости частиц растет радиус их орбиты).
5. Синхротрон — циклический резонансный ускоритель ультрарелятивистских электронов, в котором управляющее магнитное поле изменяется во времени, а частота ускоряющего электрического поля постоянна. Электроны в синхротроне ускоряются до энергий 5—10 ГэВ.
6. Синхрофазотрон — циклический резонансный ускоритель тяжелых заряженных
Рис. 171
частиц (протонов, ионов), в котором объединяются свойства фазотрона в синхротрона, т. е. управляющее магнитное поле и частота ускоряющего электрического поля одновременно изменяются во времени так, чтобы радиус равновесной орбиты частиц оставался постоянным. Протоны ускоряются в синхрофазотроне до энергий 500 ГэВ.
7. Бетатрон — циклический индукционный ускоритель электронов, в котором ускорение осуществляется вихревым электрическим полем (см. 5 137), индуцируемым переменным магнитным полем, удерживающим электроны на круговой орбите. В бетатроне в отличие от рассмотренных выше ускорителей не существует проблемы синхронизации. Электроны в бетатроне ускоряются до энергий 100 МэВ. При W>100МэВ режим ускорения в бетатроне нарушается электромагнитным излучением электронов. Особенно распространены бетатроны на энергии 20—50 МэВ (выпускаются серийно).
§ 117. Эффект Холла
Эффект Холла* (1879) — это возникновение в металле (или полупроводнике) с током плотностью j помещенном в магнитное поле В, электрического поля в направлении, перпендикулярном В и j.
Поместим металлическую пластинку с током плотностью j в магнитное поле В, перпендикулярное j (рис. 172). При данном направлении j скорость носителей тока в металле — электронов — направлена справа налево. Электроны испытывают действие силы Лоренца (см. § 114), которая в данном случае направлена вверх. Таким образом, у верхнего края пластинки возникнет повышенная концентрация электронов (он зарядится отрицательно), а у нижнего — их недостаток (зарядится положительно). В результате этого между краями пластинки возникнет дополнительное поперечное электрическое поле, направленное снизу вверх. Когда напряженность EB, этого поперечного поля достигнет такой величины, что его действие на заряды будет уравновешивать силу Лоренца, то установится стационарное распределение зарядов в поперечном направлении. Тогда
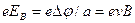, или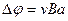 
,
где a — ширина пластинки, Dj — поперечная (холловская) разность потенциалов.
Учитывая, что сила тока I=jS= пеvS (S — площадь поперечного сечения пластинки толщиной d, п — концентрация электронов, v — средняя скорость упорядоченного движения электронов), получим
,
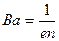
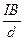
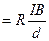Рис.172
т. е. холловская поперечная разность потенциалов прямо пропорциональна магнитной индукции В, силе тока I и обратно пропорциональна толщине пластинки d. В формуле
(117.1) R=1/(еп) — постоянная Холла, зависящая от вещества. По измеренному значению постоянной Холла можно: 1) определить концентрацию носителей тока в проводнике (при известных характере проводимости и заряде носителей); 2) судить о природа проводимости полупроводников (см. § 242, 243), так как знак постоянной Холла совпадает со знаком заряда е носителей тока. Эффект Холла поэтому — наиболее эффективный метод изучения энергетического спектра носителей тока в металлах и полупроводниках. Он применяется также для умножения постоянных токов в аналоговых вычислительных машинах, в измерительной технике (датчики Холла) и т. д.
§ 118. Циркуляция вектора В для магнитного поля в вакууме
Аналогично циркуляции вектора напряженности электростатического поля (см. § 83) введем циркуляцию вектора магнитной индукции. Циркуляцией вектора В по заданному замкнутому контуру называется интеграл
= 
,
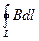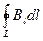где dl — вектор элементарной длины контура, направленной вдоль обхода контура, Bl=Bcosa — составляющая вектора В в направлении касательной к контуру (с учетом выбранного направления обхода), a — угол между векторами В и dl.
Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора В):циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной m0 на алгебраическую сумму токов, охватываемых этим контуром:
= 
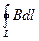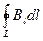
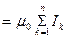,(118.1)
где n — число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток противоположного направления считается отрицательным. Например, для системы токов, изображенных на рис. 173,
.
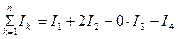Выражение (118.1) справедливо только для поля в вакууме, поскольку, как будет показано ниже, для поля в веществе необходимо учитывать молекулярные токи.
Продемонстрируем справедливость теоремы о циркуляции вектора В на примере магнитного поля прямого тока I, перпендикулярного плоскости чертежа и направлен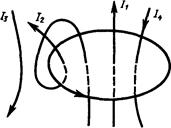 
Рис. 173
ного к нам (рис. 174). Представим себе замкнутый контур в виде окружности радиусом r. В каждой точке этого контура вектор В одинаков по модулю и направлен по касательной к окружности (она является и линией магнитной индукции). О циркуляция вектора В равна
= 
.
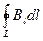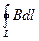
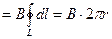Согласно выражению (118.1), получим B·2pr=m0I (в вакууме), откуда
.
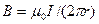Таким образом, исходяиз теоремы о циркуляции вектора В получили выражение для магнитной индукции поля прямого тока, выведенное выше (см. (110.5)).
Сравнивая выражения (83.3) и (118.1) для циркуляции векторов Е и . между ними существует принципиальное различие. Циркуляция вектора Е электростатического поля всегда равна нулю, т. е. электростатическое поле являете потенциальным. Циркуляция вектора В магнитного поля не равна нулю. Такое поле называется. вихревым.
Теорема о циркуляции вектора В имеет в учении о магнитном о значение, как теорема Гаусса в электростатике, так как позволяет находить индукцию поля без применения закона Био — Савара — Лапласа.
§ 119. Магнитные поля соленоида и тороида
Рассчитаем, применяя теорему о циркуляции, индукцию магнитного соленоида. Рассмотрим соленоид длиной l, имеющий N витков, по которому течет ток (рис. 175). Длину соленоида считаем во много раз больше, чем диаметр его витков, т. е. рассматриваемый соленоид бесконечно длинный. Экспериментальное изучение магнитного поля соленоида (см. рис. 162, б) показывает, что внутри соленоида поле является однородным, вне соленоида — неоднородным и очень слабым
На рис. 175 представлены линии магнитной индукции внутри и вне соленоида. Чем соленоид длиннее, тем меньше магнитная индукция вне его. Поэтому можно считать, что поле бесконечно длинного соленоида сосредоточен целиком внутри него, а полем вне соленоида можно пренебречь.
Для нахождения магнитной индукции В выберем замкнутый прямо тур АВСВА. как показано на рис. 175. Циркуляция вектора В по замкнутому контуру АВСDА, охватывающему все N витков, согласно (118.1), равна
.
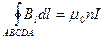Интеграл по АВСDА можно представить в виде четырех интегралов: по АВ, ВС, CD и DA:
Рис. 174
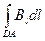
На участках АВ и СD контур перпендикулярен линиям магнитной индукции и Вl==0. На участке вне соленоида B=0. На участке DА циркуляция вектора В равна В1 (контур совпадает с линией магнитной индукции); следовательно,
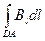
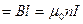(119.1)
Из (119.1) приходим к выражению для магнитной индукции поля внутри соленоида (в вакууме):
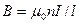(119.2)
Получили, что поле внутри соленоида однородно (краевыми эффектами в областях, прилегающих к торцам соленоида, при расчетах пренебрегают). Однако отметим, что вывод этой формулы не совсем корректен (линии магнитной индукции замкнуты, и интеграл по внешнему участку магнитного поля строго нулю не равен). Корректно рассчитать поле внутри соленоида можно, применяя закон Био — Савара — Лапласа;
в результате получается та же формула (119.2).
Важное значение для практики имеет также магнитное полетороида — кольцевой катушки, витки которой намотаны на сердечник, имеющий форму тора (рис. 176). Магнитное поле,как показывает опыт, сосредоточено внутри тороида, вне его поле отсутствует.
Линии магнитной индукции в данном случае,как следует из соображений симметрии, есть окружности, центры которых расположены по оси тороида. В качестве контура выберем одну такую окружность радиуса г. Тогда, по теореме о циркуляции (118.1), откуда следует, что магнитная индукция внутри тороида (в вакууме)
,
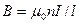
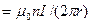где N — число витков тороида.
Если контур проходит вне тороида, то токов он не охватывает и В·2pr=0. Это означает, что поле вне тороида отсутствует (что показывает и опыт).
Дата добавления: 2017-08-01; просмотров: 253;