Найпростішою формою центральної граничної теореми є інтегральна та локальна теореми Муавра-Лапласа, які були строго доведені Лапласом у XIX сторіччі.
Умова Ліндеберга
Умова (26.1) є достатньою умовою для виконання теореми Ляпунова. Необхідною та достатньою умовою виконання центральної граничної теореми є умова Ліндеберга. Якщо для послідовності 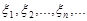 незалежних випадкових величин, для яких М
незалежних випадкових величин, для яких М 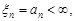
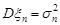 , n = 1, 2,... виконується
, n = 1, 2,... виконується
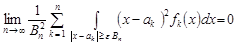 ,
, 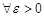 ,
,
то має місце теорема Ляпунова.
З’ясуємо ймовірнісний зміст умови Ліндеберга. Розглянемо випадкові події 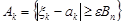 ,
, 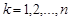 . Тоді
. Тоді
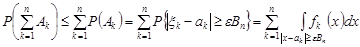 .
.
Зауважимо, що нерівність 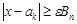 рівносильна нерівності
рівносильна нерівності 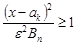 . Таким чином,
. Таким чином,
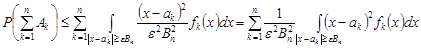 .
.
Із умови Ліндеберга випливає, що ймовірність 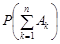 прямує до нуля при
прямує до нуля при 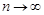 . Це означає, що кожен доданок
. Це означає, що кожен доданок 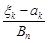 вносить рівномірно малий вклад у загальну суму
вносить рівномірно малий вклад у загальну суму 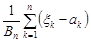 .
.
Інтегральна теорема Муавра-Лапласа
Найпростішою формою центральної граничної теореми є інтегральна та локальна теореми Муавра-Лапласа, які були строго доведені Лапласом у XIX сторіччі.
Теорема Муавра-Лапласа (інтегральна). Нехай проводиться n незалежних випробувань, у кожному з яких може з’явитися з імовірністю р деяка подія А. Якщо кількість появ події А дорівнює m, 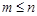 , то рівномірно для всіх
, то рівномірно для всіх 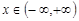
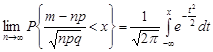 , (26.3)
, (26.3)
де 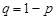 .
.
Доведення. Нехай випадкова величина 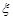 задає кількість появ події А в n незалежних випробуваннях. Введемо випадкові величини
задає кількість появ події А в n незалежних випробуваннях. Введемо випадкові величини 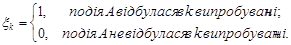 Тоді
Тоді 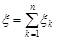 , математичне сподівання
, математичне сподівання 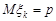 , дисперсія
, дисперсія 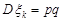 ,
, 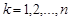 . Знайдемо третій центральний момент
. Знайдемо третій центральний момент
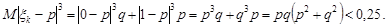
Очевидно для послідовності 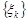 ,
, 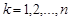 виконується умова (26.1) теореми Ляпунова:
виконується умова (26.1) теореми Ляпунова:
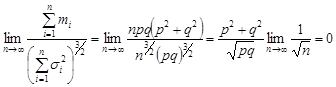 .
.
Отже, функція розподілу центрованої нормованої випадкової величини 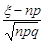 при
при 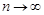 прямує до функції розподілу закону Гаусса з параметрами 0 та 1. Це означає виконання співвідношення (26.3).
прямує до функції розподілу закону Гаусса з параметрами 0 та 1. Це означає виконання співвідношення (26.3).
Мають місце такі важливі наслідки з цієї теореми:
1. Для достатньо великих 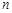 має місце наближена формула
має місце наближена формула
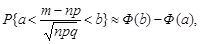 (26.4.)
(26.4.)
де Ф(х) – функція Лапласа.
Доведення. Оскільки ймовірність попадання нормальної випадкової величини 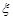 в проміжок
в проміжок 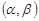 обчислюється за формулою
обчислюється за формулою 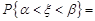
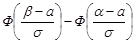 , то, враховуючи нормованість та центрованість випадкової величини
, то, враховуючи нормованість та центрованість випадкової величини 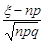 маємо формулу (26.4).
маємо формулу (26.4).
2. Імовірність того, що кількість появ події 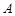 в n незалежних випробуваннях буде в межах від
в n незалежних випробуваннях буде в межах від 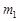 до
до 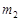 наближено дорівнює
наближено дорівнює
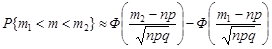 . (26.5)
. (26.5)
Доведення. У формулі (26.4) візьмемо 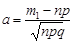 та
та 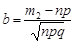 , тоді для достатньо великих
, тоді для достатньо великих 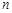
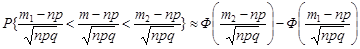 .
.
Звідки маємо формулу (26.5).
3. Використаємо формулу (26.5) для оцінки ймовірності 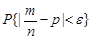 .
.
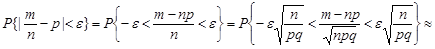
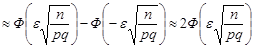 .
.
Отже, для достатньо великих 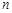 маємо наближену формулу
маємо наближену формулу
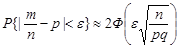 . (26.6)
. (26.6)
Ця формула дає більш точну оцінку ймовірності 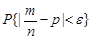 ніж нерівність Чебишева і тому на практиці користуються наближеним значення (26.6).
ніж нерівність Чебишева і тому на практиці користуються наближеним значення (26.6).
Приклад 26.1. Продукція вищого сорту складає 60 % всієї продукції. Приймальник бере 200 виробів. Яка ймовірність того, що виробів вищого сорту серед відібраних буде від 120 до 150?
Розв’язання. Імовірність того, що продукція буде вищого сорту дорівнює 0,6. Тоді величина np = 120, а npq = 48. За формулою (26.5)
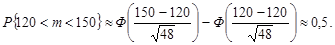
Отже, з імовірністю, яка дорівнює 0,5, можна стверджувати, що серед 200 виробів вищого сорту буде від 120 до 150 виробів.
Приклад 26.2. Скільки разів треба підкинути монету, щоб з імовірністю, яка дорівнює 0,997, частота появи герба відрізнялась би від імовірності появи герба не більше ніж на 0,5 %?
Розв’язання. Використаємо формулу (26.6), в якій візьмемо 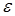 =0,005; p=q=0,5;
=0,005; p=q=0,5; 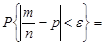 0,997.
0,997.
Маємо 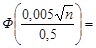 0,4985. За таблицею значень функції Лапласа знаходимо, що значенню 0,4985 наближено відповідає аргумент 2,97, тобто
0,4985. За таблицею значень функції Лапласа знаходимо, що значенню 0,4985 наближено відповідає аргумент 2,97, тобто 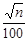 =2,97. Звідки
=2,97. Звідки 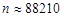 .
.
Дата добавления: 2017-02-20; просмотров: 736;
