Вероятность и неопределенность

Если у вас неверные факты, но безупречная логика, ваши заключения неизбежно будут ложными. Поэтому, делая логические ошибки, вы получаете хотя бы случайный шанс прийти к правильному заключению.

Теорема Кристи—Дэвиса (источник неизвестен, взято из календаря)

Если я подброшу «честную» монету (т.е. монету, для которой выпадение орла и решки одинаково вероятно) и попрошу вас угадать вероятность выпадения орла, вы скажете, что она равна 50% (или 0,50). Это означает, что ожидается, что монета будет падать орлом вверх в половине случаев. Несмотря на то, что слово вероятность используется в нескольких различных значениях, в контексте данной главы полезнее всего будет такое определение: вероятностью называется отношение числа способов, которыми можно прийти к определенному исходу (мы называем его успехом), к числу возможных исходов (когда все они равноправны). Это мера того, насколько часто мы ожидаем появления этого события в достаточно протяженном интервале времени. Слово «успех» может показаться странным в данном контексте, но вы можете считать, что это исход, в котором вы заинтересованы. В нашем примере успех — это выпадение орла. Монета может упасть орлом вверх только одним способом, поэтому число способов, которыми можно прийти к успеху, равно 1. Каковы все возможные исходы подбрасывания монеты? Монета может упасть или орлом вверх, или решкой вверх. (Я никогда не видела, чтобы монета приземлялась на ребро, а также никогда не видела, чтобы птица поймала монету в воздухе и унесла ее, поэтому я не рассматриваю такие исходы в качестве возможных.) Таким образом, существует только два возможных исхода, каждый из которых равноправен. Чтобы подсчитать вероятность выпадения орла, поделите количество способов выпадения орла (1) на число возможных исходов (2) и вы получите ½, ответ, который был вам уже известен. Поскольку некоторым людям легче воспринимать проценты, чем дроби, иногда ½ заменяют на 50%. Таким образом, вы можете ожидать, что орел будет выпадать в 50% случаев, в достаточно протяженном интервале времени (т. е., в данном случае при большом числе попыток).

Давайте рассмотрим другой пример. Какова вероятность выпадения пяти при одном броске игральной кости? Поскольку 5 может выпасть только одним способом, числитель вероятностной дроби будет равен 1. Игральная кость — это шестигранный куб; поэтому при броске существует шесть возможных исходов. Если кость не «утяжелена» — т.е. может упасть любой стороной вверх с одинаковой вероятностью, — вероятность выпадения пяти равна 1/₆ или примерно 17%. (302:)

Какова вероятность выпадения четного числа при одном броске «честной» кости? Чтобы найти ее, рассмотрим количество способов, которыми можно прийти к успеху. Может выпасть 2, 4 или 6 — других возможных четных чисел нет. Таким образом, к успеху можно прийти тремя способами из шести равновероятных исходов, поэтому вероятность выпадения четного числа равна ³/_б = ½.

Какова вероятность выпадения целого числа меньше семи? Если бы меня попросили поставить на это событие, я бы поставила свой дом, своих детей и все свои скромные сбережения. Другими словами, я ручаюсь, что это обязательно произойдет. Давайте выясним, почему. Количество способов, которыми при одном броске кости может выпасть число меньше семи, равно шести (1, 2, 3, 4, 5 или 6), и число возможных исходов равно шести. Таким образом, вероятность равна ⁶/₆ или 1. Когда вероятность равна 1 (или 100%), событие должно произойти; оно достоверно.

Какова вероятность выпадения восьми при одном броске кости? Я бы снова поставила все, что имею, но только против того, что это произойдет. Количество способов, которыми может выпасть 8, равно 0. Следовательно, вероятность этого события равна нулю; это событие невозможно. Такая ситуация также отражает полную определенность. Значения вероятности находятся в диапазоне от 0 (событие не может произойти) до 1 (событие должно обязательно произойти). Значения вероятности, близкие к 0 или 1, характеризуют события, которые почти точно не произойдут или почти точно произойдут, в то время как значения, близкие к 0,5 (50%), отражают максимальную неопределенность, поскольку равновероятны оба исхода, и поэтому нет оснований предсказывать наступление одного из них. Эти соотношения иллюстрирует рис. 7.1.

Шансы

Часто удобно обсуждать вероятности, пользуясь понятием «шансы». Допустим, ваш друг говорит, что шансы футбольной команды его школы победить команду вашей школы равны 1 к 3. Он ожидает, таким образом, что если бы было проведено четыре игры, то его команда выиграла бы три из них. Обычно знатоки спорта (спортивные комментаторы, редакторы спортивных газет и просто болельщики) выражают степень своей уверенности в исходе спортивных состязаний, пользуясь терминологией шансов. (Ставки, которые принимаются на скачках и матчах по боксу, отражают количество денег, поставленное на каждого претендента, и, следовательно, их смысл несколько отличается от описанного выше.)

Чтобы перевести шансы в вероятности, сложите два приведенных числа (например, 3:1 = 4), возьмите первое число в качестве числителя, а полученную сумму в качестве знаменателя (³/₄) и вы получите эквивалентную вероятность.

Законы случая

Самыми важными в последнем разделе были слова «в достаточно протяженном интервале времени». Кроме особых случаев, когда вероятность исхода равна 0% или 100%, мы не можем с определенностью сказать, что произойдет в каждый кон-

Пример

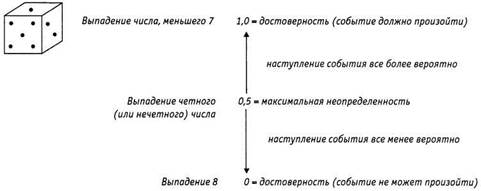
Рис 7.1. Вероятность и достоверность.

кретный момент. Бросая кость, я не знаю, выпадет ли 5, но если я буду бросать «честную» кость много-много раз, я знаю, что 5 будет выпадать примерно в 17% случаев. Я не знаю, при каких именно бросках будет выпадать 5, но я приблизительно знаю, сколько испытаний окончатся выпадением 5, если я буду бросать кость в течение долгого времени. Это важно отметить. Когда мы говорим о законах случая (или законах вероятностей), мы имеем в виду способность предсказывать долю или процент попыток, которые будут иметь данный исход. При большом количестве попыток я могу очень точно предсказать количество появлений данного исхода, но я не могу знать, какие именно попытки дадут этот исход. Это означает, что я могу делать хорошие «долгосрочные прогнозы» и плохие «краткосрочные» прогнозы.

Давайте разберемся в этих различиях на примере страхования. Когда вы страхуете свою жизнь (или что-либо еще), вы заключаете пари со страховой компанией. Вы соглашаетесь ежегодно платить страховой компании определенную сумму. Она соглашается выплатить вашим наследникам определенную сумму, когда вы умрете. Существует много различных видов полисов страхования жизни, но в наших целях нам достаточно рассмотреть простейший из них. Для демонстрации статистических идей я воспользуюсь простыми числами — в реальной жизни затраты и выплаты не такие, как в этом примере. Предположим, что вам 30 лет и вы согласились платить страховой компании 1000 долларов в год. Когда вы умрете, ваши наследники получат 20 000 долларов. Вы ставите на то, что умрете в довольно молодом возрасте (пари, которое вы надеетесь проиграть), так что вы выплатите компании лишь небольшую часть суммы, которую затем получат ваши наследники. Если вы умрете, не дожив до 50 лет, то вы выиграете. Если не обращать внимания на такие усложняющие вычисления факторы, как инфляция и проценты с капитала, то, скончавшись в молодом возрасте, вы заплатите меньше тех 20 000 долларов, которые получат ваши наследники. С другой стороны, страховая компания выиграет, если вы доживете до глубокой старости. Если вы умрете в возрасте семидесяти лет, то заплатите компании 40 000 долларов, а ваши близкие получат только 20 000. (304:)

Страховые компании зарабатывают деньги на законах случая (законах вероятностей). Никто не знает, когда умрете вы или кто-либо другой, но страховые компании знают примерное число тридцатилетних людей (возраст, когда вы купили свой полис), которые умирают, не дожив до пятидесяти. Таким образом, хотя никто не может точно предсказать, в каком возрасте умрет тот или иной человек, мы можем пользоваться законами случая для прогнозирования числа людей, которые доживут до того или иного конкретного возраста.