Проверка гипотезы об однородности двух независимых выборок

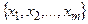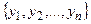Приведём описание алгоритма проверки гипотезы об однородности двух независимых выборок и т.е. гипотезы о том, что непрерывные с.в. 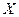и 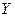распределены по одному закону. Предполагается, что объём первой выборки не больше объёма второй выборки, т.е. .

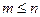Для проверки этой гипотезы используется критерий Вилкоксона. Согласно этому критерию требуется произвести следующие действия:

1) смешать элементы обеих выборок, расположить их в порядке возрастания и найти наблюдаемое значение критерия 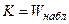— сумму порядковых номеров элементов первой выборки в получившейся последовательности.

2) найти по таблице Вилкоксона нижнюю критическую точку

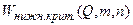, где .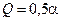

3) найти верхнюю критическую точку по формуле

.

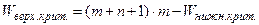Областью принятия гипотезы будет интервал

.

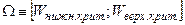Если критерий 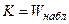попадает в этот интервал, гипотеза об однородности двух выборок принимается.

Пример.

При уровне значимости 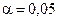проверить нулевую гипотезу об однородности двух выборок объёмом 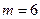и 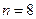(т.е. проверить, гипотезу о том, что две непрерывные случайные величины, одна из которых была измерена 6 раз, а другая 8 раз, имеют одинаковый закон распределения), если

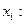
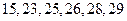
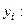
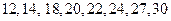
Решение. Следуя описанию алгоритма, расположим элементы обеих выборок в порядке возрастания и пронумеруем их.

Таблица

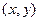
В нижней строке стоят элементы двух выборок в порядке возрастания, в верхней строчке стоят порядковые номера элементов первой выборки, во второй строке — порядковые номера элементов второй выборки.

Найдем, опять следуя описанию, наблюдаемое значение критерия в данной задаче: сумму порядковых номеров элементов первой выборки (они расположены в верхней строке).

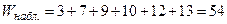
По таблице "Критические точки критерия Вилкоксона", имеющейся почти во всех учебниках по математической статистике, находим нижнюю границу области принятия гипотезы

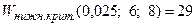
По формуле

,

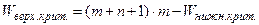Где в данном случае ,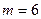

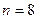
находим верхнюю границу области принятия гипотезы.

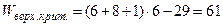
Критерий 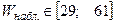, т.е. лежит в области принятия гипотезы.

Следовательно, нет оснований отвергнуть нулевую гипотезу об однородности выборки.