Вероятность справедливости этой гипотезы запишется как

.

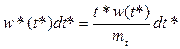Будем искать плотность распределения q при условии справедливости сформулированной гипотезы. Эту условную плотность обозначим .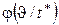

Нет оснований считать какой-то участок интервала t*, на который упала точка S, более вероятным для положения этой точки, чем другой. Поэтому точка S на интервале t* будет распределена равномерно и условная плотность 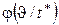тоже будет равномерна

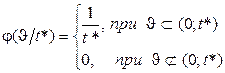. (1.19)

Совместная плотность q и T* имеет вид:

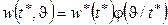. (1.20)

Безусловная плотность:

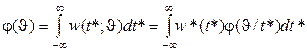. (1.21)

С учетом (1.19) подынтегральная функция отлична от нуля при 0£ 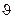£ t* , т.е. при t*> 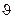. Поэтому (1.21) преобразуется к виду

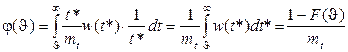, (1.22)

где F(x) - функция распределения случайной величины T.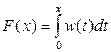

Итак: 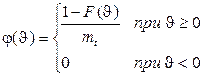. (1.23)

Здесь 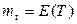- математическое ожидание случайной величины T.

Найдем числовые характеристики случайной величины q через её характеристическую функцию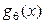

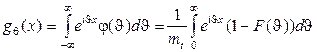. (1.24)

Интеграл в (1.24) можно вычислить по частям. Обозначая

, ,

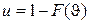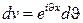имеем , .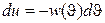

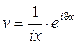Теперь

,

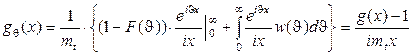где g(x) – характеристическая функция случайной величины T (как преобразование Фурье w(t)).

Напомним, что согласно (1.11) , ,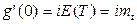

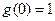поэтому: 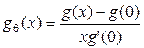. (1.25)

Найдем 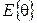и .

.

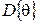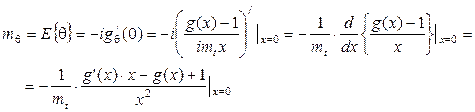Если в последнем выражении подставить 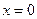, то получится неопределенность типа 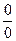. Раскроем её по правилу Лопиталя. .

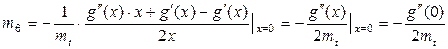Согласно формуле (1.14)

,

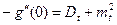поэтому 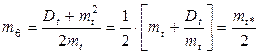(1.26)

(после третьего знака равенства учтена формула (1.17)).

Следовательно, математическое ожидание остатка 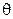всегда не меньше, чем половина математического ожидания любого интервала между событиями в стационарном потоке Пальма.

Поступая аналогично, найдем дисперсию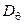

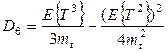. (1.27)

В заключение параграфа заметим, что случайные величины Н и q зависимы (вследствие соотношения 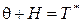, см. рис.1.5), а закон распределения Н такой же, как у q.