Вывод формулы Пуассона через производящую функцию.

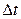Рассмотрим поток событий, обладающий свойствами ординарности и отсутствия последействия. Пусть - веро-ятность того, что за малый интервал времени , примы-кающий к моменту времени t, произойдет n событий. Очевидно 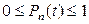, и будем считать, что выполняется условие нормировки 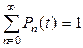. Опишем динамику изменения вероят-ности состояния потока за время 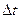. Для n=0 (отсутствие событий на интервале 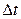) можно записать:

. (1.38а)

Множитель 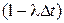является в силу ординарности потока вероятностью того, что за интервал 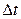не произойдет ни одного события. Для любого согласно формуле полной вероятности аналогично (1.38а) запишем

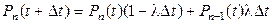. (1.38б)

Из последнего выражения легко получить

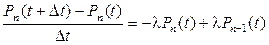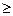для n 1.

При 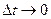слева получается производная 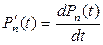, и в соответствие с этим выражения (1.38а) и (1.38б) можно переписать в дифференциальной форме.

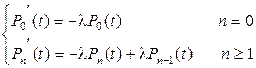. (1.39)

Это - дифференциально-разностные уравнения, которые удоб-но решать, используя производящую функцию. По определению производящая функция является Z – преобразованием распре-деления вероятностей и записывается в виде:

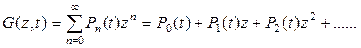, (1.40)

где z – любое комплексное число, котороедает сходимость сум-мы в (1.40).

Из (1.40) следует, что если 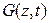продифференцировать n раз по z, то можно найти , положив z=0, т.е.

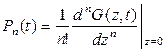. (1.41)

При решении уравнений начало отсчета времени можно выбирать произвольно, даже после того, как произойдет некоторое число событий. Возможно, что при t=0 уже произошло i событий. Тогда:

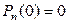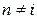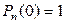при ,

при .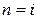

Таким образом

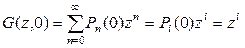. (1.42)

Из определения 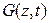также следует:

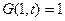, (1.43)

и 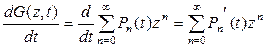. (1.44)

Умножим систему (1.39) на 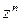(первое уравнение на 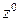) и про-суммируем по n, тогда получим:

.

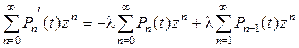Слева от знака равенства согласно (1.44) записана производная 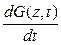. Первое слагаемое справа очевидно имеет вид , а второе представляется как

.

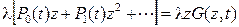В итоге получаем дифференциальное уравнение

,

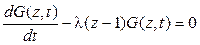которое, как известно, имеет решение:

.

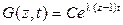Константа C определяется из начальных условий. Пусть при t=0 не было ни одного события. Тогда из (1.42) следует, что 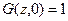т.к. i=0. Поэтому С=1. Окончательно получаем:

. (1.45)

Теперь воспользуемся формулой (1.41) :

,

,

.

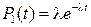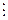
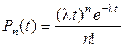Последняя формула совпадает с распределением Пуассона, где t интерпретируется как интервал (0,t).