B) Приведение формулы, полученной по утверждениям 1б(1а) приведенным к нормальным формам
(A1, A2, …, AnᅣB)↔( ᅣ (A1&A2& …&An→B))
По набору посылок и заключений строит формулу A1&A2&…&An→B, которая приводится к КНФ (можно и к ДНФ, а можно и просто упрощать). Если в результате преобразований формула A1&A2&…&An→B тождественно истинна, то логическое следование имеет место. Во всех других случаях логического следования нет.
C) Анализ от противного – анализ, исходящий из предположения, что заключение не является логическим следствием системы высказываний, т.е. предполагается, что существует, по крайней мере, хотя бы один набор истинностных значений переменных, входящих в систему
А1, А2, …, АnᅣВ,
на котором высказывания-посылки истинны, а заключение ложно.
А1 – и
А2 – и
А3 – и
…
Аn – и
В - л
Последовательно по формулам проводим анализ возможных значений переменных, набор которых обеспечивает выполнение предположения. Анализу подвергаются все формулы, начиная с формулы В. порядок использования формул-посылок в разных «ветвях» анализа может быть разным. После рассмотрения всех формул при всех возможных, исходя из предположения значения переменных, будет иметь место одна из двух ситуаций:
- при каждом возможном, исходя из предположения, наборе значения переменных будет получено противоречие с нашим предположением, что формула В не является логическим следствием посылок А1, А2, …, Аn, т.е. одна из предпосылок не может иметь значение «и». В этом случае логическое следование имеет место. Все ветки анализа заканчиваются противоречием – логическое следование имеет место.
- рассмотрены все формулы, и при каком-либо наборе значений переменных (по крайней мере, одном) противоречие не получено. В этом случае логического следования нет. Найденные наборы истинностных значений переменных, не приводящие к противоречию (являются опровергающим примером). Процесс анализа оформляется в виде дерева с ветвлениями по различным возможным значениям переменных. Получение ситуации отсутствия противоречия хотя бы на одной из ветвей дерева анализа позволяет сформулировать ответ «В не является логическим следствием высказываний А1, А2, …, Аn», не строя другие ветви. Хотя анализ может быть продолжен для нахождения других опровергающих примеров.
D) Прямой анализ – анализ, исходящий из предположения, чтоформула-заключение В является логическим следствием системы высказываний, т.е. предполагается, что на всех наборах истинностных значений переменных, входящих в систему
А1, А2, …, АnᅣВ,
на которых высказывания-посылки истинны, заключение тоже истинно.
А1 – и
А2 – и
А3 – и
…
__Аn – и__
В - и
Проводится анализ возможных значений переменных, обеспечивающих выполнение предположения. Анализу подвергаются все формулы-посылки в произвольном порядке, заключение анализируется в последнюю очередь. После рассмотрения всех формул при всех возможных, исходя из предположения, значениях переменных, будет иметь место одна из двух ситуаций:
1. По крайней мере, при одном наборе значений переменных все посылки имеют значение «и», а заключение - «л». В этом случае логическое следование не имеет места. Получен опровергающий пример. При оформлении анализа в виде дерева, при получении такого противоречия по одной из веточек, дальнейший анализ не обязателен, но может проводиться с целью получения других опровергающих примеров.
2. На каждом наборе значений переменных, где формулы-посылки А1, А2, …, Аn истинны, формула-заключение В также имеет значение «истина». В этом случае логическое следование имеет место. При оформлении анализа в виде дерева должны быть рассмотрены все ветви анализа, если противоречие не обнаруживается.
Пример 1.Определить, A®B , C®D , AÚC ᅣ B&D
Табличный метод доказательства.
Составляем таблицу истинности для системы высказываний, состоящую из 16 (24) строк (табл. 1.11)
Таблица 1.11
| А | В | C | D | A®B | C®D | AÚC | B&D |
| Л | Л | Л | Л | И | И | Л | Л |
| Л | Л | Л | И | И | И | Л | Л |
| Л | Л | И | Л | И | Л | И | Л |
| Л | Л | И | И | И | И | И | Л (!) |
| Л | И | Л | Л | И | И | Л | Л |
| Л | И | Л | И | И | И | Л | И |
| Л | И | И | Л | И | Л | И | Л |
| Л | И | И | И | И | И | И | И |
| И | Л | Л | Л | Л | И | И | Л |
| И | Л | Л | И | Л | И | И | Л |
| И | Л | И | Л | Л | Л | И | Л |
| И | Л | И | И | Л | И | И | Л |
| И | И | Л | Л | И | И | И | Л (!) |
| И | И | Л | И | И | И | И | И |
| И | И | И | Л | И | Л | И | Л |
| И | И | И | И | И | И | И | И |
Анализ таблицы производится методом последовательного отсечения строк, содержащих ложные значения формул-посылок. Т.о., перед анализом формулы-заключения, выделены все строки, где формулы-посылки – истинны. На всех строках, где формулы посылки истинны, определяем значения формулы-заключения.
В данном случае, существуют две строки, на которых формулы посылки истинны, а заключение ложно. Следовательно, формула B&D не является логическим следствием формул A®B , C®D , AÚC.
Доказательство приведением системы формул к нормальной формуле.
Приводим систему формул к виду:
(A®B) & (C®D) & (AÚC) ® (B&D).
Используя равносильные преобразования, приводим эту формулу к дизъюнктивной нормальной форме.
(A®B) & (C®D) & (AÚC) ® (B&D) eq
(ùAÚB)& (ùCÚD) &(AÚC) ® (B&D) eq
ù ((ùAÚB)& (ùCÚD) &(AÚC)) Ú (B&D) eq
ù (ùAÚB) Úù (ùCÚD) Úù (AÚC)) Ú (B&D) eq
(А&ùВ) Ú( C&ùD) Ú ( ùA&ùC) Ú (B&D)
В результате преобразований мы получили дизъюнктивную нормальную форму, не являющуюся тождественно истинной. Следовательно, формула-заключение не является логическим следствием формул посылок.
Доказательство методом «от противного».
Предположим, что формула-заключение не является логическим следствием формул 1-3. Следовательно, существует хотя бы один набор значений, входящих в них переменных, при котором формулы 1-3 принимают значение «истина», а формула-заключение принимает значение «ложь».
1) A®B - и
2) C®D - и
3) AÚC - и
B&D - л
В этом случае необходимо рассмотреть 3 варианта, так как любая из выше перечисленных формул принимает приписанные по предположению значения в 3 случаях. Схема анализа методом «от противного» приведена на рис. 1.1.
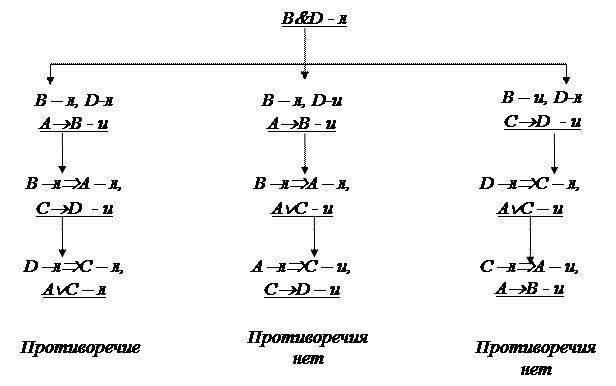 |
Рис.1.1
В первом случае было получено противоречие, а во 2 и 3 случаях противоречия не было обнаружено, следовательно, существует, по крайней мере, один набор значений переменных, входящих в формулы 1-3, при котором формула заключение является ложной. Таким набором является, например, набор B - л, D - л, A - л, C - и.
Следовательно, формула-заключение не является логическим следствием формул 1-3.
Доказательство прямым методом.
Предположим, что логическое следствие имеет место. Следовательно, на всех наборах истинностных значений переменных, где формулы-посылки истинны, заключение должно быть истинным.
A®B - И
C ®D - И
A V C – И
B&D – И
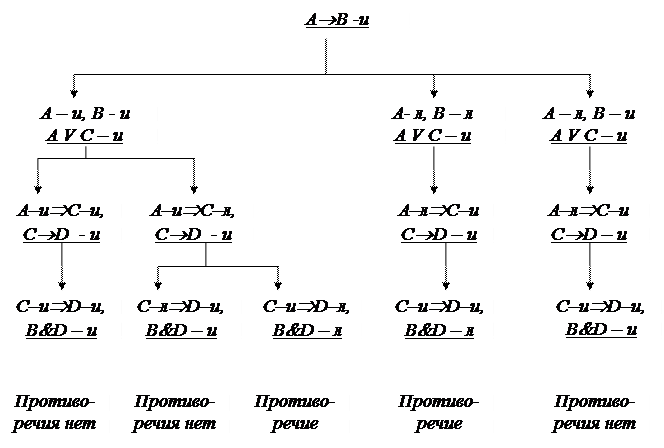 На рис. 1.2 приведена схема анализа системы высказываний прямым методом.
На рис. 1.2 приведена схема анализа системы высказываний прямым методом.
Рис.1.2
На двух наборах значений переменных, где формулы – посылки принимают значение «истина», оказалось, что формула заключение имеет значение «ложь». Следовательно, мы получили противоречие с исходным предположением, что логическое следствие имеет место, что означает, логического следования нет.
Пример 2.Определить, имеет ли место логическое следствие в следующей системе высказываний.
Если упростить схему устройства, то его стоимость снизится, а если применить новые элементы, то надежность устройства увеличится. Можно или упростить схему, или применить новые элементы. Однако, если упростить схему, то надежность не увеличивается, а если применить новые элементы, то стоимость не снижается. Значит, надежность увеличивается тогда и только тогда, когда стоимость не уменьшается.
Формализуем систему высказываний.:
1) A®B
2) C®D
3) (A&ùC)Ú(ùA&C)
4) A®ùD
5) C®ùB
D«ùB
Табличный метод доказательства.
Прежде, чем составлять таблицу истинности для системы высказываний (табл. 1.12) , отметим, что формула(A&ùC)Ú(ùA&C) равносильна формуле AÅC. Предлагаем это доказать с помощью таблиц истинности. Мы будем использовать формулу AÅC, чтобы не нагружать вспомогательными столбцами промежуточных операций таблицу истинности.
Анализ таблицы 1.12 производится методом последовательного отсечения строк, содержащих ложные значения формул-посылок. На всех строках, где формулы-посылки истинны, определяем значения формулы-заключения.
В данном случае, существуют две строки, на которых формулы посылки истинны, и на всех этих строках формула-заключение также истинна. Следовательно, логическое следствие имеет место.
Таблица 1.12
| А | В | С | D | ùB | ùD | A®B | C®D | AÅC | A®ùD | C®ùB | D«ùB |
| Л | Л | Л | Л | И | Л | И | И | Л | И | И | Л |
| Л | Л | Л | И | И | И | И | И | Л | И | И | И |
| Л | Л | И | Л | И | Л | И | Л | И | И | И | Л |
| Л | Л | И | И | И | И | И | И | И | И | И | И |
| Л | И | Л | Л | Л | Л | И | И | Л | И | И | И |
| Л | И | Л | И | Л | И | И | И | Л | И | И | Л |
| Л | И | И | Л | Л | Л | И | Л | И | И | Л | И |
| Л | И | И | И | Л | И | И | И | И | И | Л | Л |
| И | Л | Л | Л | И | Л | Л | И | И | И | И | Л |
| И | Л | Л | И | И | И | Л | И | И | Л | И | И |
| И | Л | И | Л | И | Л | Л | Л | Л | И | И | Л |
| И | Л | И | И | И | И | Л | И | Л | Л | И | И |
| И | И | Л | Л | Л | Л | И | И | И | И | И | И |
| И | И | Л | И | Л | И | И | И | И | Л | И | Л |
| И | И | И | Л | Л | Л | И | Л | Л | И | Л | И |
| И | И | И | И | Л | И | И | И | Л | Л | Л | Л |
Доказательство приведением системы формул к дизъюнктивной нормальной формуле.
Приводим систему формул к виду:
(A®B ) & (C®D ) & ((A&ùC)Ú(ùA&C) ) & (A®ùD ) & (C®ùB ) ® (D«ùB )
Используя равносильные преобразования, приводим эту формулу к дизъюнктивной нормальной форме.
(A®B )& (C®D )& ((A&ùC)Ú(ùA&C))& (A®ùD )&(C®ùB )®(D«ùB ) eq
((ùA ÚB)&(ùCÚD)& ((A&ùC)Ú(ùA&C))&(ùAÚùD)&(ùCÚùB))®(D«ùB ) eq
((ùA ÚB)&(ùCÚD)& ((A&ùC)Ú(ùA&C))&(ùAÚùD)&(ùCÚùB))® ((ùDÚùB)&(DÚB))eq
ù ((ùA ÚB)&(ùCÚD)& ((A&ùC)Ú(ùA&C))&(ùAÚùD)&(ùCÚùB)) Ú ((ùDÚùB)&(DÚB))eq
ù (ùA ÚB) Ú ù (ùCÚD) Ú ù ((A&ùC)Ú(ùA&C)) Úù (ùAÚùD) Ú ù (ùCÚùB)) Ú ((ùDÚùB)&(DÚB))eq
(A &ùB) Ú (C&ùD) Ú (ù (A&ùC)& ù (ùA&C)) Ú(A&D) Ú (C&B) Ú ((ùDÚùB)&(DÚB))eq
(A &ùB) Ú (C&ùD) Ú((ùAÚC)& (AÚùC)) Ú(A&D) Ú (C&B) Ú ((ùDÚùB)&(DÚB))eq
(A &ùB) Ú (C&ùD) Ú((ùAÚC)& (AÚùC)) Ú(A&D) Ú (C&B) Ú
((ùD&B) Ú (D&ùB))eq (перегруппируем составляющие формулы)
(A &ùB) Ú(A&D) Ú (C&ùD) Ú (C&B) Ú(ùD&B) Ú (D&ùB) Ú
((ùAÚC)& (AÚùC)) eq
(A&((ùBÚD)) Ú(C&(ùDÚB)) Úù (DÚùB) Úù (ùDÚB) Ú
((ùAÚC)& (AÚùC)) eq (перегруппируем составляющие формулы)
(A&((ùBÚD)) Úù (DÚùB) Ú(C&(ùDÚB)) Úù (ùDÚB) Ú
((ùAÚC)& (AÚùC)) eq
((AÚù (DÚùB))& ((ùBÚD)Úù (DÚùB))Ú((CÚù (ùDÚB))&
и
((ùDÚB)Úù (ùDÚB))) Ú ((ùAÚC)& (AÚùC)) eq
и
AÚù (DÚùB) ÚCÚù (ùDÚB) Ú ((ùAÚC)& (AÚùC)) eq
(AÚС) Ú((ùAÚC)& (AÚùC)) Úù (DÚùB) Úù (ùDÚB) eq
((A ÚC ÚùAÚC )&( A ÚC ÚAÚùC)) Ú (ùB&D)Ú(ùD&B) eq
(и & и) Ú (ùB&D)Ú(ùD&B) eq и
В результате преобразований мы получили тождественно истинную ДНФ, следовательно, формула-заключение является логическим следствием формул посылок.
Доказательство методом «от противного».
Предположим, что формула-заключение не является логическим следствием формул 1-5. Следовательно, существует хотя бы один набор значений, входящих в них переменных, при котором формулы 1-5 принимают значение «истина», а формула-заключение принимает значение «ложь».
1) A®B - и
2) C®D - и
3) (A&ùC)Ú(ùA&C) - и
4) A®ùD - и
5) C®ùB - и
D«ùB - л
Формулы 1-2 и 4-5 истинны в 3 случаях, а формула 3 и формула заключение принимают приписанные значения только в двух случаях (формула 3 – формула антиэквиваленции). Поэтому, имеет смысл начинать анализ с одной из этих формул. Более простой выглядит формула-заключение. Схема анализа логичности системы высказываний приведена на рис. 1.3.
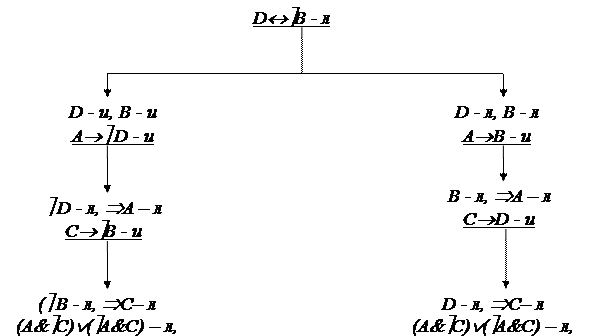 |
Рис.1.3
И в первом, и во втором случае получено противоречие с предположением, что формула-заключение не является логическим следствием, т.е. во всех случаях нет ни одного набора переменных, входящих в формулы 1-5, при котором формула-заключение была бы ложной. Таким образом, делаем вывод: логическое следствие имеет место.
Доказательство прямым методом.
Предположим, что логическое следствие имеет место. Следовательно, на всех наборах истинностных значений переменных, где формулы -посылки истинны, заключение должно быть истинным, т.е.:
1) A®B - И
2) C®D - И
3) (A&ùC) V (ùA&C) - И
4) A®ùD - И
5) C®ùВ - И
D«ùB - И
Схема анализа логичности системы высказываний приведена на рис. 1.4.

Рис. 1.4
Мы предположили, что логическое следствие имеет место, и ни на одном наборе значений переменных, входящих в систему высказываний, не получили противоречие. Следовательно, логическое следствие имеет место.
1.8.Непротиворечивость множества высказываний
Вопрос о непротиворечивости множества высказываний можно задать относительно системы посылок, предлагаемой нам для логического вывода, поскольку, если множество посылок противоречиво, то задача выявления логического следования теряет смысл. Помимо этого вопрос непротиворечивости множества высказываний имеет самостоятельное значение, так как правильности или неправильность описания какой-то ситуации для рационального его осмысления требует как минимум логической непротиворечивости.
Критерий непротиворечивости множества высказываний
Множеством высказываний {A1;A2;…An} непротиворечиво, если существует, по крайней мере, одно такое распределение истинностных значений простых компонентов формул, что все высказывания {A1;A2;…An} принимают значение «истина».
Множество высказываний {A1;A2;…An} является противоречивыммножеством, если при всяком распределении истинностных значений простых компонентов формул, по крайней мере, одна из формул получает значение «ложь», то есть
A1&A2&…&An eq Л(1)
Дата добавления: 2019-10-16; просмотров: 1145;
