Методы определения противоречивости или непротиворечивости множества высказываний
– Построение таблицы истинности
Строится таблица истинности вида
| Р1 | … | Рм | Вспомогательные столбцы | А1 | … | Ап |
Если в таблице истинности встретилась хотя бы одна строчка, в которой все формулы Aj (j=1,…,n) имеют значение «и», то система высказываний непротиворечива. Если не найдено ни одной строки, где бы все формулы принимали значение «истина», то система – противоречива.
– Приведение к дизъюнктивной нормальной форме или конъюнктивной нормальной форме.
Строится формула вида (1) и приводится к совершенной дизъюнктивной или конъюнктивной нормальной форме. Если формула (1) принимает значение «ложь», то система противоречива, в остальных случаях - непротиворечива.
Прямой анализ
Теорема: для непротиворечивости системы высказываний любая посылка является логическим следствием всего множества высказываний.
Для установления непротиворечивости множества высказываний лучше использовать «прямой анализ», т.е. анализ исходит из предположения, что система не противоречива, а следовательно существует хотя бы один набор значений входящих в систему формул переменных, при котором все формулы истинны.
Пример1. Исследовать систему высказываний на непротиворечивость.
А®ù (В & С)
(DÚ E) ®F
F®ù (G Ú H)
ùC & E & F
Табличный способ исследования системы высказываний на противоречивость мы рассматривать не будем, т.к. в систему входит 8 переменных, а, следовательно, количество строк в таблице должно быть 28=256. Поэтому далее применим более эффективные методы исследования системы на противоречивость.
Доказательство прямым методом. Предположим, что система высказываний непротиворечива, т.е. существует, по крайней мере, одно такое распределение истинностных значений переменных, входящих в систему высказываний, что все формулы принимают значение «истина». Схема анализа системы высказываний на непротиворечивость приведена на рис. 1.5.
Мы не стали здесь порождать ветки по значениям переменной D, т.к. формула А®ù (В & С)от D не зависит.
Т.о., существует, по крайней мере, один набор значений переменных, входящих в систему высказываний, на котором все формулы истинны.

Рис. 1.5
На самом деле мы нашли 8 наборов переменных, при которых система высказываний истинна:
| С – Л Е – И F – И G – Л Н – Л D – И В – И А - И | С – Л Е – И F – И G – Л Н – Л D – И В – И А - Л | С – Л Е – И F – И G – Л Н – Л D – И В – Л А - И | С – Л Е – И F – И G – Л Н – Л D – И В – Л А - Л | С – Л Е – И F – И G – Л Н – Л D – Л В – И А - И | С – Л Е – И F – И G – Л Н – Л D – Л В – И А - Л | С – Л Е – И F – И G – Л Н – Л D – Л В – Л А - И | С – Л Е – И F – И G – Л Н – Л D – Л В – Л А - Л |
Доказательство приведением формулы - конъюнкции системы высказываний к КНФ.
(А®ù (В & С)) & ( (DÚ E) ®F) & (F®ù (G Ú H)) & (ùC & E & F) eq
(ùA Ú ù В Ú ù С) & ((ùD & ùE) Ú F) & (ùF Ú (ù G & ù H)) & ùC & E & F eq
(ùA Ú ù В Ú ù С) & ùC & ((ùD & ùE) Ú F) & (ùF Ú (ù G & ù H)) & E & F eq
ùC & ((ùD & ùE) Ú F) & (ùF Ú (ù G & ù H)) & E & F eq
ùC & ((ùD & ùE) Ú F) & F & (ùF Ú (ù G & ù H)) & E eq
ùC & F & (ùF Ú (ù G & ù H)) & E eq ùC & ((F & ù F) Ú (ù F & ù G & ù H) &E eq ùC & (Л Ú (ù F & ù G & ù H) &E eq ùC & ù F & ù G & ù H &E
Конъюнкция системы высказываний является выполнимой, т.е. существуют наборы переменных, при которых система высказываний истинна. Следовательно, система высказываний непротиворечива.
Пример2. Исследовать систему высказываний на непротиворечивость.
(A®B& C) & ( D®B & E)
((F®ù A) & G)®H
(C®H) ® (F& D)
ù (ù C®E)
Доказательство прямым методом. Предположим, что система высказываний непротиворечива, т.е. существует, по крайней мере, одно такое распределение истинностных значений переменных, входящих в систему высказываний, при котором все формулы принимают значение «истина». Схема анализа системы высказываний на непротиворечивость приведена на рис. 1.6.
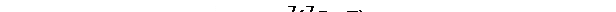
Рис. 1.6
Мы предположили, что существует хотя бы один набор, где все формулы истинны и пришли к противоречию. Следовательно, эта система высказываний противоречива.
Доказательство приведением формулы - конъюнкции системы высказываний к КНФ.
((A®B& C) & ( D®B & E)) & (((F®ù A) & G)®H) & ((C®H) ® (F& D))&
(ù (ù C®E)) eq
(ùA Ú (B&C)) & (ùD Ú (B& E)) & (ù ((ùF Ú ù A) & G) ÚH) &(ù (ù C Ú H) Ú (F&D)) &
(ù ( CÚE)) eq
(ùA Ú (B&C)) & (ùD Ú (B & E)) & ((F & A) Ú ù G Ú H)& ((C &ù H) Ú (F&D)) &
ù C& ù E eq
((ùA & ù C) Ú (B &C & ù C)) & ((ùD &ù E) Ú(B& E & ùE)) &((F & A) Ú ù G Ú H)& ((C &ù H) Ú (F&D)) eq
(ùA & ù C) &(ùD &ù E) &((F & A) Ú ù G Ú H)& ((C &ù H) Ú (F&D)) eq
ùA & ù C &ùD &ù E &((F & A) Ú ù G Ú H)& ((C &ù H) Ú (F&D)) eq
ùA &ùD &ù E &((F & A) Ú ù G Ú H)& ((C &ù H & ùC) Ú (F&D& ùC)) eq
ùA &ùD &ù E &((F & A) Ú ù G Ú H)& (F&D& ùC) eq
ùA & ùD &ù E &((F & A) Ú ù G Ú H)& F&D& ùC eq Л
Конъюнкция системы высказываний в результате приведения к КНФ оказалась тождественно ложной. Следовательно, система высказываний противоречива.
Вопросы для самопроверки к главе 1.
1. Понятие высказывания, элементарное высказывания, составные высказывания
2. Сентенциальные связки, логические операции, порядок выполнения логических операций.
3. Таблицы истинности для логических операций.
4. Понятие равносильных формул.
5. Равносильные преобразования.
6. Понятие двойственных операций, двойственных формул.
7. Соотношение равносильности для прямых и двойственных формул.
8. Понятие тавтологии, противоречия и выполнимой формулы.
9. Связь эквиваленции и равносильности.
10. Элементарная дизъюнкция, элементарная конъюнкция.
11. Конъюнктивная нормальная форма, дизъюнктивная нормальная форма.
12. Совершенная конъюнктивная нормальная форма, совершенная дизъюнктивная нормальная форма.
13. Алгоритм приведения к СКНФ, СДНФ.
14. Понятие логического следствия.
15. Доказательство логического следствия с помощью таблиц истинности.
16. Доказательство логического следствия прямым методом.
17. Доказательство логического следствия от противного.
18. Доказательство логического следствия приведением к ДНФ.
19. Понятие непротиворечивости системы высказываний.
20. Доказательство непротиворечивости системы высказываний с помощью таблиц истинности.
21. Доказательство непротиворечивости системы высказываний прямым методом.
22. Доказательство непротиворечивости системы высказываний от противного.
23. Доказательство непротиворечивости системы высказываний приведением к КНФ.
Упражнения к главе 1.
1. Среди следующих предложений определить, какие из них являются высказываниями, а какие не являются высказываниями. Для высказываний установить, истинны они или ложны.
a) Река Волка впадает в Каспийское море.
b) Всякий человек имеет брата.
c) Пейте томатный сок!
d) Существует человек, который моложе своего отца.
e) Который час?
f) Ни один человек не весит более 1000 кг.
g) 23 <5
h) Для всех действительных чисел справедливо равенство х+у = у+х
i) Х2 – 7Х +12.
j) Х2 – 7Х +12=0.
2. Формализовать следующие высказывания.
a) 45 кратно 3, и 42 кратно 3.
b) 45 кратно трем или 12 не кратно 3.
c) 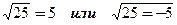
d) Если число 212 делится на 3 и 4, то оно делится на 12.
e) Число 212 – трехзначное и кратно3 или 4.
f) Число 1269 делится на 9 тогда и только тогда, когда 18 делится на 9.
g) Любое натуральное число является или четным или нечетным.
3. Пусть А – высказывание «Студент Иванов изучает английский язык»,
В – высказывание «Студент Иванов успевает по математической логике».
Дать словесную формулировку высказываний:
a) А & ùB
b) A®B
c) ùB « ùA
4. Составить таблица истинности для следующих выражений.
a) ((A ® B) & (B ® C)) ® (A ® C)
b) (A & B ® C) ® (A ® (B ® C))
c) (A ® B) ® (A Ú C ® B Ú C)
d) (A ® B) ® (A & C ® B & C)
e) (A « B) & (B « C) ® (A « C)
f) (ù P V Q V (Q & (R V ù P))) « (P& ù Q) & (ù Q V (ù R & P))
g) (P ® Q) ® (S & ù P ® Q)
h) (A ® Ø ( B V C)) « A & B &C
i) (A & B ® C) « ù (A ® (B ® C))
5. С помощью таблиц истинности и с использованием формул равносильных преобразований доказать равносильность следующих пар формул.
a) X & ( X Ú Y) eq X
b) X Ú(X & Y) eq X
c) X & ( X Ú Y) & (XÚùY) eq X
d) X Ú( ùX & Y) eq X ÚY
e) (X&Y&Z)Ú(X & Y& ùZ)Ú(X& ùY&Z)Ú(X& ùY& ùZ) eq X
6. Привести формулы с помощью равносильных преобразований к виду, содержащему только операции конъюнкции, дизъюнкции, отрицания:
a) ù(ù(хÚy) →ù(x&y)
b) (X→Y) →(ùX→ùY)
c) ù(P→(Q→P))
d) ùP→(P→Q)
e) ù((X→Z) →((Y→Z) →(XÚY→Z)))
7. Определить, используя равносильные преобразования, является формула тавтологией, противоречием или выполнимой:
a) ((A ® B) & (B ® C)) ® (A ® C)
b) (A Ú B) Ú C « A Ú (B Ú C)
c) (A & B ® C) ® (A ® (B ® C))
d) (A ® B) ® (A Ú C ® B Ú C)
e) (A ® B) ® (A & C ® B & C)
f) (((A ® (B ® C)) ® ((A ® ù C) ® (A ® ù B)))
g) (A « B) & (B « C) ® (A « C)
h) ((P ® Q) ® ((S & ù P) ® Q))
8. Привести к КНФ, к ДНФ, СКНФ, СДНФ следующие формулы:
a) A&(B&C®A&B)
b) (X®Y) ®(ùX&Y)ÚùY
c) (ù(X&Y) ®ùX)& ù((X&Y) ®ùY)
d) (XÚùZ) ®(Y&Z)
e) (A&B®B&C) ®((A®B) ®(C®B))
f) (ùA®ùB) ®(B&C®A&C)
g) (ùA®C) ®ù(ùB®ùA)
9. Определить истинность логического следствия для следующих систем высказываний:
а) Увеличение денег в обращении влечет за собой инфляцию. Но рост денежной массы происходит по двум причинам: из-за денежной эмиссии или снижения товарооборота. Снижение товарооборота приводит к безработице и спаду производства. Из-за инфляции падает курс денежной единицы.
Следовательно: если увеличить денежную эмиссию и поднять производство, тогда избежим безработицы, и курс денежной единицы останется неизменным.
b) Падение авторитета власти происходит тогда и только тогда, когда нарастает анархия в обществе. Нарастание анархии в обществе равносильно появлению на политической арене безответственных политиков. Появление подобных политиков приводит к тому, что они высказывают абсурдные идеи. Высказывание политиками таких идей влечет за собой демонстрацию неспособности их управлять страной.
Следовательно: падение авторитета власти приводит к появлению политиков, не способных управлять страной.
c) Если в сети произойдет большой перепад напряжения, то сгорит предохранитель. Если предохранитель сгорит, то необходимо его заменить. Если телевизор включен в сеть, то телевизор работает нормально при условии целостности предохранителя. Если телевизор работает нормально, то я увижу «Новости».
Следовательно: я увижу «Новости» при условии целостности предохранителя, отсутствия перепада напряжения в сети и подключения телевизора к сети питания.
10. Исследовать на непротиворечивость систему высказываний.
Если конгресс отказывается принять новые законы, то забастовка не будет окончена, если только она не длится более года и президент фирмы не уходит в отставку. Либо конгресс примет новые законы, либо забастовка не окончится, хотя и продолжается более года.
2.Логика и анализ текстов
2.1. Законы логики
1. Закон тождества: всякая сущность тождественна себе.
(А = А)
2. Закон противоречия: никакое высказывание не может
быть одновременно и истинным и ложным
3. Закон исключенного третьего: для любого
высказывания истинно либо оно само, либо его отрицание (что не истинно, то ложно)
4. Закон достаточного основания: всякое принимаемое
суждение должно быть обосновано надлежащим образом (он же – закон
Лейбница)
Закон тождества
Первый и наиболее важный закон логики — это закон тождества, который был сформулирован Аристотелем в трактате «Метафизика» следующим образом: «…иметь не одно значение — значит не иметь ни одного значения; если же у слов нет значений, тогда утрачена всякая возможность рассуждать друг с другом, а в действительности — и с самим собой; ибо невозможно ничего мыслить, если не мыслить что-нибудь одно». Можно было бы добавить к этим словам Аристотеля известное утверждение о том, что мыслить (говорить) обо всем — значит не мыслить (не говорить) ни о чем.
Закон тождества утверждает, что любая мысль (любое рассуждение) обязательно должна быть равна (тождественна) самой себе, т. е. она должна быть ясной, точной, простой, определенной. Говоря иначе, этот закон запрещает путать и подменять понятия в рассуждении (т. е. употреблять одно и то же слово в разных значениях или вкладывать одно и то же значение в разные слова), создавать двусмысленность, уклоняться от темы и т п. Например, непонятен смысл фразы: «Из-за рассеянности на турнирах шахматист неоднократно терял очки». Очевидно, что по причине нарушения закона тождества появляются неясные высказывания (суждения). Символическая запись этого закона выглядит так: а →а, где а — это любое понятие, высказывание или целое рассуждение.
Когда закон тождества нарушается непроизвольно, по незнанию, тогда возникают просто логические ошибки; но, когда этот закон нарушается преднамеренно, с целью запутать собеседника и доказать ему какую-нибудь ложную мысль, тогда появляются не просто ошибки, а софизмы. Таким образом, софизм — это внешне правильное доказательство ложной мысли с помощью преднамеренного нарушения логических законов.
Приведем пример софизма: «Что лучше: вечное блаженство или бутерброд? Конечно же, вечное блаженство. А что может быть лучше вечного блаженства? Конечно же, ничто! Но бутерброд ведь лучше, чем ничто, следовательно, он лучше вечного блаженства». Попробуйте самостоятельно найти подвох в этом рассуждении, определить, где и как в нем нарушается закон тождества и разоблачить этот софизм.
Вот еще один софизм: «Спросим нашего собеседника: «Согласен ли ты с тем, что если ты что-то потерял, то у тебя этого нет?» Он отвечает: «Согласен». Зададим ему второй вопрос: «А согласен ли ты с тем, что если ты что-то не терял, то у тебя это есть?» — «Согласен», — отвечает он. Теперь зададим ему последний и главный вопрос: «Ты не терял сегодня рога?» Что ему остается ответить? «Не терял», — говорит он. «Следовательно, — торжествующе произносим мы, — они у тебя есть, ведь ты же сам вначале признал, что если ты что-то не терял, то оно у тебя есть». Попробуйте разоблачить и этот софизм, определить, где и как в данном внешне правильном рассуждении нарушается закон тождества.
Однако на нарушениях закона тождества строятся не только неясные суждения и софизмы. С помощью нарушения этого закона можно создать какой-нибудь комический эффект. Например, Николай Васильевич Гоголь в поэме «Мертвые души», описывая помещика Ноздрева, говорит, что тот был «историческим человеком», потому что где бы он ни появлялся, с ним обязательно случалась какая-нибудь «история». На нарушении закона тождества построены многие комические афоризмы. Например: «Не стой где попало, а то еще попадет». Также с помощью нарушения этого закона создаются многие анекдоты. Например:
Дата добавления: 2019-10-16; просмотров: 1585;
