Предельная теорема для суммарного потока.

Суммарный поток получается в результате «сложения» потоков. Для простейших потоков П₁ и П₂ «сложение» состоит в том, что все моменты появления событий в этих потоках относятся к одной оси времени, на которой отмечаются моменты появления событий в суммарном потоке П₁+П₂=П.

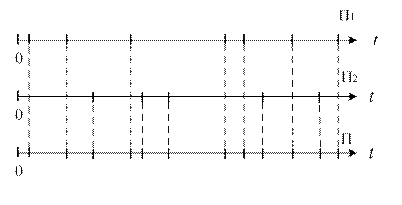
Рис.1.13. Сложение простейших потоков.

Как было установлено выше, для интенсивности суммарного потока справедливо: 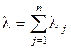, где n – число суммируемых потоков, а 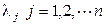- интенсивности суммируемых потоков.

Предельная теорема для суммарного потока утверждает сходимость суммы независимых, ординарных, стационарных потоков к простейшему потоку. При этом условия, налагаемые на суммируемые потоки, приблизительно такие же, как и условия ЦПТ:

- складываемые потоки должна оказывать более или менее одинаково малое влияние на суммарный поток (не должно быть потоков с очень большой ),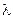

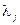- не должны при 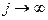становиться исчезающе малыми.

Сходимость к простейшему потоку осуществляется очень быстро (уже при 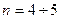). Зависимые потоки при сложение так же дают сходимость к простейшему потоку, но, естественно, при существенно большем числе слагаемых.

Сложение нестационарных потоков даёт нестаци-онарный пуассоновский поток с интенсивностью .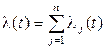

Пуассоновский поток, как было показано выше, обладает устойчивостью (то есть при суммировании пуассоновских потоков вновь получается пуассоновский поток).