Основные определения.

Потоки событий.

Основные определения.

Поток событий – последовательность событий, происхо-дящих одно за другим в случайные моменты времени. Графически поток можно отобразить так, как показано на рис.1.1, где на оси времени отмечено начало наблюдения 0 и моменты наступления событий ,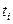

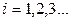
Рис.1.1. Графическое отображение потока событий

Потоки бывают однородными и неоднородными (просто самолёты или самолёты по маркам). Обычно используют однородные потоки.

Регулярный поток – события следуют одно за другим через строго определенные промежутки времени.

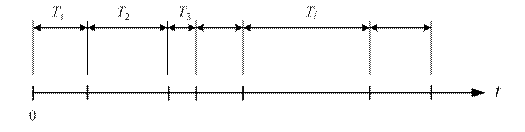
Рис.1.2. Поток событий при независимых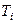

Рассмотрим поток событий, представленный на рис.1.2, где Т₁, Т₂… - случайные интервалы времени (случайные величины), независимые между собой. Такой поток называется потоком Пальма или потоком с ограниченным после-действием.

Поток называется ординарным, если для малого Δt выполняется условие:

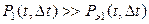, (1.1)

где 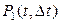- вероятность того, что за Δt произойдёт одно собы-тие и 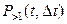- вероятность того, что за Δt произойдёт более одного события.

Таким образом, поток можно считать ординарным, если за малый промежуток времени может произойти не более одного события (или ни одного события, вероятность чего обозначим ).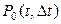

Для любого Δt очевидно справедливо:

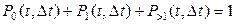, (1.2)

т.к. составляющие формулы (1.2) определяют полную группу несовместных событий.

Для ординарного потока:

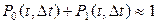, (1.3)

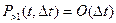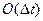потому что , где - величина, порядок малос-ти которой выше чем Δt, т. е.:

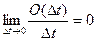. (1.4)

В качестве примера ординарного потока можно привести ситуацию на автостраде, когда машины пересекают линию «Стоп», даже при многорядном движении. Пример неординарного потока – поток пассажиров, прибывающих в лифте на данный этаж.

Стационарный поток определяется следующим образом. Для стационарного потока вероятность появления некоторого числа событий за интервал τ, зависит только от τ (длины интервала) и не зависит от расположения τ на оси t.

Регулярный поток и поток Пальма с одинаково распределёнными интервалами T_i являются стационарными потоками.

Возьмём ординарный поток. Среднее число событий, произошедших за время Δt (вычисляется по формуле математического ожидания):

.

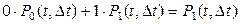Если существует предел

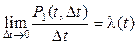, (1.5)

то 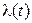называется интенсивностью ординарного потока (раз-мерность [1/t]). Для стационарного потока: 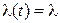- число со-бытий в единицу времени.