Генеральная и выборочная совокупность.
Всю совокупность единиц, которые подлежат обследованию называют генеральной совокупностью. Ее численность обозначается N.
Часть совокупности, которая подлежит выборочному обследованию, называют выборочной, ее численность обозначается n.
Задание выборочного наблюдения – получить правильное представление о показателях генеральной совокупности на основе изучения выборочной совокупности.
При выборочном наблюдении имеют дело с двумя категориями обобщающих показателей:
- доля (удельный вес) (в генеральной совокупности обозначается P, в выборочной – w);
- средняя величина.
Удельный вес дает характеристику совокупности по вариационному признаку и рассчитывается как отношение числа единиц совокупности, которые имеют интересующий нас признак к общему числу единиц совокупности.
Среднее значение вариационного признака во всей генеральной совокупности называется генеральной средней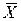 
, а среднее значение признака, который подлежит выборочному наблюдению называется выборочной средней 
.
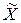В процессе статистических исследований нередко приходится ограничивать объем выборки. В статистике доказано, что даже выборки весьма малого объема (до 30 единиц), которые называют малыми выборками, позволяют получить приемлемые для анализа результаты.
Проблема малых выборок была решена в 1908г. английским статистиком У.Гассетом (псевдоним Стьюдент (студент)). Он сумел определить зависимость между величиной доверительного коэффициента t, а так же численностью малой выборки n с одной стороны, и вероятностью нахождения ошибки выборки в заданных пределах с другой стороны. Эта зависимость получила название – распределение Стьюдента.
Для определения возможных границ ошибки пользуются так называемым критерием Стьюдента, который определяется по формуле:
,
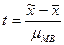где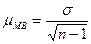 
мера случайных колебаний выборочной средней в малой выборке.
Размер рассчитывается на основе данных выборочного наблюдения по формуле:
.
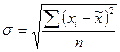Для упрощения расчетов имеются специальные таблицы значений критериев Стьюдента.
Дата добавления: 2019-04-03; просмотров: 291;