Понятие об ошибках выборки.
Ошибка выборки возникает из-за различий в вариации значений изучаемого признака у единиц выборочной и генеральной совокупности. Поскольку при соблюдении требований случайного отбора все единицы генеральной совокупности имеют равные шансы попасть в выборку, состав выборки может значительно изменяться при повторении испытаний. Соответственно будут меняться параметры выборки, и возникать ошибки выборки. Ошибки выборки неизбежны, они вытекают из сути метода. Ошибки выборки не могут быть постоянными при повторении отбора.
Вероятность появления определенной ошибки выборки находят с помощью теорем теории вероятностей. Согласно теореме Чебышева, при достаточно большом объеме выборки и ограниченной дисперсии генеральной совокупности вероятность того, что разность между выборочной средней и генеральной средней будет сколь угодно мала, близка к единице:
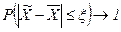при 
.
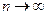А. М. Ляпунов доказал, что независимо от характера распределения генеральной совокупности при увеличении объема выборки распределение вероятностей появления того или иного значения выборочной средней приближается к нормальному распределению (центральная предельная теорема). Следовательно, вероятность отклонения выборочной средней от генеральной средней, т.е. вероятность появления заданной предельной ошибки, также подчиняется указанному закону и может быть найдена как функция от t с помощью интеграла вероятностей Лапласа:
,
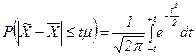где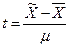 
– нормированное отклонение выборочной средней от генеральной средней.
При определении ошибки выборки речь идет о том, чтобы максимально приблизить показатели выборочной совокупности к показателям генеральной совокупности и выявить допустимые граничные отклонения этих показателей.
В процессе выборочного наблюдения возможно решить 2 задачи:
- установить пределы (границы) среднего значения признака в генеральной совокупности: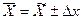 
;
- найти пределы (границы) доли альтернативного признака в генеральной совокупности: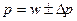 
.
Ошибка репрезентативности, или разница между выборочной и генеральной характеристикой (долей или средней), которая возникает вследствие несплошного наблюдения, в основе которого лежит случайный отбор, рассчитывается как граница вероятной ошибки (предельная ошибка выборки).
В общем виде предельная ошибка выборки определяется (на основе теоремы Ляпунова) как:
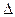= t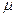 
,
где t – коэффициент доверия, зависящий от вероятности, с которой определяется предельная ошибка выборки (значения t при заданной вероятности P определяются по таблице значений, которая рассчитывается по формуле Лапласа).
Например, при P=0,683 t=1,
при P=0,954 t=2,
при P=0,997 t=3.
Вероятность, которая принимается при расчете выборочной характеристики, называется доверительной. В качестве уровня доверительной (гарантированной) вероятности принимается, обычно, 0,954 или 0,997. Тогда граница ошибки определяется величиной, удвоенной или утроенной по отношению к средней ошибке выборки .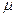
Средняя ошибка выборки определяется по формулам:
- для повторного случайного отбора
= 
;
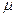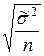– для бесповторного случайного и механического отборов
= 
;
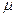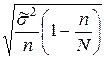где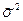
-дисперсия (для типовой выборки - средняя из внутригрупповых дисперсий; для простой случайной и механической выборок – дисперсия выборочной совокупности).
Таким образом, предельная ошибка выборки для средней рассчитывается по формулам:
- для повторного случайного отбора
;
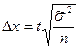– для бесповторного случайного и механического отборов
.
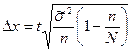Предельная ошибка выборки для доли альтернативного признака:
- при повторном отборе
,
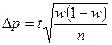- при бесповторном
,
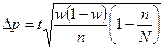где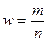 
-доля альтернативного признака;
m-численность совокупности по альтернативному признаку;
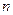- численность выборочной совокупности.
Следовательно, при выборочном наблюдении определяется не одно, точное значение обобщающей характеристики генеральной совокупности, а лишь ее доверительный интервал с заданным уровнем вероятности. И это серьезный недостаток выборочного метода статистики.
Вероятности конкретного размера ошибок подсчитать невозможно (нецелесообразно), гораздо важнее знать, что ошибка наблюдений не выйдет за определенные пределы.
Рассмотрим пример. Допустим, в результате выборочного исследования жилищных условий жителей города, осуществленного на основе случайной повторной выборки, получен такой ряд распределения.
Таблиця 9.1
Дата добавления: 2019-04-03; просмотров: 524;