Результаты выборочного исследования жилищных условий жителей города
| Общая (полезная) площадь жилья на 1 человека, м2 | До 5 | 5-10 | 10-15 | 15-20 | 20-25 | 25-30 | 30 и более |
| Число жителей |
Для определения средней ошибки выборки нам необходимо рассчитать выборочную среднюю, дисперсию исследуемого признака и стандартное среднеквадратическое отклонение.
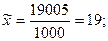
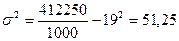 ;
;
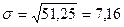 .
.
Тогда средняя ошибка выборки составит:
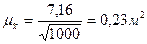 .
.
Таблиця 9.2
Расчет средней общей площади жильця на 1 человека и дисперсии
| Общая площадь жилья на 1 человека, м2 | Число жителей f | Средина интервала x | xf | х2 f |
| До 5,0 5,0-10,0 10,0-15,0 15,0-20,0 20,0-25,0 25,0-30,0 30,0 і більш | 2,5 7,5 12,5 17,5 22,5 27,5 32,5 | 20,0 712,5 2550,0 4725,0 4725,0 3575,0 2697,0 | 50,0 5343,75 31875,0 82687,5 106321,5 98312,5 87668,75 | |
| Итого | - | 19005,0 | 412250,0 |
Определим предельную ошибку выборки с вероятностью 0,954 (t=2):
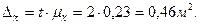
Установим границы генеральной средней:

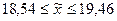 .
.
Таким образом, на основании проведеного выборочного исследования с вероятностью 0,954 можно утверждать, что средний размер общей площади жилья на 1 человека, в целом по городу находится в пределах от 18,5 до 19,5 м2.
При расчете средней ошибки бесповторной выборки не обходимо сделать поправку на бесповторность отбора:
Если допустить, что приведенные в табл. 9.1. данные являются результатом 5%-ного бесповторного отбора (т.е. генеральная совокупность включает 20000 единиц), то средняя ошибка выборки буде травна:
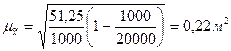 .
.
Определим границы доли лиц, обеспеченность жильем которых менее 10 м2.
В соответствии с результатами исследования, численность таких лиц составила 103 человека. Определим выборочную долю и дисперсию:
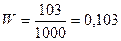 ,
,
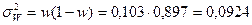 .
.
Рассчитаем среднюю ошибку выборки:
 .
.
Предельная ошибка выборки с заданной вероятностью составит:



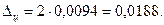

Определим границы генеральной доли:
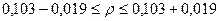 ,
,  или
или 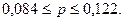
Таким образом, с вероятностью 0,954 можно утверждать, что доля лиц имеющих площадь жилья менее 10 м2 на человека , в целом по городу находится в пределах от 8,4 до 12,2%.
Дата добавления: 2019-04-03; просмотров: 848;
