Генеральная и выборочная совокупности

Пусть требуется изучить данную совокупность объектов относительно некоторого признака. Например, рассматривая работу диспетчера (продавца, парикмахера,...), можно исследовать: его загруженность, тип клиентов, скорость обслуживания, моменты поступления заявок и т.д. Каждый такой признак (и их комбинации) образует случайную величину, над которой производят наблюдения.

Совокупность всех подлежащих изучению объектов или возможных результатов всех мыслимых наблюдений, производимых в неизменных условиях над одним объектом, называется генеральной совокупностью.

Более строго: генеральная совокупность - это случайная величина 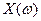, заданная на пространстве элементарных событий Ω с выделенным в нем классом S подмножеств событий, для которых указаны их вероятности.

Зачастую проводить сплошное обследование, когда изучаются все объекты (например - перепись населения), трудно или дорого, экономически нецелесообразно, а иногда невозможно. В этих случаях наилучшим способом обследования является выборочное наблюдение: выбирают из генеральной совокупности часть ее объектов («выборку») и подвергают их изучению.

Выборочной совокупностью (выборкой) называется совокупность объектов, отобранных случайным образом из генеральной совокупности.

Более строго: выборка - это последовательность 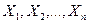независимых одинаково распределенных случайных величин, распределение каждой из которых совпадает с распределением генеральной случайной величины.

Число объектов (наблюдений) в совокупности называется ее объемом.

Конкретные значения выборки, полученные в результате наблюдений (испытаний), называют реализацией выборки и обозначают строчными буквами .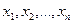

Метод статистического исследования, состоящий в том, что на основе изучения выборочной совокупности делается заключение о всей генеральной совокупности, называется выборочным.

Для получения хороших оценок характеристик генеральной совокупности необходимо, чтобы выборка была репрезентативной (или представительной), т.е. достаточно полно представлять изучаемые признаки генеральной совокупности. Условием обеспечения репрезентативности выборки является, согласно закону больших чисел, соблюдение случайности отбора, т.е. все объекты генеральной совокупности должны иметь равные вероятности попасть в выборку.

Различают выборки с возвращением (повторные) и без возвращения (бесповторные). В первом случае отобранный объект возвращается в генеральную совокупность перед извлечением следующего; во втором - не возвращается. На практике чаще используется бесповторная выборка.

Заметим, если объем выборки значительно меньше объема генеральной совокупности, различие между повторной и бесповторной выборками очень мало, его можно не учитывать.

В зависимости от конкретных условий для обеспечения репрезентативности применяют различные способы отбора:

- простой, при котором из генеральной совокупности извлекают по одному объекту;

- типический, при котором генеральную совокупность делят на «типические» части и отбор осуществляется из каждой части (например, мнение о референдуме спросить у случайно отобранных людей, разделенных по признаку пола, возраста,...);

- механический, при котором отбор производится через определенный интервал (например, мнение спросить у каждого шестидесятого...);

- серийный, при котором объекты из генеральной совокупности отбираются «сериями», которые должны исследоваться при помощи сплошного обследования.

На практике пользуются сочетанием вышеупомянутых способов отбора.