Корреляционно-регрессионный анализ в макроэкономическом прогнозировании
Большинство явлений и процессов в экономике находятся в постоянной взаимной и объективной связи. Исследование зависимостей и взаимосвязей между объективно существующими явлениями и процессами играет большую роль в экономике. Оно даёт возможность глубже понять сложный механизм причинно-следственных отношений между явлениями. Для исследования интенсивности, вида и формы зависимостей широко применяется корреляционно-регрессионный анализ, который является методическим инструментарием при решении задач прогнозирования и планирования.
Различают два вида зависимостей между экономическими явлениями и процессами – функциональную и стохастическую (вероятностную, статистическую).
В случае функциональной зависимости имеется однозначное отображение множества А на множество В. Множество А называют областью определения функции, в множество В – множеством значений функции.
Функциональная зависимость встречается редко. В большинстве случаев функция (Y) или аргумент (Х) – случайные величины. Х и Y подвержены действию различных случайных факторов, среди которых могут быть факторы, общие для двух случайных величин.
Статистическойназывается зависимостьмежду случайными величинами, при которой изменение одной из величин влечёт за собой изменение закона распределения другой величины. В этом случае говорят о корреляционной зависимости. В экономике приходится иметь дело со многими явлениями, имеющими вероятностный характер. Например, к числу случайных величин можно отнести стоимость продукции, доходы бюджетов и др.
Односторонняя вероятностная зависимость между случайными величинами есть регрессия. Она устанавливает соответствие между этими величинами.
Односторонняя стохастическая зависимость выражается с помощью функции, которая называется регрессией. В общем виде такая зависимость может быть представлена следующим образом:
Yit =f (Xkt, et ),
где Yit – i-я зависимая переменная в момент времени t, Xkt – k-я независимая переменная (фактор) в момент времени t, et – ошибка наблюдения в момент времени t.
Уравнение регрессии характеризует взаимосвязь переменных X и Y в том смысле, что показывает, как изменяется величина Y в зависимости от изменения величины Х.
Перечислим различные виды регрессии.
1. Регрессия относительно числа переменных:
- простая регрессия – регрессия между двумя переменными;
- множественная регрессия – регрессия между зависимой переменной Y и несколькими независимыми переменными Х1,Х2…Хm.
2. Регрессия относительно формы зависимости:
- линейная регрессия, выражаемая линейной функцией;
- нелинейная регрессия, выражаемая нелинейной функцией.
3. В зависимости от характера регрессии различают:
-положительную регрессию. Она имеет место, если с увеличением (уменьшением) независимой переменной значения зависимой переменной также соответственно увеличиваются (уменьшаются);
- отрицательную регрессию. В этом случае с увеличением или уменьшением независимой переменной зависимая переменная уменьшается или увеличивается.
Регрессия тесно связана с корреляцией. Корреляция в широком смысле слова означает связь, соотношение между объективно существующими явлениями. Связи между явлениями могут быть различны по силе. При измерении тесноты связи говорят о корреляции в узком смысле слова.
Понятия «корреляция» и «регрессия» тесно связаны между собой. В корреляционном анализе оценивается сила связи, а в регрессионном анализе исследуется её форма. Корреляция в широком смысле объединяет корреляцию в узком смысле и регрессию.
Исследование корреляционных связей называют корреляционным анализом, а исследование односторонних стохастических зависимостей – регрессионным анализом. Корреляционный и регрессионный анализ имеют свои задачи.
К задачам корреляционного анализа относятся следующие:
1.Измерение степени связности(тесноты, силы) двух и более явлений.
2.Отбор факторов, оказывающих наиболее существенное влияние на результирующий признак, на основании измерения тесноты связи между явлениями.
3.Обнаружение неизвестных причинных связей. Корреляция непосредственно не выявляет причинных связей между явлениями, но устанавливает степень необходимости этих связей и достоверность суждений об их наличии. Причинный характер связей выясняется с помощью логически-профессиональных суждений, раскрывающих механизм связей.
Перечислим задачи регрессионного анализа:
1. Установление формы зависимости (линейная, нелинейная, положительная или отрицательная и т.д.).
2. Определение функции регрессии и установление влияния факторов на зависимую переменную. Важно не только определить форму регрессии, указать общую тенденцию изменения зависимой переменной, но и выяснить, каково было бы действие на зависимую переменную главных факторов, если прочие не изменились и если бы были исключены случайны элементы. Для этого определяют функцию регрессии в виде математического уравнения того или иного типа.
Построение корреляционно-регрессионной модели осуществляется в несколько этапов:
1. Постановка задачи.
2. Сбор статистических данных.
3. Корреляционно-регрессионный анализ данных.
4. Прогнозирование на основе полученной зависимости.
Постановка задачи.На первом этапе даётся постановка задачи. Например, определить численность занятых в стране в зависимости от произведённого валового продукта; зависимость затрат от количества работников на предприятии и т.д. На этом этапе также считается, что связь между независимыми показателями и результирующим показателем (зависимым) может существовать и характеризуется функцией Y=f(Xn).
Статистические данные набираются на основе первичных документов и отчётных данных. Некоторые показатели могут быть получены только после предварительной обработки полученной информации. При сборе данных необходимо определить количество выборочных наблюдений или выборочную совокупность, т.е. часть наблюдений, отобранных для дальнейшего исследования.
Объём выборочных наблюдений (Кв) определяется по формуле предельной ошибки случайной бесповторной выборки:
Кв= 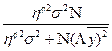 ,
,
где N – величина генеральной совокупности, т.е. величина всей совокупности наблюдений, отображаемых результативных признаков и факторов;
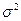 – дисперсия значений признака в генеральной совокупности;
– дисперсия значений признака в генеральной совокупности;
D 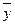 – предельная ошибка случайной бесповторной выборки;
– предельная ошибка случайной бесповторной выборки;
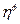 – коэффициент доверия.
– коэффициент доверия.
Дисперсия 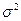 является характеристикой рассеивания случайных величин, т.е. их отклонения от средней величины. Квадратный корень из дисперсии – среднее квадратическое отклонение определяется по формуле
является характеристикой рассеивания случайных величин, т.е. их отклонения от средней величины. Квадратный корень из дисперсии – среднее квадратическое отклонение определяется по формуле
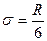 ,
,
где R – есть разница между максимальным и минимальным значением признака (фактора). Она устанавливается на основе анализа данных.
Размеры предельной ошибки по абсолютной величине D 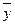 задаются в зависимости от требований точности к полученным результатам. Например, если признак исчисляется в сотнях рублей, то предельная ошибка может быть установлена в рублях; если в днях, то в части дня (0,1дня).
задаются в зависимости от требований точности к полученным результатам. Например, если признак исчисляется в сотнях рублей, то предельная ошибка может быть установлена в рублях; если в днях, то в части дня (0,1дня).
После сбора данных осуществляется их регрессионный анализ, который включает три этапа:
1) определение вида функции (уравнения регрессии);
2) определение тесноты связи между переменными;
3) установление числового значения параметров уравнения регрессии.
На первом этапе определяется форма связи исследуемых показателей или уравнение регрессии. Функциональная зависимость определяется следующим образом: предположим, что линия регрессии переменной, которую мы обозначим 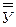 , от переменной Х имеет вид:
, от переменной Х имеет вид: 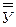 = а0 + а1Х+
= а0 + а1Х+ 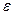 – это простейший вид зависимости между двумя показателями – линейная зависимость. Здесь
– это простейший вид зависимости между двумя показателями – линейная зависимость. Здесь 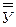 – результативный показатель, а0 и а1 – постоянные коэффициенты; Х – фактор,
– результативный показатель, а0 и а1 – постоянные коэффициенты; Х – фактор, 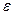 – добавочный коэффициент, при учёте которого
– добавочный коэффициент, при учёте которого 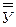 никогда не может попасть на линию регрессии, т.е.
никогда не может попасть на линию регрессии, т.е. 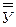
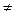 Х.
Х.
Это уравнение можно использовать как предсказывающее уравнение, подстановка в него значения Х позволяет предсказать истинное среднее значение У для этого Х.
Проверка линейной зависимости может быть проведена путём сопоставления по собранным данным вариации результативного и факторного признаков. Любую форму зависимости можно проверить графическим путём, отмечая каждое наблюдение точкой в прямоугольной системе координат. По оси ординат откладываются значения У, а по оси абсцисс – значение Х.
Вторым этапом проверяется теснота связи выбранных показателей, т.е. насколько полно выбраны факторные признаки, как велико влияние неучтённых факторов. Поэтому оценка параметров регрессии обычно сопровождается расчётом такой дополнительной характеристики, как коэффициент корреляции, который представляет собой эмпирическую меру линейной зависимости между Х и Y:
ry,x= ( 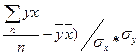 ,
,
где 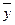 - среднеарифметическое значение результативных признаков;
- среднеарифметическое значение результативных признаков; 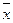 – среднеарифметическое значение факторов; n – количество выборочных наблюдений;
– среднеарифметическое значение факторов; n – количество выборочных наблюдений; 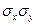 – среднее квадратическое отклонение результирующего и факторного признаков.
– среднее квадратическое отклонение результирующего и факторного признаков.
Среднее квадратическое отклонение фактора 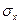 рассчитывается по формуле
рассчитывается по формуле
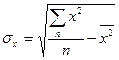 .
.
Среднее квадратическое отклонение значений результирующего признака рассчитывается по формуле
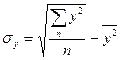 .
.
Величина коэффициента корреляции лежит между (-1;1). Чем выше значение коэффициента корреляции, тем теснее связь между переменными и тем точнее будет прогноз, произведённый на основе полученного уравнения регрессии. Если коэффициент корреляции равен +1, то связь между показателями выражается в прямой зависимости, т.е. при увеличении одного показателя увеличивается и второй, и наоборот. Если же коэффициент корреляции равен –1, то связь между двумя показателями выражается в обратной зависимости, т.е. при увеличении одного показателя другой уменьшается, и наоборот.
О тесноте связи можно судить по значению коэффициента корреляции, используя шкалу Чеддока:
| Показатель тесноты связи | 0,1– 0,3 | 0,3 – 0,5 | 0,5 – 0,7 | 0,7 – 0,9 | 0,9 – 0,99 |
| Характеристика силы связи | слабая | умеренная | заметная | высокая | весьма высокая |
Завершающим этапом является определение численных значений постоянных коэффициентов уравнения регрессии (а0 и а1). Эти коэффициенты находятся в результате решения системы уравнений. Систему можно получить с помощью метода наименьших квадратов. Метод наименьших квадратов позволяет из бесчисленного множества прямых линий на плоскости выбрать одну, наилучшим образом соответствующую исходным данным.
Этот метод обладает определёнными свойствами: пусть мы имеем множество из n наблюдений (Х1,Y1), (Х2,Y2)…(Хn, Yn). Тогда уравнение 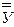 = а0 + а1Х+
= а0 + а1Х+ 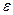 можно записать в виде:
можно записать в виде:
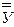 i = а0 + а1Хi+
i = а0 + а1Хi+ 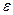 i, где i=1,2…n.
i, где i=1,2…n.
Следовательно, сумма квадратов отклонений фактических значений от расчётных равна:
S= 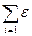 i2=
i2= 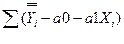 2.
2.
Будем подбирать значения оценок а0 и а1 так, чтобы их подстановка в уравнение давало наименьшее значение S, т.е. 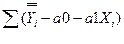 2= S
2= S 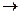 min
min
Определим а0 и а1, дифференцируя уравнение S= 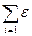 i2=
i2= 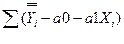 2 сначала по а0, затем по а1, и приравняем результаты к нулю. Тогда получим:
2 сначала по а0, затем по а1, и приравняем результаты к нулю. Тогда получим:
 na0 + a1
na0 + a1 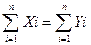
a0 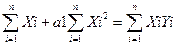
Эти уравнения представляют собой систему нормальных уравнений. Отсюда находим коэффициенты регрессионной функции:
а1= 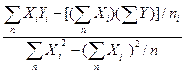 =
= 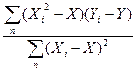 .
.
Решение системы уравнений относительно а0: а0=Y-a1X. С помощью подстановки этого уравнения в уравнение 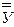 i = а0 + а1Хi+
i = а0 + а1Хi+ 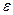 i получим оцениваемое уравнение регрессии Yi= Y+a1X.
i получим оцениваемое уравнение регрессии Yi= Y+a1X.
Для практического использования регрессионных моделей важно установить, насколько точно могут быть рассчитаны значения исследуемого показателя по заданным значениям факторов. Для оценки точности уравнений регрессии на практике используют ряд показателей: коэффициент множественной корреляции (детерминации), критерий Фишера, остаточная дисперсия, критерий Стьюдента и др.[2]
Следует отметить, регрессионные приёмы анализа и прогнозирования не вскрывают специфические причины изучаемых явлений, а только дают возможность определить количественную величину связей между ними. Причины могут быть вскрыты только при тщательном изучении технической, технологической и организационной сторон процесса производства и экономических отношений.
Ведущим направлением корреляционного анализа в экономике является исследование зависимостей в сфере производства как на макро- так и на микроуровне. Результат процесса производства складывается под влиянием многочисленных и разнообразных факторов. Качественный анализ позволяет в каждом конкретном случае установить, какие именно факторы влияют на результат производства. Цель построения производственных функций – количественно оценить, измерить характер и степень такого влияния.
Одним из наиболее важных направлений использования аппарата производственных функций является анализ эффективности использования ресурсов производства. С помощью производственных функций можно исследовать эффективность трудовых ресурсов, производственных фондов, природных и других ресурсов не изолированно, а в их взаимодействии, выявлять границы взаимозаменяемости ресурсов и наиболее рациональные их пропорции с точки зрения конечного результат производства.
Существенную роль играют производственные функции как инструмент прогнозирования конечных результатов производственной деятельности. Аппарат производственных функций используют при проведении прогнозных расчётов на долгосрочную перспективу, когда необходимо исследовать производственный потенциал страны и эффективность использования факторов в процессе производства.
Производственная функция – это экономико-математическая зависимость, связывающая результаты производственной деятельности и обусловливающие эти результаты ресурсы (факторы производства):
Yt = f(Rst),
где t – индекс временного интервала; s – индекс вида ресурсов (технико-экономических факторов); Y – результат производственной деятельности; R – вид ресурса.
Учесть влияние сразу всех факторов на результат хозяйственной деятельности невозможно, т.к. воздействие одних из них не подлежит количественному анализу, влияние других же очень несущественно. Производственная функция включает лишь некоторые из них, наиболее важные, которые оказывают решающее воздействие на результирующий показатель.
Из-за наличия неучтённых факторов и неоднозначного действия учтённых производственная функция является функцией лишь в статистическом смысле: описываемая ею математическая зависимость проявляется только в общем и среднем в массе наблюдений. Соответственно и аппаратом исследования производственных функций служат методы математической статистики.
По своему содержанию производственные функции охватывают всевозможные зависимости в сфере производства на различных уровнях – предприятие, группа предприятий, отрасль, регион, национальная экономика. Различают макроэкономические и микроэкономические производственные функции. С помощью макроэкономических производственных функций изучают агрегированные характеристики процесса производства на уровне отраслей, групп отраслей, национальной экономики в целом. К микроэкономическим производственным функциям относятся функции, которые описывают взаимосвязь результата производства и факторов на уровне предприятий, группы предприятий.
Производственные функции подразделяются на статические и динамические. В статических не учитывается время как фактор, изменяющий основные характеристики изучаемой зависимости. Динамические производственные функции включают фактор времени; время может фигурировать в них как самостоятельная величина, влияющая на результативный показатель; параметры и показатели – факторы также могут рассматриваться как функции времени.
Наиболее распространёнными и в то же время самыми простыми видами производственных функций, которые широко применяются в социально-экономическом прогнозировании, являются:
· линейная производственная функция Y = aK + bL +g;
· производственная функция Кобба-Дугласа Y = AKaLb,
где Y – объём выпуска продукции; К – объём производственных фондов; L – численность занятых; А, a, b, g – параметры производственных функций, конкретные числовые значения, которые определяются c помощью корреляционных методов.
Рассмотрим пример прогноза на основе использования корреляционно-регрессионного анализа. Оценить зависимость между среднедушевыми доходами населения и потреблением мяса и мясопродуктов на душу населения в регионе за 11 лет (таблица 3.4). Сделать прогноз потребления мяса и мясопродуктов на душу населения при условии, что среднедушевые доходы в следующем году увеличатся на 10%.
Таблица 3.4 – Исходные данные по региону
| Год | Среднедушевые денежные доходы населения (в месяц в руб., до пятого г. – тыс. руб.) | Потребление мяса и мясопродуктов на душу населения в год, кг |
| 0,248 | ||
Рассмотрим решение задачи средствами Excel.
1. Заносим статистические данные на лист Excel.
2. Оценим тесноту связи между среднедушевыми доходами населения и потреблением мяса и мясопродуктов на душу населения. Для этого выберем АНАЛИЗ ДАННЫХ ® КОРРЕЛЯЦИЯ ® ОК.
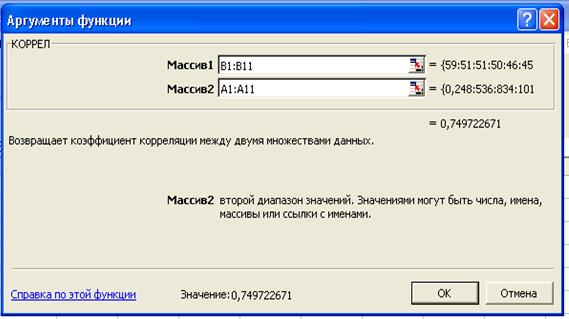
В открывшемся диалоговом окне КОРРЕЛЯЦИЯ зададим несколько параметров: в поле Массив 1 укажем диапазон ячеек В1:В11, в поле Массив 2 – диапазон ячеек А1:А11.После того как все необходимые параметры заданы, щёлкните по кнопке ОК – Excel выводит на лист коэффициент корреляции. Для данных исходных данных он равен 0,749, это означает, что связь между показателями высокая. Следовательно, можно перейти к регрессионному анализу.
3. Составим уравнение регрессионной зависимости. Для этого выберем АНАЛИЗ ДАННЫХ®РЕГРЕССИЯ®ОК. В открывшемся диалоговом окне РЕГРЕССИЯ зададим несколько параметров:
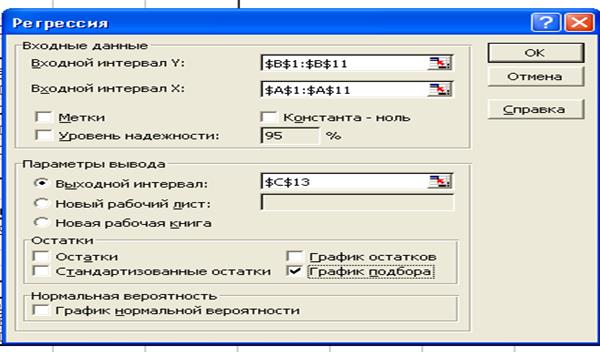
· в поле Входной интервал Y укажем диапазон с входными данными В1:В11;
· в поле Входной интервал X укажем диапазон с входными данными А1:А11;
· флажок Метки устанавливают, если первая строка исходного диапазона содержит название полей – в нашем случае – нет.
· флажок Константа – ноль устанавливается, если требуется, чтобы линия регрессии проходила через начало координат – в нашем случае – нет;
· флажок Уровень надёжности устанавливают с целью изменить уровень значимости a (Excel автоматически задаёт надёжность g=0,95, что соответствует уровню значимости a=1 – g=0,05). В случае a¹0,05 установите флажок и в соседнем поле введите надёжность 1 – a. В нашем случае этого не требуется;
· с помощью переключателя Параметры вывода, определим, куда должны быть помещены выходные данные – установим переключатель в позицию Выходной интервал, в соответствующем поле укажем ячейку C13.
· флажок Остатки устанавливают, если требуется получить разность между фактическими и теоретическими значениями Y – не устанавливаем флажок;
· флажок График остатков устанавливают, если требуется получить диаграмму остатков для каждого значения X – не устанавливаем флажок;
· флажок Стандартные остатки устанавливают, если требуется получить нормальные остатки (каждый из остатков делится на стандартное отклонение остатков) – не устанавливаем флажок;
· флажок График подбора устанавливают, если требуется получить точечную диаграмму входных значений Y и значений Y, вычисленных по уравнению регрессии относительно переменной X – устанавливаем флажок;
· флажок График нормальной вероятности устанавливают, если требуется получить график нормального распределения персентиля выборки и исходных значений Y – не устанавливаем флажок.
После того как все необходимые параметры заданы, щёлкаем по кнопке ОК – Excel выводит параметры уравнения регрессии.
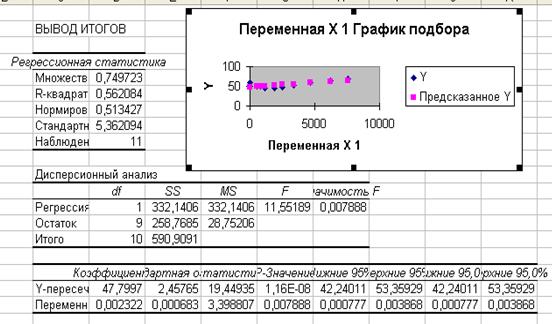
4. Для того чтобы уравнение появилось на диаграмме, необходимо правой кнопкой мыши нажать на одно из значений графика Прогноза. Далее в диалоговом окне выбрать Добавить линию тренда.
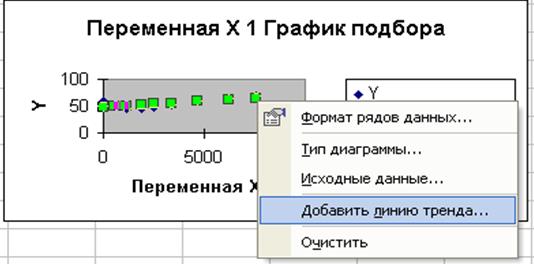
5. В диалоговом окне Линия тренда выберите тип предполагаемой зависимости, например, предположим, что зависимость линейная. Далее выберите команду Параметры, в появившемся диалоговом окне отметьте флажок на команде Показать уравнение на диаграмме.
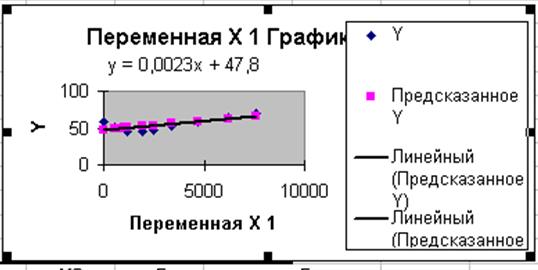
С помощью полученного уравнения регрессии У= 0,0023х + 47,8 получим прогнозное значение У = 0,0023*7552*1,1 + 47,8 = 66,9 кг – прогнозное значение потребления мяса и мясопродуктов на душу населения в год в регионе, при условии, что среднедушевые доходы увеличатся в следующем году на 10%.
Дата добавления: 2017-02-20; просмотров: 4253;
