Понятие рядов распределения
Отдельный вид группировок в статистике - ряды распределения, которые являются наипростейшим способом обобщения статистических данных.
Ряд распределения – это группировка, которая характеризует состав (структуру) явления в данный период времени.
В зависимости от того, какой признак (количественный или качественный) положен в основу группировки, ряды распределения бывают:
- атрибутивные (качественные) (например, распределение населения по возрасту, занятости, национальности, профессии и т.д.);
- вариационные (количественные).
Вариационные ряды распределения бывают дискретными и интервальными.
Дискретный ряд – это ряд, в котором варианты (отдельные значения группировочного признака) выражены целыми числами (табл. 6.1.).
Таблица 6.1.
Распределение работников по тарифным разрядам
| Тарифный разряд | Количество работников, чел. |
| Итого |
Интервальный ряд распределения – ряд, в котором значения признака заданы в виде интервалов (табл.6.2.).
Таблица 6.2.
Распределение коммерческих банков по величине капитала
| Размер капитала, млн.р. | Количество банков, ед. |
| 3-6 | |
| 6-9 | |
| 9-12 | |
| Итого |
Ряд распределения состоит из двух элементов: вариант и частот.
Варианты– числовые значения количественного признака в группировке (они могут быть абсолютными, относительными, отрицательные, положительные) (первая графа таблицы).
Частоты – числа, которые показывают, сколько раз повторяются отдельные значения вариант (выражаются в виде коэффициентов или процентов (доля)). Накопленную частоту называют кумулятивной.
Ранжированным рядом распределения называют ряд, в котором значения признака располагаются в возрастающем (снижающемся) порядке и расчет ведется по группам.
Графически дискретный ряд изображается в виде полигона, а вариационный ряд с равными интервалами – в виде гистограммы. Ряд распределения с неравными интервалами также представляется в виде гистограммы, которая строится на основе тесноты распределения.
Теснота распределения – количество элементов совокупности, которое приходится на единицу ширины интервала группировочного признака. Например, по количеству ученических мест 400 школ области находятся в интервале от 800-1000. Тогда теснота распределения составляет 400/(1000-800) =2.
2. Характеристики центра распределения: мода и медиана
К характеристикам центра распределения, кроме обобщающих характеристик совокупности (средней арифметической, средней гармонической), принадлежат вспомогательные описательные характеристики распределения вариационного признака, которые называют структурными средними – мода и медиана.
Мода и медиана – это типовые характеристики в тех случаях, когда совокупности однородные и значительные по численности.
Мода – это величина признака (варианта), которая чаще всего встречается в данной совокупности.
Мода используется в тех случаях, когда нужно охарактеризовать величину признака, которая наиболее часто повторяется. Например, наиболее распространенный размер заработной платы на предприятии, цены на рынке, по которой было продано наибольшее количество товара, размер обуви, который имеет наибольший спрос среди населения.
Способ расчета моды зависит от вида статистического ряда. В атрибутивных и дискретных рядах модой является варианта, которая имеет наибольшую частоту. Например, рассмотрим распределение семей по числу детей (табл. 6.3.)
Таблица 6.3.
Распределение семей по числу детей
| Группы семей по числу детей | Число семей |
| Всего |
Модой будет группа семей, которая имеет двух детей, т.к. этому значению варианты соответствует наибольшее число семей (75).
Если в распределениях все варианты встречаются одинаково часто, они все считаются модальными. Если не одна, а две варианты имеют наибольшие частоты распределение будет бимодальным.
В интервальном ряду для определения моды вначале находят модальный интервал исследуемого ряда (интервал с наибольшей частотой). Например, рассмотрим распределение работников по размеру заработной платы (табл. 6.4.).
Таблица 6.4.
Распределение работников по размеру заработной платы
| Группы работников по размеру заработной платы, р. | Количество работников |
| 1300-1400 | |
| 1400-1500 | |
| 1500-1600 | |
| 1600-1700 | |
| 1700-1800 | |
| 1800-1900 | |
| Итого |
Наибольшая частота (f) соответствует интервалу, где варианта находится в границах 1700-1800. Это и будет модальный интервал.
Для расчета значения модальной величины признака, который находится в этом интервале используют зависимость:
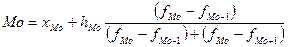
где 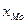 - нижняя граница модального интервала (в нашем случае 1700);
- нижняя граница модального интервала (в нашем случае 1700); 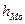 - величина модального интервала (100);
- величина модального интервала (100); 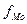 - частота, соответствующая модальному интервалу (180);
- частота, соответствующая модальному интервалу (180); 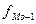 - частота, предшествующая модальному интервалу (115);
- частота, предшествующая модальному интервалу (115); 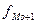 -частота интервала, следующего за модальным (45).
-частота интервала, следующего за модальным (45).
В нашем случае (табл. 6.4):
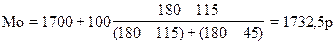
Медианойназывается варианта, которая находится в середине упорядоченного вариационного ряда. Медиана делит ряд на две, равные по численности, части.
Для ранжированного ряда с нечетным числом членов медианой является варианта, расположенная в центре ряда. Для ранжированного ряда с четным числом членов медианой будет средняя арифметическая из двух смежных вариант:
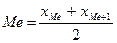 .
.
В интервальном вариационном ряду порядок нахождения медианы следующий:
1. Располагаем индивидуальные значения признака ранжировано.
2. Определяем для данного ранжированного ряда накопленные (кумулятивные) частоты (путем постепенного добавления частот, начиная с интервала, который имеет наименьшее значение признака).
3. По данным о накопленных частотах находим медианный интервал (кумулятивная частота котрого равна или превышает половину суммы частот).
4. Определяем медиану по формуле:
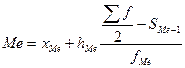
де 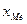 - нижняя граница медианного интервала;
- нижняя граница медианного интервала; 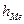 - размер медианного интервала;
- размер медианного интервала; 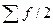 - полусумма частот ряда;
- полусумма частот ряда; 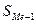 - сумма накопленных частот, предшествующих медианному интервалу;
- сумма накопленных частот, предшествующих медианному интервалу; 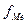 - частота медианного интервала.
- частота медианного интервала.
Рассчитаем медиану для нашего случая (табл. 6.4):
Таблица 6.5.
Расчет медианы в интервальном ряду
| Группы работников по размеру заработной платы, р. | Количество работников | Кумулятивная частота |
| 1300-1400 | ||
| 1400-1500 | ||
| 1500-1600 | ||
| 1600-1700 | ||
| 1700-1800 | ||
| 1800-1900 | ||
| Итого | - |
Половина суммы частот составляет 250 (500/2). Таким образом, медианным будет інтервал со значеним заработной платы 1600-1700. Для предыдущего интервала сумма накопленнях частот составляет 160. Значит медиана будет равна:
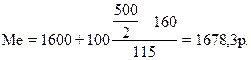
Дополнительно к медиане для характеристики вариационного ряда рссчитываются квартили (делят ряд по сумне частот на 4 равные части) и децили (делят ряд по сумне частот на 10 равных частей).
Дата добавления: 2019-04-03; просмотров: 1228;
