Двухфакторный дисперсионный анализ
Рассматривается задача оценки влияния двух одновременно действующих факторов. Допустим, что проводятся измерения различными измерительными средствами и различными операторами. Требуется оценить, обуславливается ли рассеяние полученных средних значений измерений в группах различием между измерительными средствами или различием между операторами, проводившими измерения.
Основная идея дисперсионного анализа в данном случае заключается в разложении суммы квадратов отклонений общего среднего на компоненты, отвечающие предполагаемым факторам изменчивости [7].
Предположим, что имеем два фактора А и В, по которым мы можем расклассифицировать данные наблюдения. Пусть по фактору А все наблюдения делятся на r групп А1, А2, ..Аr, по признаку В – В1, В2, В3,…Вυ. Весь материал разбивается на rυ групп. Ограничимся случаем, когда в каждой группе одно наблюдение, тогда всего наблюдений равно N= rυ. Через xij обозначим наблюдение, попавшее в группу Аi по фактору А и в группу Вj по фактору В (табл. 3). Вычислим среднее значение измерений в группах и общее среднее:
| B |
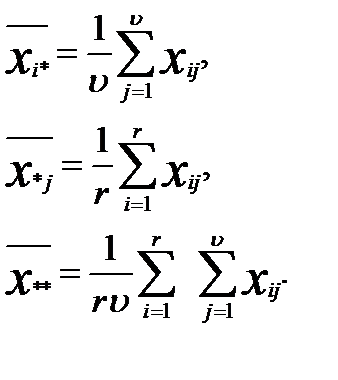
Таблица 3 - Результаты наблюдений над факторами А и В
| |||||
| B1 | B2 | Bυ | |||
| A1 | X11 | X12 | X1υ | 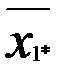
| |
| A2 | X21 | X22 | X2υ | 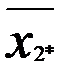
| |
| Ar | Xr1 | Xr2 | Xrυ | 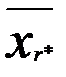
| |
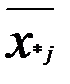
| 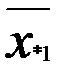
| 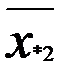
| 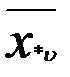
| 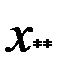
|
Из основного тождества дисперсионного анализа можно записать:
Q=Q1+Q2 +Q3,
где Q1 - сумма квадратов разностей между строками; Q2 - сумма квадратов разностей между колонками таблицы; Q3 - остаточная сумма квадратов.
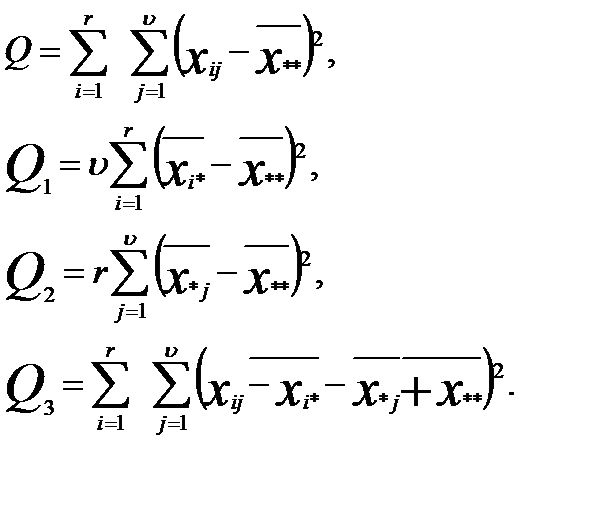
Предполагаем, что величины xij нормально распределены по закону N(x; υ; σ), где σ2 – общий неизвестный параметр дисперсии. Данные таблицы используем для проверки гипотезы о равенстве центров υij. При этой гипотезе отношения:
Q/ σ2, Q1/ σ2, Q2/ σ2, Q3/ σ2
распределены по закону χ2 с (rυ-1), (r-1), (υ-1), (r-1)(υ-1) степенями свободы соответственно, поэтому Q, Q1, Q2 ,Q3 могут быть использованы для оценки σ2.
Эта оценка может быть проверена с помощью несмещенных характеристик:
s2=Q/(rυ-1),
s12=Q1/(r-1),
s22=Q2/(υ-1),
s32=Q3/{(r-1) (υ-1)}.
Оценка параметра σ2 с помощью указанных характеристик остается в силе и в том случае, когда гипотеза о равенстве центров не верна, лишь бы равенство параметра σ2 имело место во всех наблюдениях.
Для проверки степени значимости расхождений, обнаруженных в средних по строкам и по колонкам, вычисляются критерии:
FA= s12/ s32,
FB= s22/ s32.
Расчетные значения критериев сравниваются с табличными значениями. Для уровня значимости 0,05, числа степеней свободы (r-1), {(r-1) (υ-1)} для первого отношения и числа степеней свободы (υ-1), {(r-1) (υ-1)} для второго отношения определяются квантили распределения Фишера Fтаб.А, Fтаб.В.
Если выборочные значения статистики окажутся больше критического, нулевая гипотеза отвергается и принимается альтернативная: влияние фактора А и (или) В на результативный признак существенно.
Общая схема двухфакторного дисперсионного анализа может быть представлена в виде таблицы 4.
Таблица 4 - Схема двухфакторного дисперсионного анализа
| Компоненте дисперсии | Сумма квадратов | Число степеней свободы | Оценка дисперсии |
| Между средними по строкам | Q1 | (r-1) | s12 |
| Между средними по столбцам | Q2 | (υ-1) | s22 |
| Остаточная | Q3 | {(r-1) (υ-1)}. | s32 |
| Полная (общая) | Q | (rυ-1), | s2 |
Пример 2. Для выявления меры влияния температурного режима отжига и толщины вырабатываемого стекла на отходы, используется двухфакторный дисперсионный анализ. С помощью анализа оценивали обуславливаемость рассеивания значений отходов отжига и средних значений в группах различием между толщинами вырабатываемой ленты стекла или различием температурного режима отжига. Идея дисперсионного анализа в данном случае заключается в разложении суммы квадратов отклонений общего среднего отходов на компоненты, отвечающие предполагаемым факторам изменчивости (толщины ленты стекла и температурного режима отжига). Проведена классификация анализируемых данных по двум факторам. По фактору толщины вырабатываемого стекла, наблюдения делились на четыре группы: 2-2,75; 2,75-3,5; 3,5-4.25 и 4,25-5 мм. По фактору режима отжига – на восемь групп с различным сочетанием температуры ленты стекла на выходе флоат-ванны θout, температуры в зоне D печи отжига и интенсивности охлаждения a1. Каждая составляющая режима отжига разделена на два типа – на высокие (+) и низкие значения (-) показателей по отношению к медианному значению, что обеспечивает одинаковую частность данных при расчетах. При выбранном разбиении факторов вся анализируемая выборка разбивается на 4*8=32 группы. Результаты измерений отходов стекла, распределенные по группам, сведены в таблицу 5.
Таблица 5 - Результаты разбиения отходов стекла в % по группам
| Толщина стекла | Режим отжига | |||||||||||||
| ++ + | + + - | + - + | + - - | - + + | - + - | - - + | - - - | |||||||
| 2-2,75 | - | - | - | - | 8,73; 3,38 | 6,33;7,32;6,34;5,5;8,07;5,06 | - | 6,41; 5,24 | ||||||
| 2,75-3,5 | - | 3,41; 3,54 | 3,65; 3,74 | - | 6,55 | 3,93 | - | 6,48 | ||||||
| 3,5-4,25 | 3,89 | - | 3,81;3,89;3,86;3,91; 5,07 | 3,86; 3,9 | - | - | - | - | ||||||
| 4,25-5 | - | - | 5,28 | 2,92 | - | - | 4,26 | - | ||||||
Примечание: Кодированные обозначения режимов отжига в группах записаны в следующей последовательности: температура ленты стекла на выходе флоат-ванны θout, температура в зоне D печи отжига, интенсивность охлаждения стекла в печи отжига a1.
Результаты дисперсионного анализа влияния на рассеивание отходов отжига толщины вырабатываемого стекла и режима отжига приведены в таблице 6.
Таблица 6 - Дисперсионный анализ влияния на рассеивание отходов отжига
толщины вырабатываемого стекла и режима отжига
| Компоненты дисперсии | Сумма квадратов | Число степеней свободы | Средний квадрат |
| Между толщинами стекла Между режимами отжига Остаточная Общая | 26,04 34,19 4,52 64,75 | 8,68 4,88 0,21 2,089 |
Проверим степень значимости расхождений, обнаруженных в средних по толщинам вырабатываемого стекла (строкам табл.5) при помощи F-критерия:
Fт=8,68/0,21=40,3
и для среднего квадрата между режимами отжига:
Fр=4,88/0,21=23,2.
Расчетные значения F-критериев больше критических значений (3,07; 2,49), что подтверждает существенное влияние на величину отходов толщины вырабатываемого стекла и режима отжига.
Приняв в качестве оценки дисперсии разброса отходов общий средний квадрат, равный 2,089 (%)2, можно определить возможное поле рассеивания отходов при надежности 99,73%, которое составит: 2(3√2,089)=8,67%.
Контрольные вопросы
1. Назначение дисперсионного анализа.
2. Основная идея однофакторного дисперсионного анализа. Формулирование нулевой гипотезы.
3. Оценка факторной суммы квадратов, обусловленной влиянием фактора А.
4. Оценка остаточной суммы квадратов, характеризующая рассеяние внутри группы.
5. Основная идея двухфакторного дисперсионного анализа.
6. Основное тождество дисперсионного анализа для случая двухфакторного анализа.
7. Проверка значимости расхождений, обнаруженных в средних по строкам и колонкам таблицы результатов наблюдений.
8. Оценка влияния факторов А и В на результативный признак.
Дата добавления: 2017-09-19; просмотров: 1213;
