Статистические оценки взаимосвязи двух временных рядов
Изучение причинно-следственных зависимостей переменных, представленных в виде временных рядов, является сложной задачей моделирования. Каждый уровень временного ряда, в общем случае, может описываться следующей моделью (1):
Yt = Ut + Vt + et , (8)
где Ut - трендовая компонента;
Vt – сезонная компонента;
et – случайная компонента.
t – уровни наблюдения, t=1, 2, 3,….
Наличие этих компонент может привести к серьезным проблемам при проведении корреляционно-регрессионного анализа данных временных рядов.
Поэтому на предварительном этапе анализа необходимо выявить структуру изучаемых временных рядов. Для этого необходимо построить совмещенные графики анализируемых рядов и провести визуальный анализ. И если в одном из временных рядов (результатная переменная) тенденция изменения может быть следствием того, что другая переменная (факторная) то же содержит такую же тенденцию или противоположную направленность, то это может быть причиной наличия коинтеграции временных рядов данных.
Под коинтеграцией понимается причинно следственная зависимость в уровнях двух или более временных рядов, которая выражается в совпадении или противоположной направленности их тенденций и случайной колеблемости.
Пример 2. Оценить тесноту связи временных рядов среднедушевого располагаемого дохода x(t) и среднедушевого расхода на конечное потребление y(t) в США в период с 1960 по 1991 годы. Исходные данные для расчетов даны в таблице 3 [3].
Таблица 3 - . Исходные данные для расчетов
| Годы, t | y(t) | x(t) | yр(t) | e(t) | Δe(t) | y*(t) | x*(t) |
| 6524,16 | 173,836 | ||||||
| 6632,98 | 107,023 | -66,813 | 1780,131 | 2003,008 | |||
| 6818,33 | 112,672 | 5,649 | 1940,03 | 2116,629 | |||
| 6942,82 | 146,182 | 33,51 | 1956,595 | 2102,789 | |||
| 7331,96 | 52,0365 | -94,1455 | 2134,596 | 2424,821 | |||
| 7671,31 | 31,6868 | -20,3497 | 2235,148 | 2480,33 | |||
| 7960,87 | 44,1329 | 12,4461 | 2300,929 | 2521,826 | |||
| 8230,13 | -67,1337 | -111,267 | 2235,298 | 2581,309 | |||
| 8492,95 | 13,0547 | 80,1884 | 2461,299 | 2650,083 | |||
| 8683,83 | 53,1705 | 40,1158 | 2438,307 | 2646,041 | |||
| 8931,89 | -89,8868 | -143,057 | 2372,252 | 2761,757 | |||
| 9149,51 | -127,513 | -37,6262 | 2474,499 | 2798,563 | |||
| 9428,92 | -3,9235 | 123,5895 | 2744,209 | 2926,805 | |||
| 9981,29 | -229,289 | -225,366 | 2772,788 | 3301,433 | |||
| 9814,38 | -212,381 | 16,908 | 2380,644 | 2676,874 | |||
| 9882,62 | -171,619 | 40,762 | 2600,719 | 2884,904 | |||
| 10146,4 | -25,3531 | 146,2659 | 2930,005 | 3116,107 | |||
| 10343,7 | 81,3077 | 106,6608 | 2930,4 | 3118,324 | |||
| -10,0473 | -91,355 | 3024,288 | 3404,857 | ||||
| 10927,4 | -60,4107 | -50,3634 | 2911,068 | 3263,335 | |||
| 10896,1 | -150,058 | -89,6473 | 2698,987 | 3090,121 | |||
| 11035,3 | -265,302 | -115,244 | 2812,587 | 3266,298 | |||
| 11026,1 | -244,08 | 21,222 | 2806,815 | 3144,482 | |||
| 11213,3 | -34,276 | 209,804 | 3194,929 | 3354,887 | |||
| 11840,3 | -223,335 | -189,059 | 3338,951 | 3884,566 | |||
| 12051,5 | -36,5067 | 186,8283 | 3412,612 | 3610,026 | |||
| 12322,6 | 13,3823 | 49,889 | 3438,893 | 3734,451 | |||
| 12316,2 | 251,837 | 238,4547 | 3433,192 | 3509,744 | |||
| 12634,3 | 268,697 | 16,86 | 3596,396 | 3859,928 | |||
| 12763,4 | 263,597 | -5,1 | 3472,329 | 3744,455 | |||
| 12877,7 | 173,25 | -90,347 | 3404,507 | 3764,785 | |||
| 12723,8 | 165,249 | -8,001 | 3224,735 | 3505,963 |
На рисунке 6 приведены графики изменения во времени среднедушевого располагаемого дохода x(t) и среднедушевого расхода на конечное потребление y(t) в США в период с 1960 по 1991 г.
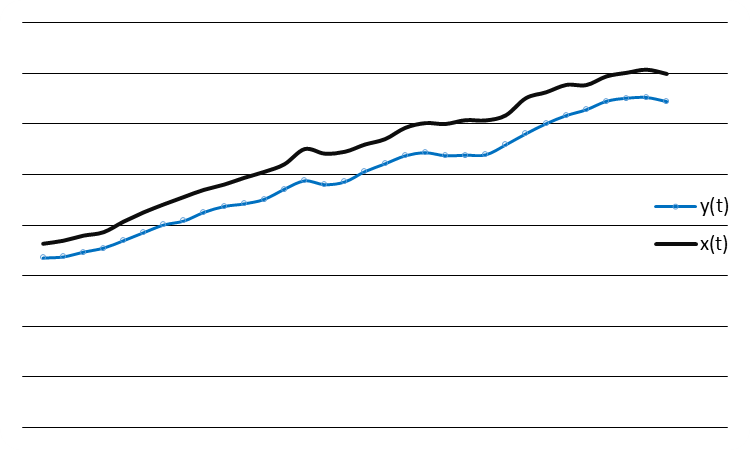
Рисунок 6 - Взаимосвязь временных рядов среднедушевого располагаемого дохода x(t) и среднедушевого расхода на конечное потребление y(t) (долл. США).
Визуальный анализ показывает, что тенденции изменения этих временных рядов совпадают. Для проверки гипотезы наличия коинтеграции между этими рядами построим регрессионную зависимость y=f(x) с помощью программы STATGRAPHICS Plus:
| Multiple Regression Analysis | ||||||
| ----------------------------------------------------------------------------- | ||||||
| Dependent variable: y(t) | ||||||
| ----------------------------------------------------------------------------- | ||||||
| Standard T | ||||||
| Parameter Estimate Error Statistic P-Value | ||||||
| ----------------------------------------------------------------------------- | ||||||
| CONSTANT -174,3 143,65 -1,21 0,23 | ||||||
| х(t) 0,92 0,0128 71,78 0,0000 | ||||||
| ----------------------------------------------------------------------------- | ||||||
| Analysis of Variance | ||||||
| ----------------------------------------------------------------------------- | ||||||
| Source Sum of Squares Df Mean Square F-Ratio P-Value | ||||||
| ----------------------------------------------------------------------------- | ||||||
| Model 1,23E8 1 1,23E8 5152,96 0,0000 | ||||||
| Residual 718861,0 30 23962,0 | ||||||
| ----------------------------------------------------------------------------- | ||||||
| Total (Corr.) 1,24E8 31 | ||||||
| R-squared = 99,42 percent | ||||||
| R-squared (adjusted for d.f.) = 99,40 percent | ||||||
| Standard Error of Est. = 154,8 | ||||||
| Mean absolute error = 121,945 | ||||||
| Durbin-Watson statistic = 0,519 |
Уравнение регрессии имеет вид:
yр(t) = -174,3 + 0,92x(t). (9)
Для проверки гипотезы отсутствия коинтеграции между рядами воспользуемся критерием Энгеля-Грангера [3]. Для этого рассчитаем уравнение регрессии вида:
Δe(t)=f(e(t-1)), (10)
где e(t-1), t=2, 3,..32 – остаток регрессионной модели (9);
Δe(t), t=2, 3,..32 – первые разности остатков.
Результаты расчета остатков приведены в таблице 3.Параметры уравнения регрессии (10), рассчитанные с помощью программы STATGRAPHICS Plus приведены ниже:
| Multiple Regression Analysis | |||||
| ----------------------------------------------------------------------------- | |||||
| Dependent variable: Δe(t) | |||||
| ----------------------------------------------------------------------------- | |||||
| Standard T | |||||
| Parameter Estimate Error Statistic P-Value | |||||
| ----------------------------------------------------------------------------- | |||||
| CONSTANT -1,73 18,94 -0,091 0,93 | |||||
| e (t-1) -0,27 0,127 -2,15 0,04 | |||||
| Analysis of Variance | |||||
| ----------------------------------------------------------------------------- | |||||
| Source Sum of Squares Df Mean Square F-Ratio P-Value | |||||
| ----------------------------------------------------------------------------- | |||||
| Model 51265,8 1 51265,8 4,62 0,04 | |||||
| Residual 322068,0 29 11105,8 | |||||
| ----------------------------------------------------------------------------- | |||||
| Total (Corr.) 373334,0 30 | |||||
| R-squared = 13,7 percent | |||||
| R-squared (adjusted for d.f.) = 10,75 percent | |||||
| Standard Error of Est. = 105,38 | |||||
| Mean absolute error = 82,83 | |||||
| Durbin-Watson statistic = 2,03 |
Уравнение регрессии имеет вид:
Δe(t)= -1,73 – 0,27e(t-1) (11)
Расчетное значение t-критерия значимости коэффициента регрессии при остатке e(t-1) по модулю равно 2,15, превышает критическое значение tкр=1,94. С вероятностью 95% можно отклонить нуль гипотезу и сделать вывод о коинтеграции анализируемых временных рядов.
Коэффициент детерминации уравнения регрессии (9) равен 99,42%, что говорит о тесной связи между расходами и среднедушевым доходом.
При расчете параметров уравнения регрессии (9) сталкиваемся с проблемой автокорреляции остатков модели. Наличие автокорреляции остатков проверяется по расчетной величине первого коэффициента автокорреляции r(1), который оказался больше критического значения, что свидетельствует о наличии положительной автокорреляции в остатках. Поэтому найденные оценки параметров уравнения регрессии (9) не являются эффективными ввиду нарушения предпосылок м.н.к.
Для получения новых оценок параметров уравнения регрессии воспользуемся обобщенным методом наименьших квадратов [3].
Найдем оценку коэффициента автокорреляции остатков первого порядка r(1):
r(1) = 0,74. (12)
Проведем пересчет исходных данных x и y в соответствии с формулами:
x* (t)= x(t) – r(1) x(t-1),
y* (t)= y(t) – r(1) y(t-1). (13)
Определим параметры уравнения регрессии y*=f(x*) обычным м.н.к.:
| Multiple Regression Analysis | ||||||
| ----------------------------------------------------------------------------- | ||||||
| Dependent variable: y* (t) | ||||||
| ----------------------------------------------------------------------------- | ||||||
| Standard T | ||||||
| Parameter Estimate Error Statistic P-Value | ||||||
| ----------------------------------------------------------------------------- | ||||||
| CONSTANT -83,94 110,25 -0,76 0,45 | ||||||
| x* (t) 0,93 0,035 26,2 0,0000 | ||||||
| Analysis of Variance | ||||||
| ----------------------------------------------------------------------------- | ||||||
| Source Sum of Squares Df Mean Square F-Ratio P-Value | ||||||
| ----------------------------------------------------------------------------- | ||||||
| Model 7,59E6 1 7,594E6 686,30 0,0000 | ||||||
| Residual 320894,0 29 11065,3 | ||||||
| ----------------------------------------------------------------------------- | ||||||
| Total (Corr.) 7,91E6 30 | ||||||
| R-squared = 95,94 percent | ||||||
| R-squared (adjusted for d.f.) = 95,8 percent | ||||||
| Standard Error of Est. = 105,19 | ||||||
| Mean absolute error = 82,0 | ||||||
| Durbin-Watson statistic = 2,11 |
Уравнение регрессии с пересчитанными данными имеет вид:
y* (t) = -83,94 + 0,93 x* (t). (14)
Свободный коэффициент исходного уравнения регрессии вычисляется по формуле:
a = a*/(1- r(1)) = -83,94/(1 – 0,74) = -322,85. (15)
Уравнение регрессии с уточненными коэффициентами принимает вид:
y(t) = -322,85 + 0,93 x(t). (16)
Полученные результаты являются статистически значимыми. Склонность к росту потребления в период с 1960 по 1991г. была равна 0,93. Это означает, что с увеличением среднедушевого дохода на 1 долл. среднедушевые расходы возрастают в среднем на 0,93 долл.
Если в результате проведенного анализа будет обнаружено отсутствие коинтеграции между рядами, либо на предварительном анализе совмещенных графиков в структуре изучаемых временных рядов обнаруживается тренда либо циклические колебания, то перед проведением дальнейших исследований взаимозависимости необходимо устранить тренд и циклическую компоненту из уровней каждого ряда. Наличие этих компонент может привести к завышению истинных показателей тесноты связи изучаемых временных рядов, если оба ряда будут содержать циклические колебания одинаковой периодичности, либо к занижению - в случае если только один из рядов будет содержать циклическую составляющую или периодичности колебаний циклических составляющих будут различными.
Методика исключения трендовой составляющей и циклической компоненты рассмотрена выше.
Дальнейший анализ взаимосвязи рядов проводят с использованием не исходных уровней, а центрированных рядов, получаемых путем вычитания из исходного ряда, составляющих тренда и циклической компоненты. Содержательная интерпретация параметров модели, рассчитанной по центрированным рядам, затруднительна. Ее можно использовать только для прогнозирования.
Пример 3. Расходы на конечное потребление и совокупный доход в течение 8-и лет, в условных единицах, приведены в таблице 4.
Таблица 4 - Расходы на конечное потребление и совокупный доход
| Год | Расходы на конечное потребление | Совокупный доход |
По табличным данным строим совмещенный график временных рядов (рис. 7).
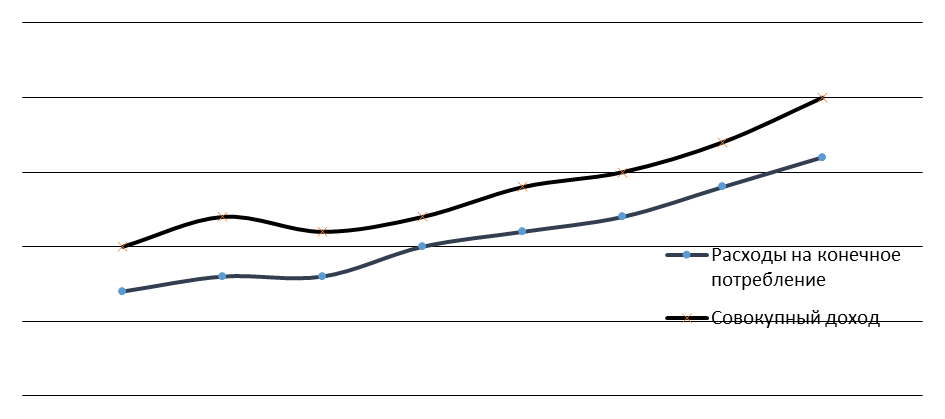
Рисунок 7- Взаимосвязь временных рядов расхода на конечное
потребление y(t) и совокупного дохода x(t)
На графике видно наличие тренда в анализируемых временных рядах. Корреляционно-регрессионный анализ, проведенный по исходным данным, дает следующие результаты:
y(t) = -2,047 + 0,922 x(t), R2 =95,5% , r = 0,98. (17)
Можно предположить, что полученные результаты (большое значение коэффициента парной корреляции r = 0,98) содержат ложную корреляцию, т.к. в каждом из рядов содержится трендовая компонента.
Выделим трендовые компоненты из исходных рядов. Как видно из графиков, тренд можно описать полиномом второго порядка.
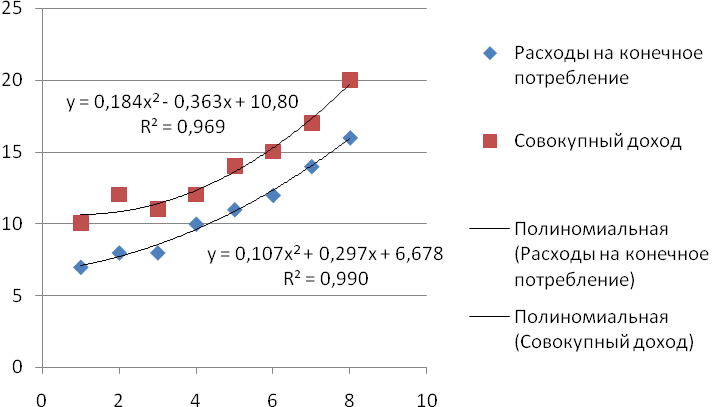
Рисунок 8 - Выделение тренда во временных рядах расхода
на конечное потребление и совокупного дохода.
Результаты построения модели регрессии по центрированным рядам y0 (t) и x0(t) приведены ниже:
y0(t)= 0,0026 + 0,269 x0(t). (18)
| Multiple Regression Analysis | ||||||
| ----------------------------------------------------------------------------- | ||||||
| Dependent variable: y0(t) | ||||||
| ----------------------------------------------------------------------------- | ||||||
| Standard T | ||||||
| Parameter Estimate Error Statistic P-Value | ||||||
| ----------------------------------------------------------------------------- | ||||||
| CONSTANT 0,0026 0,103 0,024 0,98 | ||||||
| x0 (t) 0,269 0,188 1,43 0,20 | ||||||
| ----------------------------------------------------------------------------- | ||||||
| Analysis of Variance | ||||||
| ----------------------------------------------------------------------------- | ||||||
| Source Sum of Squares Df Mean Square F-Ratio P-Value | ||||||
| ----------------------------------------------------------------------------- | ||||||
| Model 0,176 1 0,176 2,06 0,20 | ||||||
| Residual 0,514 6 0,0857 | ||||||
| ----------------------------------------------------------------------------- | ||||||
| Total (Corr.) 0,69 7 | ||||||
| R-squared = 25,52 percent | ||||||
| R-squared (adjusted for d.f.) = 13,10 percent | ||||||
| Standard Error of Est. = 0,29 | ||||||
| Mean absolute error = 0,1767 | ||||||
| Durbin-Watson statistic = 2,82 |
Регрессионная модель получилась не адекватной, т.к. расчетное значение критерия Фишера F=2,06 меньше табличного значения для уровня значимости 0,05, числа степеней свободы 1; 6 (F1; 6 = 5,99). Коэффициент корреляции между центрированными рядами незначимый, равен r = 0,5.
Связь между временными рядами на конечное потребление и совокупным доходом отсутствует. Уточненный анализ дал противоположные результаты по сравнению с тем, который мог получиться при не учете тренда в исходных временных рядах.
Контрольные вопросы
1. Модель аддитивного случайного процесса, интерпретация ее компонент.
2. Чем вызывается трендовая составляющая во временном ряду, ее аппроксимация?
3. Чем может вызываться периодическая составляющая во временном ряду, ее аппроксимация?
4. Как оценить случайную компоненту во временном ряду и чем она может вызываться?
5. Как оценивается точность разработанной модели временного ряда?
6. Для чего проверяют выполнение предпосылок м.н.к.?
7. Коинтеграции анализируемых временных рядов и чем она вызывается?
8. Обобщенный методом наименьших квадратов, в каких случаях он применяется?
9. Если обнаруживается тренд либо циклические колебания в исходных данных, то что необходимо выполнить перед дальнейшим анализом взаимосвязи рядов?
Дата добавления: 2017-09-19; просмотров: 1750;
