Оценка адекватности и точности трендовых моделей прогноза

Для анализа рядов динамики и их прогнозирования в простейшем случае можно использовать офисные информационные технологии, реализованные в электронной таблице EXCEL. В более сложных случаях используются модели на нечетких множествах, нейронных сетях и др.

Трендовая модель временного ряда считается адекватной, если она правильно отражает систематические компоненты временного ряда. Это эквивалентно требованию, чтобы остаточная компонента:

ξ_t = y_t - у_пр , t = 1, 2, ..,n

удовлетворяла свойствам случайной компоненты временного ряда: случайность колебаний, нормальность закона распределения, независимость уровней случайной компоненты.

Исследование остатков ξ_t полезно начинать с изучения их графика. 0н может показать наличие какой-то зависимости, не учтенной в модели. График остатков может показать необходимость перехода к нелинейной модели (квадратичной, полиномиальной, экспоненциальной) или включения в модель периодических компонент.

График остатков показывает и резко отклоня­ющиеся от модели наблюдения - выбросы. Подобным аномальным наблюдениям надо уделять особо пристальное внимание, так как их присутствие мо­жет грубо искажать значения оценок. Устранение эффектов вы­бросов может проводиться либо с помощью удаления этих точек из анализируемых данных, (эта процедура называется цензурированием),либо с помощью применения методов оценивания параметров, устойчи­вых к подобным грубым отклонениям.

Независимость остатков можно проверить расчетом первого коэффициента автокорреляции:

.

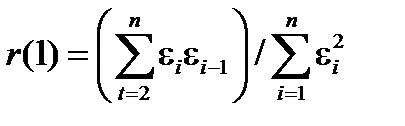Для принятия решения о наличии или отсутствии автокорреляции в исследуемом ряду фактическое значение коэффициента автокорреляции r(1) сопоставляется с табличным (критическим) значением для 5%-ного уровня значимости (вероятность допустить ошибку при принятии нулевой гипотезы о независимости уровней ряда). Если фактическое значение коэффициента автокорреляции меньше табличного, то гипотеза об отсутствии автокорреляции в ряду может быть принята, а если фактическое значение больше табличного – делают вывод о наличии автокорреляции в ряду динамики, т.е. зависимости остатков.

Для обнаружения гетероскедастич­ности обычно используют три теста, в которых делаются различные предположения о зависимости между дисперсией случайного члена и объясняющей переменной: тест ранговой корреляции Спирмена, тест Голдфельда-Квандта и тест Глейзера [Доугерти].

При малом объеме выборки для оценки гетероскедастичности может использоваться метод Голдфельда - Квандта. Данный тест используется для проверки такого типа гетероскедастичности, когда дисперсия остатков возрастает пропорционально квадрату фактора. При этом делается предположение, что, случайная составляющая ξ_t распределена нормально. Оценка нарушения гомоскедастичности по тесту Голдфельда-Квандта описывалась ранее в лекции 6.

Нормальность закона распределения остатков приближенно может быть оценена проверкой статистической значимости расчетных коэффициентов асимметрии А_с и эксцесса Э_с остатков, которые рассчитываются по формулам:

, ,

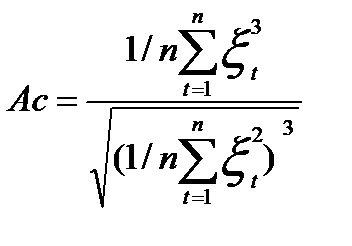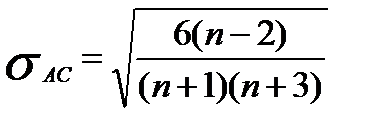где 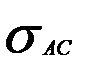- стандартная ошибка вычисления коэффициента асимметрии;

,

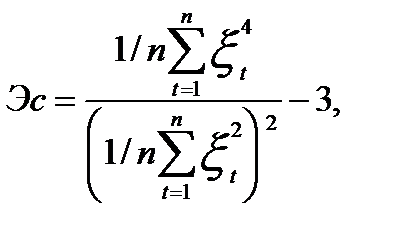
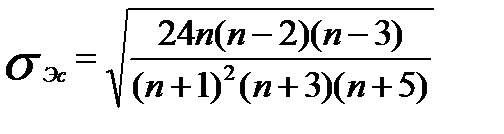где 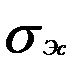- стандартная ошибка вычисления коэффициента эксцесса.

При одновременном выполнении неравенств:

| Ас| < 1,5 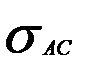, | Эс +6/(n+1)| < 1,5 ,

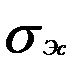гипотеза о нормальности закона распределения ξ_t принимается. При соотношении неравенств (>= 2σ) гипотеза нормальности распределения остатков отвергается.

Адекватность модели прогноза оценивается по значению коэффициента детерминации с использованием критерия Фишера. Рассчитывается значение коэффициента детерминации по формуле:

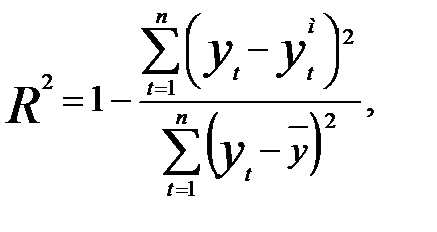
где 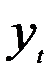- фактическое значение уровня временного ряда;

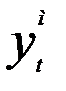- значение уровня временного ряда, рассчитанное по модели;

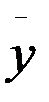- среднее арифметическое значение временного ряда.

Значимость коэффициента детерминации 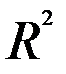проверяется сравнением расчетного значения критерия Фишера с критическим значением:

,

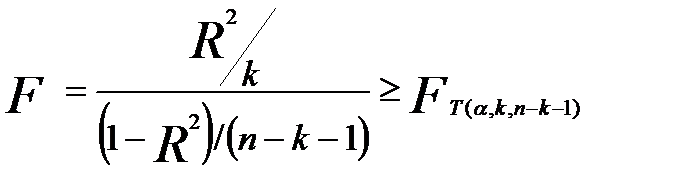где k – количество факторных переменных в функции тренда;

α – уровень значимости, принимается равным 0,05;

n – количество уровней в анализируемом временном ряду;

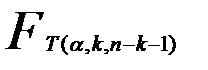- табличное значение критерия Фишера.

При выполнении неравенства F > F_T коэффициент детерминации принимается значимым, модель адекватно описывает анализируемый временной ряд.

Точность прогнозирования модели временного ряда оценивается с использованием ретроспективных данных, не использованных при построении модели временного ряда. Средняя квадратичная ошибка прогнозирования вычисляется по формуле:

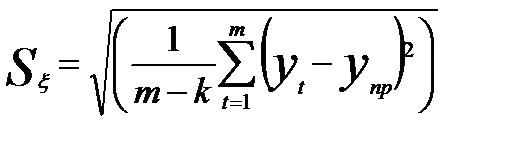
где 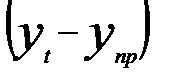- ошибка прогнозирования в точках t=1, 2, …, m;

k – число параметров в модели прогноза, при временном аргументе t значение k=1.

Контрольные вопросы

1) Для чего проводится анализ показателей работы объекта и их прогнозирование. Как используется эта информация в управлении?

2) Какая информационная технология и алгоритмы используются при прогнозировании?

3) Когда используется прогнозирование по среднему абсолютному изменению уровня ряда динамики?

4) Когда используется прогнозирование по среднему темпу роста уровня ряда динамики?

5) Когда используется прогнозирование по аналитическим временным функциям и корреляционным зависимостям?

6) Когда используется прогнозирование по среднему значению уровня ряда динамики?

7) Что понимается под точностью прогнозирования временного ряда?

8) На каких предпосылках основан прогноз рядов динамики?

9) Как зависит точность прогнозирования от интервала упреждения и почему?

Список используемой литературы

1. ГОСТ 24026-80. Исследовательские испытания. Планирование эксперимента. Термины и определения.

2. В.В. Налимов, Н.А. Чернова. Статистические методы планирования экстремальных экспериментов. М.: Наука, 1965. -340с.

3. Эконометрика: Учебник / Под ред. И.И. Елисеевой. - 2-е изд.; перераб. и доп. - М.: Финансы и статистика, 2005. - 576с.

4. Бородюк В.П., Лецкий Э.К. Статистическое описание промышленных объектов. М.: Энергия, 1971. -112 с.

5. Основы теории систем и системного анализа/ конспект лекций для специальности учет и аудит 95, Кривой Рог. Частное Учебное Заведение. –77с.

6 . Клячкин В.Н. Статистические методы в управлении качеством: компьютерные технологии: учеб. пособие / В.Н. Клячкин. – М.: Финансы и статистика, 2007. – 304 с.

7. Кремер Н.Ш. Теория вероятностей и математическая статистика. М.: ЮНИТИ-ДАНА, 2007. -573 с.

8. Яновский Л.П. Введение в эконометрику: учебное пособие / Л.П. Яновский, А.Г. Буховец; под. ред. Л.П. Яновского. -2 изд. доп.- М.: КОНКУРС, 2007.-256 с.

9. Макаров Р.И., Тарбеев В.В., Хорошева Е.Р. и др. Управление качеством листового стекла (флоат-способ): Учебное пособие. - М.: изд. Ассоциации строительных вузов, 2004. -152с.

10. http://life-prog.ru/

11. http://opds.sut.ru/

12. http://appmath.narod.ru/page11.html