Модели временных рядов
Модели, построенные по данным, характеризующим функционирование системы или процесс за ряд последовательных равноотстоящих моментов времени, называются моделями временных рядов, в дальнейшем-временными рядами. Простейшей является модель аддитивного случайного процесса, имеющая вид:
Yt = Ut + Vt + et , (1)
где Ut - трендовая компонента;
Vt – сезонная компонента;
et – случайная компонента.
t – уровни наблюдения, t=1, 2, 3,….
Для построения модели (1) необходимо получить оценки каждой компоненты. Для выделения составляющих компонент пользуются процедурами фильтрации, регрессионного и корреляционного анализов.
Относительно трендовой составляющей Ut предполагают, что она представляет некоторую гладкую функцию, описываемую полиномом небольшой степени. Для этого чаще всего используются следующие функции времени:
- линейная Ut = a+b t;
- парабола второго и, реже, более высокого порядков
Ut = a+b1 t +b2 t 2 +b3 t 3 +…+bn t n;
- экспонента Ut = e a+bt и др.
Параметры тренда определяются методом наименьших квадратов, в качестве независимой переменной выступает время t=1, 2, 3, .. , а в качестве зависимой переменной – уровни временного ряда Yt. Критерием отбора наилучшей формы тренда является значение коэффициента детерминации R2.
Пример 1.
Имеются данные о выработке продукции за 18 месяцев работы производственного участка (табл. 1)
Таблица 1- Данные о выработке продукции по месяцам
| Месяцы
|
|
|
|
|
|
|
| Выработка продукции
|
|
|
|
|
|
|
| Месяцы
|
|
|
|
|
|
|
| Выработка продукции
|
|
|
| ё
|
|
|
| Месяцы
|
|
|
|
|
|
|
| Выработка продукции
|
|
|
|
|
|
|
Требуется:
1) Построить график динамики выработки продукции.
2) Отобрать наилучшую форму тренда.
3) Выделить сезонную компоненту.
4) Построить аддитивную модель.
Решение.
Решение проводим с использованием ППП MS EXCEL. С использованием Мастера диаграмм строим график динамики выработки продукции (рис.1).
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEABgBrVsAA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbESPzYoCMRCE7wu+Q2jB25rRg8poFBEEV7w4+gDNpOcH k86QRGf27Y2wsMeiqr6iNrvBGvEiH1rHCmbTDARx6XTLtYL77fi9AhEiskbjmBT8UoDddvS1wVy7 nq/0KmItEoRDjgqaGLtcylA2ZDFMXUecvMp5izFJX0vtsU9wa+Q8yxbSYstpocGODg2Vj+JpFchb cexXhfGZO8+ri/k5XStySk3Gw34NItIQ/8N/7ZNWsFzC50v6AXL7BgAA//8DAFBLAQItABQABgAI AAAAIQDw94q7/QAAAOIBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsB Ai0AFAAGAAgAAAAhADHdX2HSAAAAjwEAAAsAAAAAAAAAAAAAAAAALgEAAF9yZWxzLy5yZWxzUEsB Ai0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABAAAAAAAAAAAAAAAAAAKQIAAGRycy9zaGFwZXhtbC54 bWxQSwECLQAUAAYACAAAACEABgBrVsAAAADbAAAADwAAAAAAAAAAAAAAAACYAgAAZHJzL2Rvd25y ZXYueG1sUEsFBgAAAAAEAAQA9QAAAIUDAAAAAA== " filled="f" stroked="f"> L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAd5//JL8A AADbAAAADwAAAGRycy9kb3ducmV2LnhtbERPS2rDMBDdF3IHMYXsarlepMGxEkohkIZu4uQAgzX+ EGlkJMV2bx8tCl0+3r86LNaIiXwYHCt4z3IQxI3TA3cKbtfj2xZEiMgajWNS8EsBDvvVS4WldjNf aKpjJ1IIhxIV9DGOpZSh6cliyNxInLjWeYsxQd9J7XFO4dbIIs830uLAqaHHkb56au71wyqQ1/o4 b2vjc3cu2h/zfbq05JRavy6fOxCRlvgv/nOftIKPNDZ9ST9A7p8AAAD//wMAUEsBAi0AFAAGAAgA AAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQSwEC LQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJlbHNQSwEC LQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBleG1sLnht bFBLAQItABQABgAIAAAAIQB3n/8kvwAAANsAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMvZG93bnJl di54bWxQSwUGAAAAAAQABAD1AAAAhAMAAAAA " filled="f" stroked="f"> L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAvDyDBb4A AADbAAAADwAAAGRycy9kb3ducmV2LnhtbERPy4rCMBTdC/5DuAPuNB0XUjpGGQYKHXFj9QMuze2D SW5KEm3n781CcHk47/1xtkY8yIfBsYLPTQaCuHF64E7B7VqucxAhIms0jknBPwU4HpaLPRbaTXyh Rx07kUI4FKigj3EspAxNTxbDxo3EiWudtxgT9J3UHqcUbo3cZtlOWhw4NfQ40k9PzV99twrktS6n vDY+c6dteza/1aUlp9TqY/7+AhFpjm/xy11pBXlan76kHyAPTwAAAP//AwBQSwECLQAUAAYACAAA ACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQIt ABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8ucmVsc1BLAQIt ABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hhcGV4bWwueG1s UEsBAi0AFAAGAAgAAAAhALw8gwW+AAAA2wAAAA8AAAAAAAAAAAAAAAAAmAIAAGRycy9kb3ducmV2 LnhtbFBLBQYAAAAABAAEAPUAAACDAwAAAAA= " filled="f" stroked="f"> L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEATO4dcsEA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbESP3YrCMBSE7xd8h3AE79ZUF5bSNYoIgi7eWPcBDs3p DyYnJYm2vr0RhL0cZuYbZrUZrRF38qFzrGAxz0AQV0533Cj4u+w/cxAhIms0jknBgwJs1pOPFRba DXymexkbkSAcClTQxtgXUoaqJYth7nri5NXOW4xJ+kZqj0OCWyOXWfYtLXacFlrsaddSdS1vVoG8 lPshL43P3O+yPpnj4VyTU2o2Hbc/ICKN8T/8bh+0gvwLXl/SD5DrJwAAAP//AwBQSwECLQAUAAYA CAAAACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBL AQItABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8ucmVsc1BL AQItABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hhcGV4bWwu eG1sUEsBAi0AFAAGAAgAAAAhAEzuHXLBAAAA2wAAAA8AAAAAAAAAAAAAAAAAmAIAAGRycy9kb3du cmV2LnhtbFBLBQYAAAAABAAEAPUAAACGAwAAAAA= " filled="f" stroked="f"> L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEArEsgncEA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbESP3YrCMBSE7xd8h3AE79ZUYZfSNYoIgi7eWPcBDs3p DyYnJYm2vr0RhL0cZuYbZrUZrRF38qFzrGAxz0AQV0533Cj4u+w/cxAhIms0jknBgwJs1pOPFRba DXymexkbkSAcClTQxtgXUoaqJYth7nri5NXOW4xJ+kZqj0OCWyOXWfYtLXacFlrsaddSdS1vVoG8 lPshL43P3O+yPpnj4VyTU2o2Hbc/ICKN8T/8bh+0gvwLXl/SD5DrJwAAAP//AwBQSwECLQAUAAYA CAAAACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBL AQItABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8ucmVsc1BL AQItABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hhcGV4bWwu eG1sUEsBAi0AFAAGAAgAAAAhAKxLIJ3BAAAA2wAAAA8AAAAAAAAAAAAAAAAAmAIAAGRycy9kb3du cmV2LnhtbFBLBQYAAAAABAAEAPUAAACGAwAAAAA= " filled="f" stroked="f"> L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAM9UbccEA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbESPzYoCMRCE7wu+Q2jB25rRw+4waxQRBF28OO4DNJOe H0w6QxKd8e2NIOyxqKqvqNVmtEbcyYfOsYLFPANBXDndcaPg77L/zEGEiKzROCYFDwqwWU8+Vlho N/CZ7mVsRIJwKFBBG2NfSBmqliyGueuJk1c7bzEm6RupPQ4Jbo1cZtmXtNhxWmixp11L1bW8WQXy Uu6HvDQ+c7/L+mSOh3NNTqnZdNz+gIg0xv/wu33QCvJveH1JP0CunwAAAP//AwBQSwECLQAUAAYA CAAAACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBL AQItABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8ucmVsc1BL AQItABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hhcGV4bWwu eG1sUEsBAi0AFAAGAAgAAAAhADPVG3HBAAAA2wAAAA8AAAAAAAAAAAAAAAAAmAIAAGRycy9kb3du cmV2LnhtbFBLBQYAAAAABAAEAPUAAACGAwAAAAA= " filled="f" stroked="f"> L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAlm2z6MIA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbESPzWoDMQyE74W8g1Ggt8ZODiVs44QQCKSll2z6AGKt /aG2vNhOdvv21aHQm8SMZj7tDnPw6kEpD5EtrFcGFHET3cCdha/b+WULKhdkhz4yWfihDIf94mmH lYsTX+lRl05JCOcKLfSljJXWuekpYF7FkVi0NqaARdbUaZdwkvDg9caYVx1wYGnocaRTT813fQ8W 9K0+T9vaJxM/Nu2nf79cW4rWPi/n4xuoQnP5N/9dX5zgG6GVZ2QCvf8FAAD//wMAUEsBAi0AFAAG AAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQ SwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJlbHNQ SwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBleG1s LnhtbFBLAQItABQABgAIAAAAIQCWbbPowgAAANwAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMvZG93 bnJldi54bWxQSwUGAAAAAAQABAD1AAAAhwMAAAAA " filled="f" stroked="f"> L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAkvkvML4A AADcAAAADwAAAGRycy9kb3ducmV2LnhtbERP24rCMBB9X/Afwgi+ramyLFKNIoKgiy9WP2BophdM JiWJtv69EYR9m8O5zmozWCMe5EPrWMFsmoEgLp1uuVZwvey/FyBCRNZoHJOCJwXYrEdfK8y16/lM jyLWIoVwyFFBE2OXSxnKhiyGqeuIE1c5bzEm6GupPfYp3Bo5z7JfabHl1NBgR7uGyltxtwrkpdj3 i8L4zP3Nq5M5Hs4VOaUm42G7BBFpiP/ij/ug0/zZD7yfSRfI9QsAAP//AwBQSwECLQAUAAYACAAA ACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQIt ABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8ucmVsc1BLAQIt ABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hhcGV4bWwueG1s UEsBAi0AFAAGAAgAAAAhAJL5LzC+AAAA3AAAAA8AAAAAAAAAAAAAAAAAmAIAAGRycy9kb3ducmV2 LnhtbFBLBQYAAAAABAAEAPUAAACDAwAAAAA= " filled="f" stroked="f"> L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEADWcU3L4A AADcAAAADwAAAGRycy9kb3ducmV2LnhtbERPy6rCMBDdC/5DGOHuNNWFSDWKCIJX7sbqBwzN9IHJ pCTR9v69EQR3czjP2ewGa8STfGgdK5jPMhDEpdMt1wpu1+N0BSJEZI3GMSn4pwC77Xi0wVy7ni/0 LGItUgiHHBU0MXa5lKFsyGKYuY44cZXzFmOCvpbaY5/CrZGLLFtKiy2nhgY7OjRU3ouHVSCvxbFf FcZn7ryo/szv6VKRU+pnMuzXICIN8Sv+uE86zZ8v4f1MukBuXwAAAP//AwBQSwECLQAUAAYACAAA ACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQIt ABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8ucmVsc1BLAQIt ABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hhcGV4bWwueG1s UEsBAi0AFAAGAAgAAAAhAA1nFNy+AAAA3AAAAA8AAAAAAAAAAAAAAAAAmAIAAGRycy9kb3ducmV2 LnhtbFBLBQYAAAAABAAEAPUAAACDAwAAAAA= " filled="f" stroked="f"> L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAE7QlNcIA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbESPT2sCMRDF74V+hzCF3mpWDyKrUaQgqHhx7QcYNrN/ MJksSequ3945FHqb4b157zeb3eSdelBMfWAD81kBirgOtufWwM/t8LUClTKyRReYDDwpwW77/rbB 0oaRr/SocqskhFOJBrqch1LrVHfkMc3CQCxaE6LHLGtstY04Srh3elEUS+2xZ2nocKDvjup79esN 6Ft1GFeVi0U4L5qLOx2vDQVjPj+m/RpUpin/m/+uj1bw50Irz8gEevsCAAD//wMAUEsBAi0AFAAG AAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQ SwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJlbHNQ SwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBleG1s LnhtbFBLAQItABQABgAIAAAAIQATtCU1wgAAANwAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMvZG93 bnJldi54bWxQSwUGAAAAAAQABAD1AAAAhwMAAAAA " filled="f" stroked="f"> L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEA03x9+b8A AADcAAAADwAAAGRycy9kb3ducmV2LnhtbERP24rCMBB9F/yHMMK+aWqFRbpGEUFQ2RfrfsDQTC+Y TEoSbf17s7Cwb3M419nsRmvEk3zoHCtYLjIQxJXTHTcKfm7H+RpEiMgajWNS8KIAu+10ssFCu4Gv 9CxjI1IIhwIVtDH2hZShasliWLieOHG18xZjgr6R2uOQwq2ReZZ9Sosdp4YWezq0VN3Lh1Ugb+Vx WJfGZ+6S19/mfLrW5JT6mI37LxCRxvgv/nOfdJqfr+D3mXSB3L4BAAD//wMAUEsBAi0AFAAGAAgA AAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQSwEC LQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJlbHNQSwEC LQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBleG1sLnht bFBLAQItABQABgAIAAAAIQDTfH35vwAAANwAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMvZG93bnJl di54bWxQSwUGAAAAAAQABAD1AAAAhAMAAAAA " filled="f" stroked="f"> L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAM9lAFr8A AADcAAAADwAAAGRycy9kb3ducmV2LnhtbERP24rCMBB9F/yHMMK+aWrBRbpGEUFQ2RfrfsDQTC+Y TEoSbf17s7Cwb3M419nsRmvEk3zoHCtYLjIQxJXTHTcKfm7H+RpEiMgajWNS8KIAu+10ssFCu4Gv 9CxjI1IIhwIVtDH2hZShasliWLieOHG18xZjgr6R2uOQwq2ReZZ9Sosdp4YWezq0VN3Lh1Ugb+Vx WJfGZ+6S19/mfLrW5JT6mI37LxCRxvgv/nOfdJqfr+D3mXSB3L4BAAD//wMAUEsBAi0AFAAGAAgA AAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQSwEC LQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJlbHNQSwEC LQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBleG1sLnht bFBLAQItABQABgAIAAAAIQAz2UAWvwAAANwAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMvZG93bnJl di54bWxQSwUGAAAAAAQABAD1AAAAhAMAAAAA " filled="f" stroked="f"> L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEArEd7+r8A AADcAAAADwAAAGRycy9kb3ducmV2LnhtbERPzYrCMBC+C75DGGFvmtqDK12jiCCo7MW6DzA00x9M JiWJtr69WVjY23x8v7PZjdaIJ/nQOVawXGQgiCunO24U/NyO8zWIEJE1Gsek4EUBdtvpZIOFdgNf 6VnGRqQQDgUqaGPsCylD1ZLFsHA9ceJq5y3GBH0jtcchhVsj8yxbSYsdp4YWezq0VN3Lh1Ugb+Vx WJfGZ+6S19/mfLrW5JT6mI37LxCRxvgv/nOfdJqff8LvM+kCuX0DAAD//wMAUEsBAi0AFAAGAAgA AAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQSwEC LQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJlbHNQSwEC LQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBleG1sLnht bFBLAQItABQABgAIAAAAIQCsR3v6vwAAANwAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMvZG93bnJl di54bWxQSwUGAAAAAAQABAD1AAAAhAMAAAAA " filled="f" stroked="f">
Рисунок 1- График выработки продукции по месяцам
График (рис.1) характеризует убывающую тенденцию выработки продукции с периодическими колебаниями. Проведем подбор тренда путем наложения линий тренда. Одновременно установим режим отображения уравнения регрессии, описывающего тренд и коэффициента детерминации. В таблице 2 приведены характеристики подбираемых линий тренда.
Таблица 2 - Подбор линий тренда м.н.к.
| Вид тренда
| Коэффициент детерминации
| Уравнение тренда
|
| Линейный
| 61%
| Ut = 665390 -12707 t
|
| Парабола
| 61,5%
| Ut = -50,31t 2 – 11751 t + 662203
|
| Экспонента
| 62,4%
| Ut = 672830e - 0,0235 t
|
Все три вида тренда адекватно описывают характер изменения выработки продукции во времени. Коэффициенты детерминации статистически значимы при уровне значимости 0,05, расчетные значения критерия Фишера превышают табличные данные. Для математического описания тренда выбираем более простое линейное уравнение.
Для выделения сезонной компоненты совместно со случайной составляющей (Vt +et), из исходного ряда Yt вычитаем трендовую компоненту Ut. При этом получаем центрированный временной ряд:
(Vt +et) = Yt - Ut (2)
График центрированного временного ряда отображен на рис.2.
Рисунок 2 - График компонент (Vt +et) в динамическом ряду выработки
продукции
Для определения периода циклической компоненты Vt вычисляем автокорреляционную функцию центрированного временного ряда (рис.3). На графике просматривается периодическая составляющая с периодом
(13-1)=12 месяцев и временным сдвигом (12-3)=9 месяцев. Амплитуда гармоники может быть приближенно оценена с помощью дисперсию центрированного временного ряда. Из условия аддитивности модели вытекает баланс дисперсий центрированного ряда:
S2 (Vt +et) = S2 (Vt) + S2(et) , (3)
где S2 (Vt +et) – оценка дисперсии центрированного временного ряда;
S2(Vt) - оценка дисперсии сезонной (гармонической) компоненты, равная квадрату амплитуды гармоники;
S2(et) – оценка дисперсии случайной компоненты.
Рисунок 3 - Автокорреляционная функция центрированного временного ряда
Если пренебречь дисперсией случайной компоненты, то за амплитуду гармонической составляющей можно принять (оценка сверху) стандартное отклонение центрированного ряда. В рассматриваемом примере это будет:
AVt = S(Vt) = 53660.
Амплитуда гармоники может быть уточнена по критерию минимума случайной компоненты временного ряда. На графике (рис.4) приведены совмещенные компоненты (Vt+et) и гармоническая компонента Vt с уточненной амплитудой, равной 50000:
Vt = 50000Sin((2π/12)t + 2π(2,85/4)). (4)
Для выделения случайной компоненты et из центрированного временного ряда (Vt+et) вычитаем гармоническую компоненту Vt .
Рисунок 4- График центрированного ряда (Vt +et) с наложением гармонической компоненты Vt = 50000Sin((2π/12)t + 2π(2,85/4))
График случайной компоненты приведен на рис. 5.
Рисунок 5- График случайной компоненты временного ряда выработки
продукции
Случайная компонента et имеет следующие параметры:
- среднее значение равно -226,3 (шт/месяц), что статистически незначимо при уровне значимости 0,05;
- оценка дисперсии равна 13,7 1 (шт/месяц)2.
После подстановки в исходное уравнение (1) всех компонент, временной ряд выработки продукции, уровни которых представлены в табл.1, описывается следующей аддитивной моделью:
Yt = -12707t + 665390 + 50000Sin((2π/12)t + 2π(2,85/4)) + et . (5)
Адекватность модели (5) оцениваем по результатам анализа случайной компоненты et. Проверяем выполнение предпосылок м.н.к.
- Случайность остатков модели определяем по числу точек перегиба:
p = 11 > pк =9, (6)
где pк = [2(n-2)/3-2√(16n-29)/90].
- Для определения независимости значений уровней случайной компоненты можно воспользоваться первым коэффициентом автокорреляции:
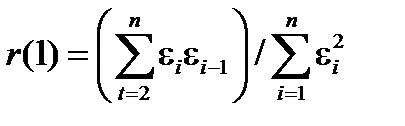 . (7)
. (7)
Для принятия решения о наличии или отсутствии автокорреляции в исследуемом ряду фактическое значение коэффициента автокорреляции r(1) сопоставляется с табличным (критическим) значением для 5%-го уровня значимости (вероятность допустить ошибку при принятии нулевой гипотезы о независимости уровней ряда). Если фактическое значение коэффициента автокорреляции меньше табличного, то гипотеза об отсутствии автокорреляции в ряду принимается. Если фактическое значение больше табличного – делают вывод о наличии автокорреляции в ряду динамики.
Для обнаружения гетероскедастичности обычно используют три теста, в которых делаются различные предположения о зависимости между дисперсией случайного члена и объясняющей переменной: тест ранговой корреляции Спирмена, тест Голдфельда-Квандта и тест Глейзера [Доугерти].
При малом объеме выборки для оценки гетероскедастичности может использоваться тест Голдфельда - Квандта.
Данный тест используется для проверки такого типа гетероскедастичности, когда дисперсия остатков возрастает пропорционально квадрату фактора. При этом делается предположение, что, случайная составляющая et распределена нормально. Алгоритм применения теста Голдфельда – Квандта для оценки гетероскедастичности описан в лекции 2 на стр.16-17 данного пособия.
В рассматриваемом примере все предпосылки м.н.к. выполняются, что подтверждает адекватность разработанной модели (5).
Оценим точность разработанной модели. Для этого вычисляем среднюю абсолютную и среднюю относительную ошибку. Расчеты показали следующие результаты:
- средняя абсолютная ошибка разработанной модели равна 25877,8 шт./месяц;
- средняя относительная ошибка равна 4,7%.
Приведем интерпретацию результатов исследований с учетом особенностей анализируемого производственного процесса. В рассматриваемом временном интервале работа участка характеризуется нестабильностью. Среднее абсолютное уменьшение выработки изделий в течение месяца составляет:
∆yср = 12707 шт.
Темп уменьшения выработки изделий в последнем месяце 2007г. составил величину (12707/449371)100%=2,83%.
Сезонная компонента Vt отражает увеличение выработки изделий в зимние месяцы года (декабрь-январь) и уменьшение в летние месяцы (июнь-июль) на величину, примерно равную, 50000 шт./месяц. Одной из причин может быть колебания спроса.
Дата добавления: 2017-09-19; просмотров: 833;
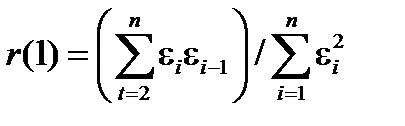 . (7)
. (7)