Статистика Дарбина-Уотсона.
Статистическая значимость коэффициентов регрессии и близкое к единице значение коэффициента детерминации R2 не гарантируют высокое качество уравнения регрессии. Для иллюстрации этого факта весьма нагляден пример, в котором анализируется зависимость реального объема потребления CONS (млрд. $, в ценах 1982 года) от численности населения POP (млн. чел.) в США в 1931—1990 годах. Корреляционное поле статистических данных изображено на рис1.
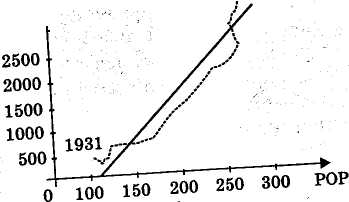
Рис.1. Корреляционное поле статистических данных
Линейное уравнение регрессии, построенное по МНК по реальным статистическим данным, имеет вид: СONS =-1817,3 + 16,7РОР. Стандартные ошибки коэффициентов Sb0= 84,7, Sb1=0,46. Следовательно, их t-статистики tb0=-21,4 , tb1=36,8. Эти значения существенно превышают 3, что свидетельствует о статистической значимости коэффициентов. Коэффициент детерминации R2 = 0,96 (т.е. уравнение «объясняет» 96% дисперсии объема потребления). Однако по расположению точек на корреляционном поле видно, что зависимость между POP и CONS не является линейной, а будет скорее экспоненциальной. Для качественного прогноза уровня потребления линейная функция, безусловно, не может быть использована. Таким образом, при весьма хороших значениях t-статистик и F-статистики предложенное уравнение регрессии не может быть признано удовлетворительным (отметим, что R =0,96, скорее всего, в силу того, что и CONS и POP имели временной тренд). Можно ли определить причину этого?
Нетрудно заметить, что в данном случае не выполняются необходимые предпосылки МНК об отклонениях ei точек наблюдений от линии регрессии. Эти отклонения явно не обладают постоянной дисперсией и не являются взаимно независимыми. Нарушение необходимых предпосылок делает неточными полученные оценки коэффициентов регрессии, увеличивая их стандартные ошибки, и обычно свидетельствует о неверной спецификации самого уравнения.
Поэтому следующим этапом проверки качества уравнения регрессии является проверка выполнимости предпосылок МНК.
Оценивая линейное уравнение регрессии, мы предполагаем, что реальная взаимосвязь переменных линейна, а отклонения от регрессионной прямой являются случайными, независимыми друг от друга величинами с нулевым математическим ожиданием и постоянной дисперсией. Если эти предположения не выполняются, то оценки коэффициентов регрессии не обладают свойствами несмещенности, эффективности и состоятельности, и анализ их значимости будет неточным.
Причинами, по которым отклонения не обладают перечисленными выше свойствами, могут быть либо нелинейный характер зависимости между рассматриваемыми переменными, либо наличие не учтенного в уравнении существенного фактора. Действительно, при нелинейной зависимости между переменными отклонения от прямой регрессии не случайно распределены вокруг нее, а обладают определенными закономерностями, которые зачастую выражаются в существенном преобладании числа пар соседних отклонений ei-1 и ei с совпадающими знаками над числом пар с противоположными знаками.
При статистическом анализе уравнения регрессии на начальном этапе часто проверяют выполнимость одной предпосылки, а именно: условия статистической независимости отклонений между собой. Поскольку значения ei теоретического уравнения регрессии Y=β0+β1x+e остаются неизвестными ввиду неопределенности истинных значений коэффициентов регрессии, то проверяется статистическая независимость их оценок - отклонений ei, i=1,2,...,n. При этом обычно проверяется их некоррелированность, являющаяся необходимым, но недостаточным условием независимости. Причем проверяется некоррелированность не любых, а только соседних величин ei. Соседними обычно считаются соседние во времени (при рассмотрении временных рядов) или по возрастанию объясняющей переменной X (в случае перекрестной выборки) значения еi
Для этих величин несложно рассчитать коэффициент корреляции, называемый в этом случае коэффициентом автокорреляции первого порядка: При этом учитывается, что M(ei) = 0, i=1,2,...,n.
На практике для анализа коррелированности отклонений вместо коэффициента корреляции используют тесно с ним связанную статистику Дарбина— Уотсона DW, рассчитываемую по формуле:
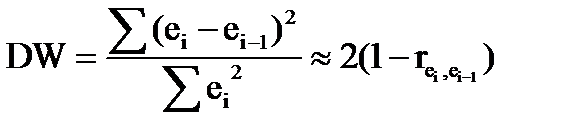
Если ei = еi-1, то rei.e-1=1 и DW = 0. Если еi=-еi-1; , то rei.e-1=-1 и DW = 4. Во всех других случаях 0 < DW < 4 .
К этому же результату можно подойти с другой стороны. Если каждое следующее отклонение ei приблизительно равно предыдущему, ei-1, то каждое слагаемое (e1-ei-1) в числителе дроби близко к нулю. Тогда, очевидно, числитель дроби будет существенно меньше знаменателя и, следовательно, статистика DW окажется близкой к нулю.
Например, для зависимости CONS и POP (рис. 1) DW = 0,045, что очень близко к нулю и подтверждает наличие положительной автокорреляции остатков первого порядка (линейной зависимости между остатками).
В другом крайнем случае, когда точки наблюдений поочередно отклоняются в разные стороны от линии регрессии, случай отрицательной автокорреляции остатков первого порядка. При случайном поведении отклонений можно предположить, что в одной половине случаев знаки последовательных отклонений совпадают, а в другой — противоположны. Так как абсолютная величина отклонений в среднем предполагается одинаковой, то можно считать, что в половине случаев ei = еi-1, а в другой еi=-еi-1. Тогда DW =2
Таким образом, необходимым условием независимости случайных отклонений является близость к двойке значения статистики Дарбина—Уотсона. Это означает, что построенная линейная регрессия, вероятно, отражает реальную зависимость.
Возникает вопрос, какие значения DW можно считать статистически близкими к двум?
Для ответа на этот вопрос разработаны специальные таблицы критических точек статистики Дарбина—Уотсона, позволяющие при данном числе наблюдений n, количестве объясняющих переменных m и заданном уровне значимости α определять границы приемлемости (критические точки) наблюдаемой статистики DW. Для заданных α,n,m в таблице указываются два числа: dl— нижняя граница и du — верхняя граница. Для проверки гипотезы об отсутствии автокорреляции остатков используется числовой отрезок, изображенный на рис. 2.
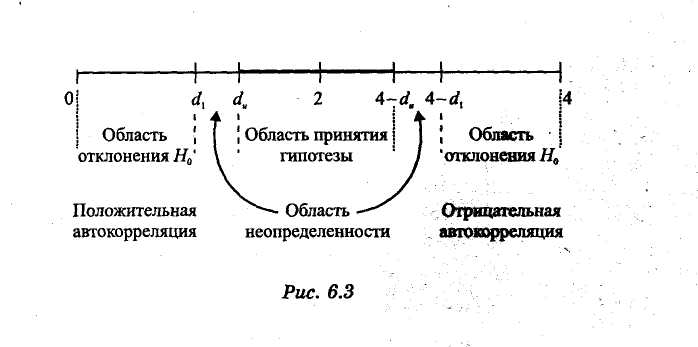
Рис.2. Числовой отрезок.
Выводы осуществляются по следующей схеме.
- Если DW<dl, то это свидетельствует о положительной автокорреляции остатков.
- Если DW>4-dl, то это свидетельствует об отрицательной автокорреляции остатков.
- При du<DW< 4-du гипотеза об отсутствии автокорреляции остатков принимается.
- Если dl<DW<du, или 4-du<DW<4-dl , то гипотеза об отсутствии автокорреляции не может быть ни принята, ни отклонена.
Не обращаясь к таблице критических точек Дарбина—Уотсона, можно пользоваться «грубым» правилом и считать, что автокорреляция остатков отсутствует, если 1,5<DW<2,5. Для более надежного вывода целесообразно обращаться к табличным значениям.
При наличии автокорреляции остатков полученное уравнение регрессии обычно считается неудовлетворительным.
Пример. Анализируется объем S сбережений домохозяйства за 10 лет. Предполагается, что его размер St в текущем году t зависит от величины yt-\ располагаемого дохода Y в предыдущем году и от величины Zt реальной процентной ставки Z в рассматриваемом году. Статистические данные представлены в таблице:
| Год | |||||||||||
| Y, тыс. у.е. | |||||||||||
| Z, % | |||||||||||
| S, тыс. у.е. |
Необходимо:
а) по МНК оценить коэффициенты линейной регрессии S =β0+β1Y+β2Z;
б) оценить статистическую значимость найденных эмпирических коэффициентов регрессии b0, b1, b2;
в) построить 95% -е доверительные интервалы для найденных коэффициентов;
г) вычислить коэффициент детерминации R2 и оценить его статистическую значимость при α = 0,05;
д) определить, какой процент разброса зависимой переменной объясняется данной регрессией (значимость R2 по Фишеру);
е) вычислить статистику DW Дарбина—У отсона и оценить наличие автокорреляции;
ж) сделать выводы по качеству построенной модели;
з) спрогнозировать средний объем сбережений в 1991 году, если предполагаемый доход составит 270 тыс. у.е., а процентная ставка будет равна 5,5.
Расчет коэффициентов проводится по формулам: b0= 5,9619423; b1= 0,126189; b2= 3,24841/
Найденное уравнение позволяет рассчитать модельные значения sj зависимой переменной S и вычислить отклонения ei реальных значений от модельных:
| Год | S | S* | ei | ei2 | ei-ei-1 | (ei-ei-1)2 |
| 22,48852 | -2,48852 | 6,19273 | - | -. | ||
| 23,73041 | 1,269594 | 1,61187 | 3,75811 | 14,12339 | ||
| 31,00991 | -1,00991 | 1,01992 | -2,27950 | 5,19612 | ||
| 28,69796 | 1,30204 | 1,69523 | 2,31194 | 5,34507 | ||
| 33,49369 | 1,50631 | 2,26896 | 0,20427 | 0,04173 | ||
| 37,04753 | 0,95247 | 0,90719 | -0,55384 | 0,30674 | ||
| 39,53131 | 0,46869 | 0,21967 | -0,48378 | 0,23404 | ||
| 38,46125 | -0,46125 | 0,21275 | -0,92994 | 0,86479 | ||
| 45,74076 | -1,74076 | 3,03024 | -1,27951 | 1,63714 | ||
| 51,77838 | -1,77838 | 3,16263 | -0,03762 | 0,00141 | ||
| 53,02027 | 1,97973 | 3,91933 | 3,78811 | 14,12332 | ||
| Сумма | ≈0 | 24,24058 | - | 41,87375 | ||
| Среднее | 36,81818 | 36,81818 | - | - | - | - |
Проанализируем статистическую значимость коэффициентов регрессии, предварительно рассчитав их стандартные ошибки. Стандартная ошибка регрессии S=1,7407. Следовательно, дисперсии и стандартные ошибки коэффициентов равны:
Sb0= 1,8929; Sb1= 0,0212; Sb2= 1,0146.
Рассчитаем соответствующие t-статистики: tb0= 1,565; tb1= 5,858; tb2= 3,503.
На первый взгляд (используя «грубое» правило), только статистическая значимость свободного члена вызывает сомнения. Два других коэффициента имеют t-статистики, превышающие тройку, что является признаком их высокой статистической значимости. Однако убедимся в таком выводе на основе более детального анализа.
Для использования таблиц критических точек необходимо выбрать требуемый уровень значимости. Обычно это прерогатива исследователя.
Вопросы для повторения
1. Какая существует связь между линейным коэффициентом корреляции и коэффициентом регрессии?
2. Каким образом оценить точность полученной модели регрессии?
3. Какими критериями пользуются при оценке качества построенной регрессионной модели?
4. Как строятся доверительные интервалы для регрессионной модели?
5. Может ли регрессия нелинейная по параметрам быть приведена к линейному виду?
6. Как осуществляется прогноз показателей по регрессионной модели?
Резюме по теме
Самым распространенным методом оценки параметров уравнения множественной линейной регрессии является метод наименьших квадратов (МНК).
Эмпирические коэффициенты множественной линейной регрессии определяются по формуле В = (ХТ X)-1XTY.
Для построения интервальной оценки коэффициента βj - строится t-статистика
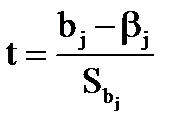
имеющая распределение Стьюдента с числом степеней свободы ν= n-m-1.
Статистическая значимость коэффициентов регрессии и близкое к единице значение коэффициента детерминации R2 не гарантируют высокое качество уравнения регрессии.
Дата добавления: 2017-09-19; просмотров: 426;
