Инструмент анализа данных - Описательная статистика
Чем больше характеристик распределения случайной величины известно, тем точнее мы можем судить об описываемых ею процессах. Инструмент Описательная статистика автоматически вычисляет наиболее широко используемые в практическом анализе характеристики распределений. При этом значения могут быть определены сразу для нескольких исследуемых переменных.
Определим параметры описательной статистики для переменных V,Q,P,NCF,NPV. Для этого необходимо выполнить следующие шаги.
1. Выбрать в главном меню тему Сервис, пункт Анализ данных. Результатом выполнения этих действий будет появление диалогового окна Анализ данных, содержащего список инструментов анализа.
2.Выбрать из списка Инструменты анализа пункт Описательная статистика. Результатом будет появление окна диалога инструмента Описательная статистика (Рисунок 15.)
3. Заполнить поля диалогового окна.
Рисунок 15. Заполнение полей диалогового окна Описательная статистика.
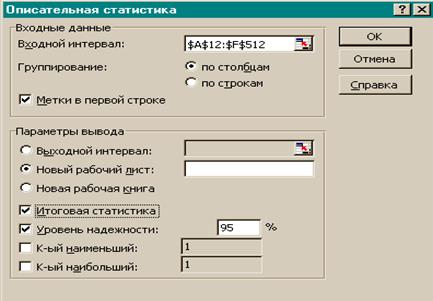
Таблица 22. Описательная статистика для исследуемых переменных
| Переменные расходы (V) | Количество (Q) | Цена (P) | Поступления (NCF) | ЧСС (NPV) | |
| Среднее | 29,94367 | 211,633 | 48,66328 | 1487,224 | 3637,75 |
| Стандартная ошибка | 0,160212 | 2,46609 | 0,246654 | 25,86201 | 98,03735 |
| Медиана | 30,15143 | 214,8309 | 48,98313 | 1478,252 | 3603,739 |
| Мода | 26,03967 | 151,54 | 42,65288 | 867,0263 | 1286,712 |
| Стандартное отклонение | 3,582452 | 55,14345 | 5,515357 | 578,292 | 2192,182 |
| Дисперсия выборки | 12,83396 | 3040,8 | 30,41916 | 334421,7 | |
| Эксцесс | 0,209999 | 0,209999 | 0,209999 | 0,59754 | 0,59754 |
| Асимметричность | -0,03985 | -0,03985 | -0,03985 | 0,450358 | 0,450358 |
| Интервал | 22,834 | 351,4759 | 35,15404 | 3791,825 | |
| Минимум | 19,29853 | 47,77592 | 32,27457 | 107,9769 | -1590,68 |
| Максимум | 42,13253 | 399,2518 | 67,42861 | 3899,802 | 12783,32 |
| Сумма | 14971,84 | 105816,5 | 24331,64 | 743612,1 | |
| Счет | |||||
| Наибольший(1) | 42,13253 | 399,2518 | 67,42861 | 3899,802 | 12783,32 |
| Наименьший(1) | 19,29853 | 47,77592 | 32,27457 | 107,9769 | -1590,68 |
| Уровень надежности(95,0%) | 0,314773 | 4,845193 | 0,484608 | 50,81178 | 192,6166 |
Результатом выполнения указанных действий будет формирование отдельного листа, содержащего вычисленные характеристики описательной статистики для исследуемых переменных. (Таблица 22. Описательная статистика для исследуемых переменных)
Многие из приведенных в данной таблице характеристик нам уже хорошо знакомы, а их значения уже определены с помощью соответствующих функций на листе Результаты анализа. Поэтому рассмотрим лишь те из них, которые не упоминались ранее.
Вторая строка таблицы содержит значения стандартных ошибок e для средних величин распределений. Другими словами, среднее, или ожидаемое, значение случайной величины М(Е) определено с погрешностью 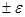 .
.
Медиана –это значение случайной величины, которое делит площадь, ограниченную кривой распределения, пополам (т.е. середина численного ряда или интервала). Как и математическое ожидание, медиана является одной из характеристик центра распределения случайной величины. В симметричных распределениях значение медианы должно быть равным или достаточно близким к математическому ожиданию.
Мода– наиболее вероятное значение случайной величины (наиболее часто встречающееся значение в интервале данных). Для симметричных распределений мода равна математическому ожиданию. Иногда мода может отсутствовать.
Эксцесс характеризует остроконечность (положительное значение) или пологость (отрицательное значение) распределения по сравнению с нормальной кривой. Теоретически эксцесс нормального распределения должен быть равен 0. Однако на практике для генеральных совокупностей больших объемов его малыми значениями можно пренебречь.
Асимметричность(коэффициент асимметрии или скоса –s) характеризует смещение распределения относительно математического ожидания. При положительном значении коэффициента распределение скошено вправо, т.е. его более длинная часть лежит правее центра (математического ожидания), и наоборот. Для нормального распределения коэффициент асимметрии равен 0. На практике его малыми значениями можно пренебречь. Оставшиеся показатели описательной статистики менее интересны.
Величина Интервал определяется как разность между максимальным и минимальным значениями случайной величины.
Параметры Счет и Сумма представляют собой число значений в заданном интервале и их сумму соответственно.
Последняя характеристика Уровень надежностипоказывает величину доверительного интервала для математического ожидания согласно заданному уровню надежности или доверия. По умолчанию уровень надежности принят равным 95%.
Можно указать другой уровень надежности путем ввода соответствующего значения в поле Уровень надежности диалогового окна Описательная статистика.Следует отметить, что чем выше принятый уровень надежности, тем больше величина доверительного интервала для среднего.
Рассчитать доверительный интервал для среднего значения можно также с помощью специальной статистической функции ДОВЕРИТ().
Дополнение Анализ данныхсодержит целый ряд других полезных инструментов, позволяющих быстро и эффективно осуществить требуемый вид обработки данных.
Имитационное моделирование позволяет учесть максимально возможное число факторов внешней среды для поддержки принятия управленческих решений и является наиболее мощным средством анализа инвестиционных рисков. Необходимость его применения в отечественной финансовой практике обусловлена особенностями российского рынка, характеризующегося субъективизмом, зависимостью от внеэкономических факторов и высокой степенью неопределенности.
Результаты имитации могут быть дополнены вероятностным и статистическим анализом и в целом обеспечивают менеджера наиболее полной информацией о степени влияния ключевых факторов на ожидаемые результаты и возможных сценариях развития событий.
К недостаткам рассмотренного подхода следует отнести:
· Трудность понимания и восприятия менеджерами имитационных моделей, учитывающих большое число внешних и внутренних факторов, вследствие их математической сложности и объемности;
· При разработке реальных моделей может возникнуть необходимость привлечения специалистов или научных консультантов со стороны;
· Относительную неточность полученных результатов по сравнению с другими методами численного анализа и др.
Несмотря на отмеченные недостатки, в настоящее время имитационное моделирование является основой для создания новых перспективных технологий управления и принятия решений в сфере бизнеса, а развитие вычислительной техники и программного обеспечения делает этот метод все более доступным для широкого круга специалистов-практиков.
Дата добавления: 2019-04-03; просмотров: 1503;
