Статистический анализ результатов имитации

В анализе стохастических процессов важное значение имеют статистические взаимосвязи между случайными величинами. В качестве количественных характеристик подобных взаимосвязей в статистике используют два показателя ковариацию и корреляцию.

Ковариациявыражает степень статистической зависимости между двумя множествами данных и определяется из соотношения:

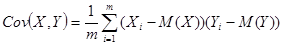
где X,Y –множество значений случайных величин размерности m ; М(Х) – математическое ожидание случайной величины Х; М(Y) – математическое ожидание случайной величины Y .

Как следует из этой формулы, положительная ковариация наблюдается в том случае, когда большим значениям случайной величины Х соответствуют большие значения случайной величины Y, т.е. между ними существует тесная прямая взаимосвязь. Отрицательная ковариация будет иметь место при соответствии малым значениям случайной величины Х больших значений случайной величины Y. При слабо выраженной зависимости значение показателя ковариации близко к 0.

Ковариация зависит от единиц измерения исследуемых величин, что ограничивает ее применение на практике. Более удобным для использования в анализе является производный от нее показатель – коэффициент корреляции R , вычисляемый по формуле:

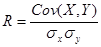
Коэффициент корреляции обладает теми же свойствами, что и ковариация, однако является безразмерной величиной и принимает значения от –1 (характеризует линейную обратную взаимосвязь) до +1 (характеризует линейную прямую взаимосвязь). Для независимых случайных величин значение коэффициента корреляции близко к 0.

Определение количественных характеристик для оценки тесноты взаимосвязи между случайными величинами в MS Excel может быть осуществлено двумя способами:

· С помощью статистических функций КОВАР() и КОРРЕЛ();

· С помощью специальных инструментов статистического анализа.

Если число исследуемых переменных больше двух, более удобным является использование инструмента анализа.