Имитационная модель опроса прохожих
Предположим, опрашивают прохожих на улице города. Требуется оценить время проведения опроса и затраты на него. Входных данных, в обычном понимании, в данной модели нет (возможность отсутствия входных данных – особенность имитационного моделирования).
Сначала требуется определить параметры модели. Пусть а – интервал между появлениями прохожих, которым можно задать вопрос; b – продолжительность беседы; с – желание прохожего беседовать.
Параметры данной модели являются случайными переменными. Случайной переменной назовем переменную, которая в результате опыта со случайным исходом принимает то или иное значение. Возможные значения случайной переменной образуют множество ее значений. В нашей модели а, b, с – случайные переменные. Следующий этап – получение информации для построения модели. Во многих случаях это можно сделать, проведя эксперимент. Предположим, что при сборе информации для каждой переменной изучены 100 прохожих и получены следующие данные.
Интервал между появлениями прохожих, которым можно задать вопрос, был от 0 до 5 минут. Так как строится дискретная модель, то необходимо непрерывный промежуток времени [0;5] сделать дискретным – решить, какие промежутки времени будут использоваться. Например, 1 минута. Это означает, что переменная а может принимать значения 0,1,2,3,4 и 5 мин. Это значения переменной а. Очевидно, что при сборе данных нет необходимости измерять время появления очередного прохожего с точностью, большей, чем 1 мин. Пусть 0 мин. прошло между появлениями 20 прохожих, 1 мин. – между 25 прохожих и т.д.
Таблица 23
| Время между появлениями прохожих, а | Число Прохожих, d(a) | Сумма прохожих | Вероятность | Случайные числа |
| 0,2 | 0-19 | |||
| 0,25 | 20-44 | |||
| 0,34 | 45-78 | |||
| 0,12 | 79-90 | |||
| 0,07 | 91-97 | |||
| 0,02 | 98-99 |
В первом столбце приведены все значения переменной а; во втором – экспериментально полученное число прохожих, прошедших с интервалом а; в третьем – число прохожих, прошедших с интервалом не больше, чем а; в четвертом – вероятность появления прохожего в течение времени а. (Вероятность появления равна отношению числа благоприятных случаев к общему числу случаев). P(a)=d(a)/100. Пусть из 100 прохожих согласились побеседовать 50. Тогда вероятность того, что некоторый прохожий ответит на вопрос, равна 0,5.
Таблица 24
| Согласие прохожих беседовать | Количество прохожих | Сумма прохожих | Вероятность | Случайные числа |
| Да | 0,5 | 0-49 | ||
| Нет | 0,5 | 50-99 |
Предположим, что беседа с прохожими продолжалась от 2 до 8 мин. Следовательно, переменная b изменяется в интервале [2,8] . Будем использовать для b следующие значения: 2,4,6,8.
Таблица 25
| Продолжительность беседы, b | Количество бесед, d | Сумма бесед | Вероятность | Случайные числа |
| 0,2 | 0-19 | |||
| 0,4 | 20-59 | |||
| 0,36 | 60-95 | |||
| 0,04 | 96-99 |
Сбор информации закончен.
Для оценки полученной модели будем использовать математематическое ожидание и дисперсию.
М[a]=0*0.2+1*0.25+2*0.34+3*0.12+4*0.07+5*0.02=1.67
Мат. Ожидание переменной а равно1,67. Следовательно, среднее время между появлениями прохожих – 1,67 мин.
Математическое ожидание переменной b: М[b]=2*0.2+4*0.4+6*0.36+8*0.04=4.48
Следовательно, средняя продолжительность беседы с прохожим – 4,48 мин.
Дисперсия случайной переменной характеризует разброс случайной переменной вокруг математического ожидания. 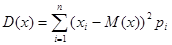 или более просто :
или более просто : 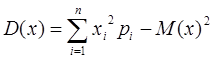
Найдем дисперсию случайных переменных а и b:
D[a]=02*0.2+12*0.25+22*0.34+32*0.12+42*0.07+52*0.02-1.672=1.5211
D[b]= 22*0.2+42*0.4+62*0.36+82*0.04-4.482=2.6496
Следующий этап – моделирование процесса опроса. Пусть имеется генератор случайных чисел, который позволяет получить псевдослучайные числа, равномерно распределенные в заданном диапазоне.
Предположим, имеются случайные числа в диапазоне от 0 до 99. Поставим в соответствие каждой переменной модели набор случайных чисел. Набор случайных чисел определяется вероятностями. Например, для переменной а – интервала между появлениями прохожих – вероятность р(0) = 0,2, т.е. 20% случайных чисел должны соответствовать а=0. Пусть это числа0,1,2 ….19. Аналогично определены остальные случайные числа.
Таблица 26
| № прохожего | Появление прохожего | Согласие беседовать | Беседа | № бесе ды | ||||||
| Случай ное число | Время между появлени ями прохожих ,а | Абсолют ное время появления | Случай ное число | Согла сие беседо вать | Случай ное число | Продол жит. беседы, b | Абс. время оконч. беседы | |||
| Да | ||||||||||
| Да(з) | ||||||||||
| Да | ||||||||||
| Нет(з) | ||||||||||
| Да | ||||||||||
| Нет(з) | ||||||||||
| Нет(з) | ||||||||||
| Да(з) | ||||||||||
| Нет | ||||||||||
| Да | ||||||||||
| Да(з) | ||||||||||
| Нет(з) | ||||||||||
| Да(з) | ||||||||||
| да |
Получим 5 интервью. Пусть получены три последовательности случайных чисел:
56,90,90,87,95,52,11,46,80,1,49,2,65,79;
47,48,9,98,40,55,91,24,82,0,48,96,26,8;
51,87,78,33,65,94,2,79,60,70,68,80,72,86.
Первую используем для определения времени появления прохожих, вторую – для определения согласия прохожих беседовать, а третью – для определения продолжительности беседы.
Предположим, что следующая беседа может начаться сразу после окончания предыдущей. Первое случайное число 56, оно соответствует а=2, следовательно, первый прохожий появится через 2 мин. Второе случайное число 90 показывает, что второй прохожий появится через 3 мин., третий тоже через 3 мин. Случайное число 47 означает, что первый прохожий согласился побеседовать. Случайные числа 48 и 9 означают, что второй и третий прохожий также согласны беседовать. Случайное число 51 показывает, что беседа с первым прохожим продлится 4 мин., следовательно, беседа со вторым прохожим не состоится, т.к. в момент его появления происходит беседа с первым. Можно побеседовать только с третьим прохожим, случайное число 78 показывает, что беседа с ним продлится 6 мин.
Если считать, что процесс начался в начальный момент времени, то в четвертом столбце таблицы указано через, сколько минут после начала процесса появился очередной прохожий.
Чтобы полученные данные были достоверными, проведем 100 экспериментов (бесед).
Составим словесный алгоритм моделирования опроса:
1. Ввод числа бесед.
2. Увеличение счетчика числа прохожих num_peo на 1.
3. Получение случайного числа rnd1.
4. Если 0<=rnd1<=19, то время появления прохожего a=0 мин. ; если 20<=rnd1<=44, тоа=1мин. ; 45<= rnd1<=78, то а=2мин.; 79<= rnd1<=90,то 3мин.; 91<= rnd1<=97, то а=4мин.; 98<= rnd1<=99, то а=5мин.
5. Изменение счетчика абсолютного времени появления прохожего abs_a=abs_a+a.
6. Проверка: если опрашивающий свободен, т.е. абсолютное время появления прохожего больше абсолютного времени окончания беседы abs_a>=abs_b, то переход к шагу 7, в противном случае переход к шагу 12.
7. Получение случайного числа rnd. Если rnd <=49, то прохожий согласен беседовать с=да и увеличение счетчика числа бесед num_int на 1. В противном случае с=нет.
8. Если с=нет, то переход к шагу 12. В противном случае получение случайного числа rnd2 и переход к шагу 9.
9. Если 0<= rnd2<=59, то b=4мин.; если 60<= rnd2<=95,то b=6мин.; если 96<= rnd2<=99, то b=8.
10. Увеличение счетчика чистого времени бесед с прохожими tot_int на время последней беседы: tot_int=tot_int+b.
11. Увеличение счетчика абсолютного времени окончания беседы abs_b на время последней беседы: abs_b=abs_b+b.
12. Проверка, что проведено нужное количество бесед: если num_int<n, то переход к шагу 2, в противном случае переход к шагу 13.
13. Вывод результатов: число прошедших людей num_peo, число проведенных бесед num_int, чистое время бесед tot_int , время появления последнего прохожего abs_a, время окончания последней беседы abs_b.
Если выполнить процедуру моделирования по этой программе для числа бесед 100,200, 300, 500 и 1000 числа бесед, то получим следующий результат.
Таблица 27
| Число прошедших прохожих | Время появления последнего прохожего | Число бесед | Чистое Время бесед | Время окончания последней беседы | M[a] | M[b] |
| 1,564 | 4,32 | |||||
| 1,711 | 4,56 | |||||
| 1,638 | 4,567 | |||||
| 1,668 | 4,52 | |||||
| 1,668 | 4,442 |
Из таблицы видно, что для проведения 100 бесед требуется 638 мин. (11 часов), из них 432 (7 часов) затрачивается на сами беседы, а 206 мин. (3 часа 30 мин.) на ожидание очередного прохожего, согласного беседовать. За 11 часов проходит 404 прохожих.
В алгоритме присутствуют случайные переменные, поэтому если выполнить моделирование еще раз, то результат будет отличаться от предыдущего.
Следующий этап работы с полученной моделью – оценка ее надежности. Необходимо определить насколько модель соответствует реальному процессу. Определим числовые характеристики распределений случайных переменных и сравним их с имеющимися. Так, распределение времени между появлениями прохожих имеет мат.ожидание M[a]=1,67 и дисперсию D[a]=1,5211. Назовем их теоретическими характеристиками. Если характеристики модели близки к теоретическим, то модель надежна. Естественной оценкой для мат.ожидания M[a] является среднее арифметическое результатов экспериментов. M[a]= 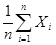 . Дисперсия равняется:
. Дисперсия равняется: 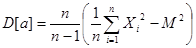
Найдем оценки для математического ожидания распределений случайных переменных a и b , использованных в построенной модели. Для этого в алгоритм добавим шаг, в котором вычислим среднее арифметическое всех значений переменных a и b. Для а – времени между появлениями прохожих – достаточно разделить абсолютное время появления последнего прохожего на количество прохожих., т.е. данные 2-го столбца разделить на данные 1-го столбца таблицы. Результат – оценка для мат.ожидания времени появления записан в таблицу. Аналогично оценка для мат. ожидания переменной b – продолжительности беседы- среднее арифметическое продолжительности проведенных бесед. Достаточно данные 4-го столбца разделить на данные 3-го столбца. Результат записан в 7-м столбце.
Сравним полученные оценки и теоретические характеристики. Найдем относительную погрешность переменных а и b :
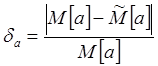 ;
; 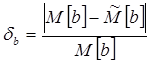


Для 100 бесед: или 6,3%.


Для 200 бесед: 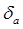 = 2,5%,
= 2,5%, 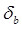 = 1,8%
= 1,8%
Для 300 бесед: 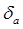 = 1,9%,
= 1,9%, 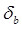 = 1,9%
= 1,9%
Для 500 бесед: 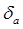 = 0,1%,
= 0,1%, 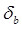 = 0,9%
= 0,9%
Для 1000 бесед: 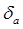 = 0,1%,
= 0,1%, 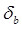 = 0,8%
= 0,8%
Если достаточно, чтобы погрешность модели не превышала 6,5%, то приведенные эксперименты по построенной модели удовлетворительны.
Дата добавления: 2019-04-03; просмотров: 614;
