Конечное вероятностное пространство

Пусть производится некоторый опыт (эксперимент), который имеет конечное число возможных исходов 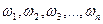. В этом случае 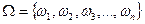(или коротко 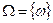- конечное пространство, S - алгебра событий, состоящая из всех (их 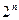) подмножеств множества Ω.

Каждому элементарному событию 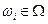, 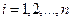поставим в соответствие число 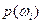, которое назовем вероятностью элементарного события, т.е. зададим на Ω, числовую функцию, удовлетворяющую двум условиям:

1) условие неотрицательности: 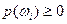для любого ;

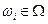2) условие нормированности: .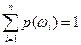

Вероятность Р(А)для любого подмножества А 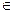Ω определим как сумму

,

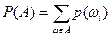(1.8)

т.е. вероятностью Р(А)события А назовем сумму вероятностей элементарных событий, составляющих событие А. Введенная таким образом вероятность удовлетворяет аксиомам Колмогорова (А1-А3).

, ,

,

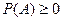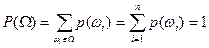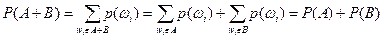если 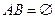, т.е. А и В – два несовместных события. Так как определенная тройка 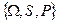есть конечное вероятностное пространство, называемое «дискретным вероятностным пространством».

Частным случаем определения вероятности (1.8) является классическое определение вероятности, когда все исходы опыта равновозможны: 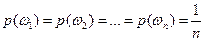(следует из условия нормированности: 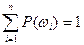). Формула (1.8) примет вид:

,

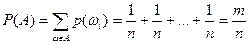т.е. 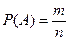, где m – число элементарных событий, образующих событие А (т.е. m – число случаев, благоприятствующих появлению события А).