Геометрическое представление математических моделей

Наглядно можно представить себе только одномерную и двухмерную поверхности отклика, причем в последнем случае удобно пользоваться топографическим способом изображения рельефа поверхности с помощью линий уровня (изолиний), построенных в двумерном факторном пространстве Х. (Рис. 1.4).

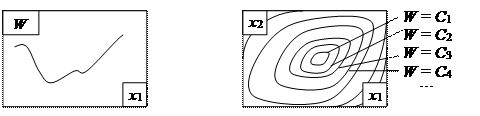Рис. 1.4

Область, в которой определена поверхность отклика, называется областью определения Х*.

Эта область составляет, как правило, лишь часть полного факторного пространства Х (Х* Ì Х) и выделяется с помощью ограничений, наложенных на управляющие переменные x_i , записанных в виде равенств

x_i = C_i , i = 1,…, m;

f_j(x) = C_j , j = 1,…, l

или неравенств

x_{i min} £ x_i £ x_{i max} , i = 1,…, k;

f_j(x) £ C_j , j = 1,…, n,

При этом функции f_j(x) могут зависеть как одновременно от всех переменных, так и от некоторой их части.

Ограничения типа неравенств характеризуют или физические ограничения на процессы в изучаемом объекте (например, ограничения температуры), или технические ограничения, связанные с условиями работы объекта (например, предельная скорость резания).

Возможности исследования моделей существенно зависят от свойств (рельефа) поверхности отклика, в частности, от количества имеющихся на ней «вершин» и ее контрастности.

Количество вершин (впадин) определяет модальность поверхности отклика.

Если в области определения на поверхности отклика имеется одна вершина (впадина), модель называется унимодальной.

Характер изменения функции при этом может быть различным (Рис. 1.5).

W		W		W
	x* x		x* x		x* x

а б в

Рис. 1.5

Модель может иметь разрывы первого рода (см. рис. 1.5. а). Непрерывная унимодальная модель может иметь точки разрыва производной – разрывы второго рода (см. рис. 1.5. б). На рис. 1.5 в показана непрерывно-дифференцируемая унимодальная модель.

Для всех трех случаев, представленных на рис. 1.5, выполняется общее требование унимодальности:

Если W(x*) = extr W, то из условия х₁ < x₂ < x* (x₁ > x₂ > x*) следует
W(x₁) < W(x₂) < W(x*) , если extr – максимум, или W(x₁) > W(x₂) > W(x*) , если extr – минимум, то есть, по мере удаления от экстремальной точки значение функции W(x) непрерывно падает (растет).

Наряду с унимодальными бывают полимодальные модели (Рис. 1.6).

Рис. 1.6

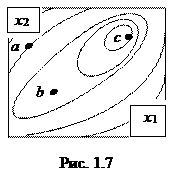Другим важным свойством поверхности отклика является ее контрастность, показывающая чувствительность результирующей функции к изменению факторов. Контрастность характеризуется величинами производных. Продемонстрируем характеристики контрастности на примере двумерной поверхности отклика (Рис. 1.7). Точка а расположена на «склоне», характеризующем равную контрастность по всем переменным х_i (i=1,2); точка b расположена в «овраге», в котором различная контрастность по различным переменным (имеем плохую обусловленность функции); точка с расположена на «плато», на котором низкая контрастность по всем переменным х_i говорит о близости экстремума.